定义

拓扑空间X称为是 连通 的。当且仅当以下叙述之一成立：

X不能表示为两个不相交的非空开集的并集。

∀A⊆X，A≠X或∅，A ∩(X-A) ≠∅。

一个拓扑空间被称为是 不连通 的，若它不是连通的。

连通性是拓扑空间的一个拓扑不变性质，即两个拓扑空间之间若存在一个同胚映射，其中一个空间是连通的，则另一个空间也是连通的。

一些数学家承认空集(按照它独有的拓扑)是连通空间，不过也有数学家不承认这一点。

连通单元

每个空间都能表成它的连通单元的不相交并集。

连通单元必然是闭的，在够好的空间（如流形、代数簇）上也同时是开的，但并非总是如此。

其它连通性定义

道路连通，弧连通

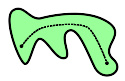
 R ² 的这个子空间是道路连通的，因为在这个空间的任何两点之间可绘制一个道路。

道路连通空间是连通空间，反之不一定。

道路连通的豪斯多夫空间必为弧连通空间。

局部连通

拓扑空间X称为 局部连通 的，当且仅当以下叙述之一成立：

空间中的任一点都存在连通的邻域（即该邻域是X的连通子集）。

空间的拓扑基完全由连通的集合组成。

例子

拓扑学家的正弦曲线 。在平面欧几里得空间 R 2 {\displaystyle \mathbb {R} ^{2}} 中定义集合 S = { ( x , sin ⁡ ⁡ --> 1 x ) | x ∈ ∈ --> ( 0 , 1 ] } {\displaystyle S=\{(x,\sin {\frac {1}{x}})|x\in (0,1]\}} 和 T = { ( 0 , y ) | y ∈ ∈ --> [ 0 , 1 ] } {\displaystyle T=\{(0,y)|y\in [0,1]\}} 。考虑 S ∪ ∪ --> T {\displaystyle S\cup T} 在 R 2 {\displaystyle \mathbb {R} ^{2}} 中诱导的子拓扑空间，它是连通的，但不是局部连通的。

有理数集上的连通单元都是单元素集合，所以有理数集是一个完全不连通空间。

参考文献

Munkres, James R. Topology, Second Edition. Prentice Hall. 2000. ISBN 0-13-181629-2.

MathWorld上 Connected Set 的资料，作者：埃里克·韦斯坦因。

V. I. Malykhin,Connected space, (编) Hazewinkel, Michiel,数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4

Muscat, J; Buhagiar, D.Connective Spaces (PDF) . Mem. Fac. Sci. Eng. Shimane Univ., Series B: Math. Sc. 2006, 39 : 1–13. .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。