性质理论

根据热力学的理论，物质会寻求存在于最低能量的状态，而关键便是个可以减少化学能的办法。水是极性物质，并因此可以在内部形成氢键，这使得它有许多独别的性质。但是，因为疏水物不是电子极化性的，它们无法形成氢键，所以水会对疏水物产生排斥，而使水本身可以互相形成氢键。这即是导致 疏水作用 （这名称并不正确，因为能量作用是来自亲水性的分子 ）的疏水效应，因此两个不相溶的相态（亲水性对疏水性）将会变化成使其界面的面积最小时的状态。此一效应可以在相分离的现象中被观察到。

超疏水性

超疏水性物质，如荷叶，具有极难被水沾湿的表面，其水在其表面的接触角超过150°，滑动角小于20°。

理论

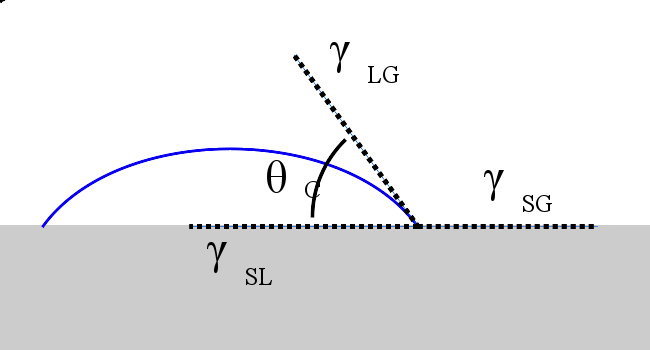
气体环绕的固体表面的液滴。接触角θ C ，是由液体在三相（液体、固体、气体）交点处的夹角。

1805年，托马斯·杨通过分析作用在由气体环绕的固体表面的液滴的力而确定了接触角θ。

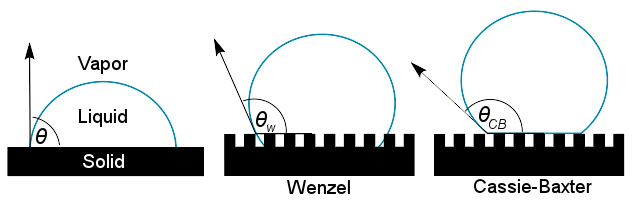
气体环绕的固体表面的液滴，形成接触角θ。如果液体与固体表面微结构的凹凸面直接接触，则此液滴处于Wenzel状态；而如果液体只是与微结构的凸面接触，则此液滴处于Cassie-Baxter状态。

θ可以用接触角测量计来测量。

Wenzel确定了当液体直接接触微结构化的表面时，θ角会转变为 θ θ --> W ∗ ∗ --> {\displaystyle \theta _{W}*}

其中，r为实际面积与投影面积的比率。 Wenzel的方程显示了微结构化一个表面将会放大表面张力。疏水性表面（具有大于90°的接触角）在微结构化之后会变得更加疏水，其新的接触角将比原来增大。然而，一个亲水性表面（具有小于90°的接触角）在微结构化之后却会变得更加亲水，其新的接触角将比原来减小。

Cassie和Baxter发现如果液体悬浮在微结构表面，θ角将会变为 θ θ --> C B ∗ ∗ --> {\displaystyle \theta _{CB}*}

其中，φ为固体与液体接触面积的比例。 在Cassie-Baxter状态下的液体比Wenzel状态下更具有运动性。

通过用以上两个方程计算出的新接触角，我们可以预测Wenzel状态或Cassie-Baxter状态是否应该存在。由于有自由能最小化的限制，预测出具有更小的新接触角的状态就会更可能存在。从数学上来说，要使Cassie-Baxter状态存在，以下的不等式必须成立。

最近提出的一个判断Cassie-Baxter状态是否存在的替代标准是：1)接触线力克服液滴未被支撑部分的重力；2)微结构足够高从而阻止液滴接触微结构的基底（即凹面）。

接触角是静态测量疏水性的方法，接触角滞后和滑动角则对疏水性的动态测量法。接触角滞后是一种鉴定表面异质性的现象。 当移液器将液体注到固体表面时，液体就会形成一定的接触角。随着注入液体的增加，液滴的体积会随之增加，接触角也会变大，但三相边界会保持固定直到液体突然溢出。在液体溢出前瞬间的接触角被称为前进接触角。回退接触角可以通过将液体从液滴中吸出来测量。随着液体被吸出，液滴的体积减小，接触角也减小，但三相边界同样保持固定直到被完全吸回。在液体被吸回瞬间的接触角被称为回退接触角。而前进接触角和回退接触角之间的差异就是接触角滞后，它被用来鉴定表面的异质性、粗糙性和运动性。非同质的表面会有能够阻碍接触线的区域。滑动角是另一种动态测量疏水性的方法：在固体表面放置一个液点，倾斜表面直到液滴开始滑动，此时的倾斜角即为滑动角。处于Cassie-Baxter状态的液滴通常会表现出比Wenzel状态更小的滑动角和接触角滞后。

研究和应用

纳米纤维表面的水珠

许多在自然界中找到的超疏水性物质都遵循Cassie定律，而它在次微米尺度下可以和空气组成双相物质。莲花效应便是基于此一原理而形成的。仿生学上，超疏水性物质的例子有利用奈米科技制作的nanopin膜（nanopin film）。

另见

亲水性

两性分子

浸润

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。