性质

面的图形：正方形 面的数目：6 边的数目：12 顶点数目：8 表面积： 6 a 2 {\displaystyle 6a^{2}\ } 体积： a 3 {\displaystyle a^{3}\ } 二面角角度： 90 ∘ ∘ --> {\displaystyle 90^{\circ }} 外接球半径： 3 4 a {\displaystyle {\sqrt {\frac {3}{4}}}a} ≈ ≈ --> 0.866 a {\displaystyle \approx 0.866a} 内接球半径： a 2 {\displaystyle {\frac {a}{2}多面体 对偶多面体：正八面体 在所有表面积一定的长方体中，立方体的体积最大，同样，在所有线性大小（长宽高之和）一定的长方体中，立方体的体积也是最大的。反过来，体积相等的长方体中，立方体拥有最小表面积和线性大小。

正交投影

我们可以从不同角度将立方体投影到二维平面上，这些投影都各自携带有立方体原本BC 3 对称性的一部分。

顶点坐标及表面方程

在三维直角坐标系中，对于以原点为中心的、各棱平行于坐标轴的、棱长为2的立方体，其顶点坐标为 (±1, ±1, ±1) 的全排列。它包含了所有满足|x|≤1且|y|≤1且|z|≤1的点(x,y,z)。 在R 中，以点(x 0 ,y 0 ,z 0 )为中心的立方体表面是点(x,y,z)的运动轨迹，其中x,y,z满足：

半正对称性与表面涂色

作为正多面体之一，立方体拥有较高的对称性，它的所有面在几何上都是相同的，不可区分的。可是我们也可以想象将立方体的面“涂上”不同的“颜色”，使它其的不同面拥有不同的“几何意义”，使立方体拥有不同的对称性。在立方体完全的对称性，即正八面体对称性O h 中，立方体的所有面都是相同的。二面体对称性D 4h 则将立方体描述得像一个正四棱柱，有两个颜色相同的上下底面，其余4个侧面颜色相同。立方体最低的对称性D 2h 也将立方体描述的像一个棱柱，不过是长方形棱柱，即一个长方体，它的相对的面颜色相同，而相邻的面是不同的。每一种半正对称性都有自己的施莱夫利符号、 考克斯特-迪肯符号 （ 英语 ： Coxeter-Dynkin digram ） 和 Wythoff符号 （ 英语 ： Wythoff symbol ） 。此外，由于其对偶正八面体也可被看作是正三反棱柱，立方体也可被看作是正三反棱柱的对偶，即正三偏方面体。

几何性质

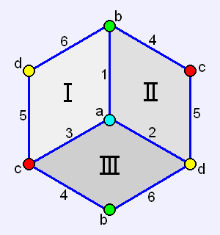
立方体有11种不同的展开图，即是说，我们可以有11种不同的方法切开空心立方体的7条棱而将其展平为平面图形，见右图。

  立方体的11种不同展开图

如果我们要将立方体涂色而使相邻的面不带有相同的颜色，则我们至少需要3种颜色（类似于四色问题）。 立方体是唯一能够独立密铺三维欧几里得空间的柏拉图正多面体，因此立方体堆砌也是四维唯一的正堆砌（三维空间中的堆砌拓扑上等价于四维多胞体）。它又是柏拉图立体中唯一一个有偶数边面——正方形面的，因此，它是柏拉图立体中独一无二的环带多面体（它所有相对的面关于立方体中心中心对称）。 将立方体沿对角线切开，能得到6个全等的正4棱柱（但它不是半正的，底面棱长与侧棱长之比为2:√3）将其正方形面贴到原来的立方体上，能得到菱形十二面体(Rhombic Dodecahedron)（两两共面三角形合成一个菱形）。

与其他形状的关系

将立方体的其中四个顶点相连，而这四个顶点任何两条都没有落在立方体同一条的边上，可得到一个正四面体，其边长为立方体边长的 2 {\displaystyle {\sqrt {2}}} ，其体积为立方体体积的 1 3 {\displaystyle {\frac {1}{3}}} 。

  正四面体外接正六面体

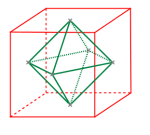
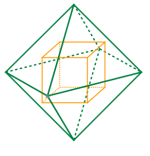
立方体的对偶多面体是正八面体。

当正八面体在立方体之内： 正八面体体积 : 立方体体积 =[(1/3)×高×底面积]×2 : 边 =(1/3)(n/2)[(n )/2]2 : n =1 : 6

星形八面体的对角线可组成一个立方体。

截半立方体：从一条棱斩去另一条棱的中点得出

截角立方体

超正方体：立方体在高维度的推广。更加一般的，立方体是一个大家族，即立方形家族（又称超方形、正测形）的3维成员，它们都具有相似的性质（如二面角都是90°、有类似的超体积公式，即V n-cube =a 等）。

长方体、偏方面体的特例。

相关多面体

将立方体 对映映射 （ 英语 ： Antipodal point ） 后的到的商形成的一个实射影多面体，即 Hemi-立方体 （ 英语 ： Hemicube ） (hemicube) （不应叫其“半立方体”，因为其易与‘demicube’混淆）。

  Hemi-立方体是立方体2到1的商

正方体的对偶多面体是正八面体，如果原正方体棱长为1，则对偶正八面体棱长为√2。 正方体是一种最特殊的四边形正六面体：

立方体的8个顶点可以被交错地分为两组，每一组都构成一个完整的正四面体，更严格地说，这是作为 半(Demi-)立方体 （demicube）的正四面体。这两个正四面体组合到一起，就构成了一个正的复合多面体—— 星形正八面体(Stella Octagula) 。两个正四面体重合的地方构成凸的正八面体。这意味着，正四面体的对称群A 3 是正方体对称群的子群，对应着能将半立方体变换到自身的对称变换，立方体其余的对称变换能将两个半立方体变换到对方。一个这样的正四面体占据了立方体体积的 / 3 ,立方体剩余的部分是4个全等的、顶角是立方体立体角的正三棱锥，各占立方体体积的 / 6 。 从立方体各棱中点处切掉立方体的角，我们会发现原先立方体的正方形面变成了其对偶的正方形面，而切掉的顶点处出现了新的正三角形面，这样的操作叫“截半”(Rectification)，得到的半正多面体叫截半立方体(Rectified Cube)，又叫立方八面体(Cuboctahedron)。如果我们不在棱中点处截它，则这种操作叫“截角”(Truncation)，正方形面变成了八边形。如果截的合适，则我们可将正方形截成正八边形，得到的半正多面体叫截顶立方体(Truncated Cube)。如果我们同时截掉立方体的棱和顶，则这种操作叫“截棱”(Centellation)，如果截的恰当，得到的半正多面体是小斜方截半立方体(Rhombicuboctahedron)。

正十二面体有20个顶点，它们可以以不同组合分成由8个顶点组成的5组，这8个顶点两两相连，构成内接在正十二面体内部的立方体，它的棱都是正十二面体的各面的对角线。这五个立方体组合在一起，构成复合多面体——五复合立方体。

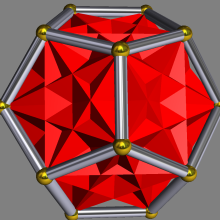
  正十二面体内部的五复合立方体

如果我们完全切掉立方体相对的两个顶点，我们会得到一个非正的八面体，将8个这样的八面体正三角形面对正三角形面贴到正八面体上，则我们得到截半立方体。 立方体与所有其它拥有BC 3 对称性的多面体（如正八面体和立方八面体）构成正八面体家族：

此外，立方体在拓扑上与其它3阶正镶嵌{n,3}相关：

立方体在拓扑上还和其它阶的正方形正镶嵌{4,n}(n≥3)有关：

立方体是正四棱柱：

应用

日常生活

游戏

视错觉

数论

数学问题

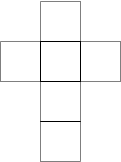
  由正方体展开图可得知正方体表面积算法

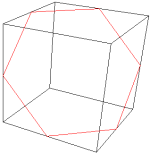
  正六边形的切法：沿上底两条邻边的中点，切至下底两条邻边的中点

体积与表面积

体积=长×宽×高=边

表面积=每个面面积×6=边 ×6

倍立方体问题

参见尺规作图，已经证明此题无法用无刻度的直尺与圆规去画出 2 3 {\displaystyle {\sqrt[{3}]{2}}} 的位置

最大的横切面

立方体的横切面只有四种：

三角形

矩形

五边形

六边形

其中以正六边形的面积最大,若立方体的棱长为a,则正六边形的面积为 3 3 a 2 4 {\displaystyle {\frac {3{\sqrt {3}}a^{2}}{4}}} 。

参见

四角柱

超方形

正八面体

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。