定义

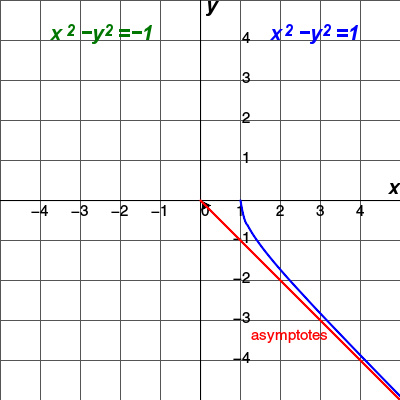
共轭单位直角双曲线

前两个上面已经列出了：

平面切直角圆锥面的两半的交截线。

与两个固定点（称为 焦点 ）距离差为常数的点的轨迹。

到一个焦点的距离和到一条直线（称为 准线 ）的距离的比例是大于 1 {\displaystyle 1} 的常数的点的轨迹。这个常数称为双曲线的偏心率。

双曲线由分开两个焦点的两个分离的称为臂或分支的曲线构成。随着到焦点的距离的变大，双曲线就越逼近称为渐近线的两条线。渐近线交叉于双曲线的中点，并对于东西开口的双曲线有斜率 ± ± --> b a {\displaystyle \pm {\frac {b}{a}}} ，对于北南开口的双曲线有斜率 ± ± --> a b {\displaystyle \pm {\frac {a}{b}}} 。

双曲线有个性质，出自一个焦点的射线反射于双曲线后看起来像是出自另一个焦点。

双曲线的一个特殊情况是“等轴”或“直角”双曲线，它的渐近线交于直角。以坐标轴作为渐近线的直角双曲线由方程 x y = c {\displaystyle xy=c} 给出，这里的 c {\displaystyle c} 是常数。

如同正弦和余弦函数给出椭圆的参数方程，双曲函数给出双曲线的参数方程。

如果对双曲线方程交换 x {\displaystyle x} 和 y {\displaystyle y} ，得到它的共轭双曲线。共轭双曲线有同样的渐近线。

笛卡尔坐标

中心位于 ( h , k ) {\displaystyle (h,k)} 的左右开口的双曲线：

中心位于 ( h , k ) {\displaystyle (h,k)} 的上下开口的双曲线：

实轴贯穿双曲线的中心并交双曲线两臂于它们的顶点（拐点）。焦点位于双曲线实轴的延长线上。虚轴贯穿双曲线中点并垂直于实轴。

在两个公式中， a {\displaystyle a} 是半实轴（在双曲线两臂之间沿着实轴测量的距离），而 b {\displaystyle b} 是半虚轴。

如果用双曲线的两个顶点的切线交渐近线形成一个矩形，在切线上的两边的长度是 2 b {\displaystyle 2b} ，平行于实轴的两边的长度是 2 a {\displaystyle 2a} ，注意 b {\displaystyle b} 可以大于 a {\displaystyle a} 。

如果计算从双曲线上任意准线上的点到每个焦点的距离，这两个距离的差的绝对值总是 2 a {\displaystyle 2a} 。

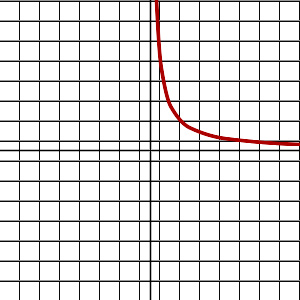
直角双曲线 y = 1 x {\displaystyle y={\tfrac {1}{x}}} 的图像。

离心率给出自：

左右开口的双曲线的焦点是： ( h ± ± --> c , k ) {\displaystyle \left(h\pm c,k\right)} ，其中c给出自 c 2 = a 2 + b 2 {\displaystyle c^{2}=a^{2}+b^{2}} 。

上下开口的双曲线的焦点是： ( h , k ± ± --> c ) {\displaystyle \left(h,k\pm c\right)} ，其中c给出自 c 2 = a 2 + b 2 {\displaystyle c^{2}=a^{2}+b^{2}} 。

对于以直线 x = h {\displaystyle x=h} 和直线 y = k {\displaystyle y=k} 为渐近线的直角双曲线：

这种双曲线最简单的例子是：

极坐标

左右开口的双曲线：

上下开口的双曲线：

上右下左开口的双曲线：

上左下右开口的双曲线：

在所有公式中，中心在极点，而 a {\displaystyle a} 是半实轴和半虚轴。

双曲线的参数方程

左右开口的双曲线：

或

上下开口的双曲线：

或

在所有公式中， ( h , k ) {\displaystyle (h,k)} 是双曲线的中点， a {\displaystyle a} 是半实轴而 b {\displaystyle b} 是半虚轴。

双曲线的标准方程

焦点在 x {\displaystyle x} 轴： x 2 a 2 − − --> y 2 b 2 = 1 {\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}

焦点在 y {\displaystyle y} 轴： y 2 a 2 − − --> x 2 b 2 = 1 {\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}

双曲线的渐近线方程

焦点在 x {\displaystyle x} 轴： y = ± ± --> b a x {\displaystyle y=\pm {\frac {b}{a}}x}

焦点在 y {\displaystyle y} 轴： y = ± ± --> a b x {\displaystyle y=\pm {\frac {a}{b}}x}

圆锥曲线方程

ρ ρ --> = e p 1 + e cos ⁡ ⁡ --> θ θ --> {\displaystyle \rho ={\frac {ep}{1+e\cos \theta }}}

当 e > 1 {\displaystyle e>1} 时，表示双曲线。其中 p {\displaystyle p} 为焦点到准线距离， θ θ --> {\displaystyle \theta } 为弦与 x {\displaystyle x} 轴夹角。

参考文献

参见

圆锥曲线

双曲函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。