工作内涵业务的工作，通常包括售前咨询与售后服务，其具体项目包括销售管理、客户名单收集、潜在客户的筛选与连络、公司服务/产品的推介、报价、与客户互动、持续追踪进度等一切确保销售流程顺畅的手段。在其他语言中的相同用法业务与“企业”一词类似并且有所关联，在与信息技术应用或企业信息化相关的许多新概念中，业务与英文中的Business对应，贴近其某部分特定的含义，例如：业务流程或业务过程（businessprocess）、业务流程管理（businessprocessmanagement,BPM）、业务流程再造（businessprocessreengineering,BPR）、业务流程建模（businessprocessmodeling）、业务集成（businessintegration）、业务分析师（businessanalyst）等等。当"业务（business）"在这种用法中，指的是组织中有目...

参考文献参见RNA

工作对上级提供意见:业务部门应该随时把实际的工作情形、所遭遇的困难、执行的利弊得失报告上级长官，以提供决策工作的参考。对业务设计执行。对工作实际进行。对于组织和方法的改进，组织和工作方法更有效率组织要则业务部门应该采取首长制避免委员制，以期事权统一、责任集中。应本机能一致的原则之下，把性质相同的工作完全交由一个部门掌理，以免事权冲突、工作重复。应该采取层级制或系统制的组织，以期指挥灵活、贯彻命令。应该遵守管理经济学原则，首长所直接管辖的工作单位不该过多，已超出能力负荷范围。应该守事权称适的原则，让机关的权利足以负担其责，人员、经费足以应付其业务上的实际需求。确定每个工作人员的权责，实施分层负责和分级授权。负责人条件业务部门负责人选必须兼具通才的管理能力、专业的知能。因为就其所主管的单位而言，一个主管不能不具备通才的管理能力；而就其所主管的专门而言业务，其亦得具备该业务的专门知能。唯二者的比...

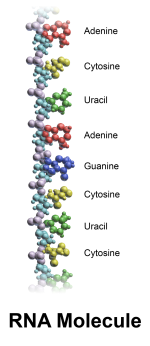
与DNA的比较RNA分子中的含氮碱基50S核糖体亚单位的3D结构示意图。rRNA以土黄色表示，蛋白质以蓝色表示。活性位点为rRNA的一个小片段，以红色标出RNA的分子结构与DNA非常相似，但是，两者有以下三个主要不同点：与DNA相似，大部分有生物活性的RNA，包括mRNA、tRNA、rRNA、snRNA，以及其他一些非编码RNA，虽然是单链，但含有自我互补的序列，能使得它们能进行折叠，形成互补双链接构（茎）。对RNA的分析表明，它们有着相对更复杂的结构。和DNA不同，RNA的二级结构并不是单纯的双螺旋，而由一系列短的二级结构构成。通过这些短的二级结构的组合，RNA甚至可以拥有与蛋白质相似的结构，并像酶那样催化化学反应（这样的RNA被称为核酶）。比如，对核糖体进行分析表明，其催化成肽反应的活性位点完全由RNA构成。结构siRNA（小干扰RNA）中的碱基互补配对（图中省略了氢原子）RNA的单体...

例子纵览线性算子设V和W是向量空间并设T是从V到W的线性变换。如果0W是W的零向量，则T的核是单元素集合{0W}的前像；就是说V的由被T映射到元素0W的那些V的元素构成的子集。核通常指示为“kerT”，或者：因为线性变换保持零向量，V的零向量0V必须属于核。变换T是单射的，当且仅当它的核只是单元素集合{0V}。kerT显然总是V的子空间。因此，它使谈论商空间V/(kerT)有意义。对向量空间的第一同构定理声称这个商空间自然同构于T的像（它是W的子空间）。作为结论，V的维度等于核的维度加上像的维度。如果V和W是有限维的向量空间，并且基已经选择好了，则T可以用矩阵M描述，而这个核可以通过解齐次线性方程组Mv=0来计算。在这种表示中，核对应于M的零空间。零空间的维度叫做M的零化度（nullity）由M的纵列数减去M的秩得到，这是秩-零化度定理的结论。解齐次微分方程经常涉及计算特定微分算子的核。例...