定义

数学上的证明包括两个不同的概念。首先是非形式化的证明：一种以自然语言写成的严密论证，用来说服听众或读者去接受某个定理或论断的真确性。由于这种证明使用了自然语言，因此对于非形式化证明在严谨性上的标准，将取决于听众或读者对课题的理解程度。非形式化证明出现在大多数的应用场合中，例如科普讲座、口头辩论、初等教育或高等教育的某些部分。有时候非形式化的证明被称作“正式的”，但这只是强调其中论证的严谨性。而当逻辑学家使用“正式证明”一词时，指的是另一种完全不同的证明——形式化证明。

在数理逻辑中，形式化证明并不是以自然语言书写，而是以形式化的语言书写：这种语言包含了由一个给定的字母表中的字符所构成的字符串。而证明则是一种由该些字符串组成的有限长度的序列。这种定义使得人们可以谈论严格意义上的“证明”，而不涉及任何逻辑上的模糊之处。研究证明的形式化和公理化的理论称为证明论。尽管理论上来说，每个非形式化的证明都可以转化为形式化证明，但实际中很少会这样做。对形式化证明的研究主要应用在探讨关于可证明性的一般性质，或说明某些命题的不可证明性等等。

常见的证明技巧

直接证明

直接证明 （ 英语 ： Direct proof ） 也称为逻辑演绎，是指从公认的事实或者公理出发，运用逻辑推演而导出需要证明的命题的真伪的方法。直接证明法一般使用谓词逻辑，运用存在量词或全称量词。主要的证明方式有肯定前件论式、否定后件论式、假言三段论式以及选言三段论式等等。比如说要证明命题：“任何奇数乘以另一个奇数仍然是奇数”，可以直接证明如下：

构造法

构造法一般用于证明存在性定理，运用构造法的证明称为构造性证明。具体做法是构造一个带有命题里所要求的特定性质的实例，以显示具有该性质的物体或概念的存在性。也可以构造一个反例，来证明命题是错误的 。例如证明命题“2的素数次幂减一后不总是素数”，便可用构造法：

有些构造法证明中并不直接构造满足命题要求的例子，而是构造某些辅助性的工具或对象，使得问题更容易解决。一个典型的例子是常微分方程稳定性理论中的李亚普诺夫函数的构造 。又如许多几何证明题中常常用到的添加辅助线或辅助图形的办法。

非构造性证明

与构造法证明相对的是非构造性证明，即不给出具体的构造而证明命题所要求对象的存在性的证明方法。比如下面例子：

在这个证明里并没有给出使得 x y {\displaystyle x^{y}} 是有理数的两个具体的无理数 。

穷举法

穷举法 （ 英语 ： Proof by exhaustion ） 是一种列举出命题所包含的所有情况从而证明命题的方法 。例如证明“所有两位数中只有25和76的平方是以自己作为尾数”，只需计算所有两位数：10至99的平方，一一验证即可。显然，使用穷举法的条件是命题所包含的可能情况为有限种，否则无法一一罗列。

换质位法

在谓词逻辑里，若同时否定一个命题的主词和谓词，则其结果称为原命题的 换质 。若交换主词和谓词的位置，则其结果被称作 换位 。先换质再换位则被称为 换质位 ，同理先换位再换质则被称为 换位质 。例如“所有的S是P”的换质位是“所有的不是P的不是S”。 换质位法 （ 英语 ： Proof by contrapositive ） 是指利用换质及换位，将一个命题改为一个与其逻辑等价的命题，因此只要证明了后者就证明了原来的命题 。例如，要证明鸽笼原理：“如果n个鸽笼里装有多于n只鸽子，那么至少有一个笼子里有两只或者两只以上鸽子”，可以转证与其等价的逆否命题：“如果n个鸽笼的每一个中至多装有一只鸽子，那么n个鸽笼里至多装有n只鸽子”。而后者是显然的。

个案分析

个案分析或分类讨论，是指将结论分成有限的个案，然后逐个证明的方法。

算两次

算两次是一种对同一个量进行两种虽不同但都正确的分析，得到两个虽不同但相等的表达式的方法，常用于证明恒等式 。

间接证明

反证法

反证法是一种古老的证明方法，其思想为：欲证明某命题是假命题，则反过来假设该命题为真。在这种情况下，若能通过正确有效的推理导致逻辑上的矛盾（如导出该命题自身为假，于是陷入命题既真且假的矛盾），则能证明原来的命题为假。 无矛盾律和排中律是反证法的逻辑基础。反证法的好处是在反过来假设该命题为真的同时，等于多了一个已知条件，这样对题目的证明常有帮助 。

例子：证明命题“ 2 {\displaystyle {\sqrt {2}}} 不是有理数”。

数学归纳法

骨牌一个接一个倒下，就如同一个值到下一个值的过程。

数学归纳法是一种证明可数无穷个命题的技巧。欲证明以自然数 n 编号的一串命题，先证明命题1成立，并证明当命题 n 成立时命题 n +1也成立，则对所有的命题都成立 。在皮亚诺公理系统中，自然数集合的公理化定义就包括了数学归纳法。数学归纳法有不少变体，比如从0以外的自然数开始归纳，证明当命题对小于等于 n 的自然数成立时命题 n +1也成立，反向归纳法，递降归纳法等等。广义上的数学归纳法也可以用于证明一般良基结构，例如集合论中的树。另外，超限归纳法提供了一种处理不可数无穷个命题的技巧，是数学归纳法的推广 。

例子：证明对所有自然数 n {\displaystyle n} ，命题 P ( n ) : 1 2 + 2 2 + 3 2 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 {\displaystyle P(n):\;\;1^{2}+2^{2}+3^{2}+...+n^{2}={\frac {n(n+1)(2n+1)}{6}}}

当n=1，左边=1，右边= P ( 1 ) : 1 ( 1 + 1 ) ( 2 + 1 ) 6 = 1 {\displaystyle P(1):\;\;{\frac {1(1+1)(2+1)}{6}}=1}

假设对某个自然数 k {\displaystyle k} ，命题 P ( k ) {\displaystyle P(k)} 成立： 1 2 + 2 2 + 3 2 + . . . + k 2 = k ( k + 1 ) ( 2 k + 1 ) 6 {\displaystyle 1^{2}+2^{2}+3^{2}+...+k^{2}={\frac {k(k+1)(2k+1)}{6}}} ，以下证明 P ( k + 1 ) {\displaystyle P(k+1)} 成立，即： 1 2 + 2 2 + 3 2 + . . . + k 2 + ( k + 1 ) 2 = ( k + 1 ) ( k + 2 ) ( 2 k + 3 ) 6 {\displaystyle 1^{2}+2^{2}+3^{2}+...+k^{2}+(k+1)^{2}={\frac {(k+1)(k+2)(2k+3)}{6}}} ：

所以，对任意自然数 n {\displaystyle n} ，都有 1 2 + 2 2 + 3 2 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 {\displaystyle 1^{2}+2^{2}+3^{2}+...+n^{2}={\frac {n(n+1)(2n+1)}{6}}}

其他证明方式

直观证明

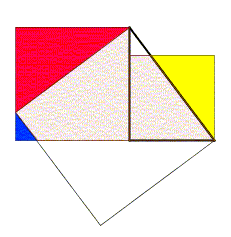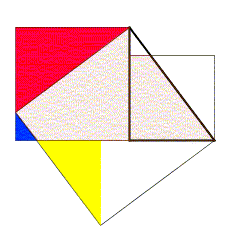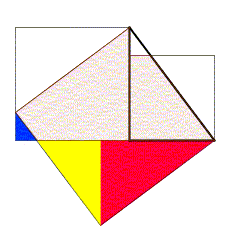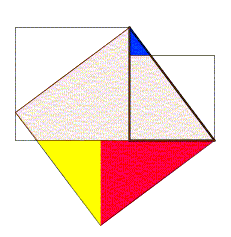
勾股定理的一个图示证明

直观证明或可视化证明是指用图像或表格等直观的手段证明命题的方法。这类证明可以达到不借助语言而证明的效果。如右图是勾股定理的一个图示证明。

计算机辅助证明

电脑协助证明是二十世纪出现的证明方式。直到二十世纪中，人们一直认为任何的数学证明都应当能够被一个水平足够的数学家检验，以证实其正确性。然而，今天的数学家已经能够运用计算机来证明定理，并且完成人类难以做到的计算 。1976年四色定理的证明是计算机辅助证明的经典例子 。证明的方法是将地图上的无限种可能情况减少为1936种状态，并由计算机对每个可能的情况进行验证。有不少数学家对于计算机证明持谨慎态度，因为很多证明太长，不能由人手直接验证。此外，算法上的错误，输入时的失误甚至计算机运行期间出现的错误都有可能导致错误的结果。

证明的结尾

有时在证明的结尾会加上Q.E.D.三个字母，这是拉丁文Quod Erat Demonstrandum的缩写，意思是“证明完毕”。现在的证明完毕符号，通常是 ■ （实心黑色正方形），称之为“墓碑”或“哈尔莫斯（Halmos symbol）”（因保罗·哈尔莫斯最先采用此做法）。墓碑有时是空心的 □ 。另一个简单方法是写“proven”、“shown”或“证毕”之类的文字。

参见

证明论

模型论

自动定理证明

无效证明

Q.E.D.

墓碑符号

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。