其它记法

另一种标记方法是使用艾佛森括号（得名于肯尼斯·艾佛森）：

同时，当一个变量为0时，常常会被略去，记号变为 δ δ -->i{\displaystyle \delta _{i}\,\!} ：

在线性代数中，克罗内克函数可以被看做一个张量，写作 δ δ -->ji{\displaystyle \delta _{j}^{i}\,\!} 。

数字信号处理

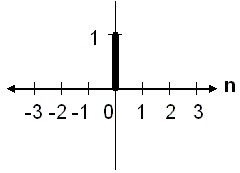
冲激函数

类似的，在数字信号处理中，与克罗内克函数等价的概念是变量为 Z{\displaystyle \mathbb {Z} \,\!} (整数)的函数：

δ δ -->[n]={1,n=00,n≠ ≠ -->0{\displaystyle \delta [n]={\begin{cases}1,&n=0\\0,&n\neq 0\end{cases}}\,\!}。

这个函数代表着一个冲激或单位冲激。当一个数字处理单元的输入为单位冲激时，输出的函数被称为此单元的冲激响应。

性质

克罗内克函数有筛选性：对任意 j∈ ∈ -->Z{\displaystyle j\in \mathbb {Z} \,\!} ：

如果将整数看做一个装备了计数测度的测度空间，那么这个性质和狄拉克δ函数的定义是一样的：

实际上，狄拉克δ函数是根据克罗内克函数而得名的。在信号处理中，两者是同一个概念在不同的上下文中的表现。一般设定 δ δ -->(t){\displaystyle \delta (t)\,\,\!} 为连续的情况（狄拉克函数） ，而使用i, j, k, l, m, and n 等变量一般是在 离散的情况下（克罗内克函数）。

线性代数中的应用

在线性代数中，单位矩阵可以写作 (δ δ -->ij)i,j=1n{\displaystyle (\delta _{ij})_{i,j=1}^{n}\,\!} 。

在看做是张量时（克罗内克张量），可以写作 δ δ -->ji{\displaystyle \delta _{j}^{i}\,\!} 。

这个(1,1)向量表示:

作为线性映射的单位矩阵。

迹数。

内积V∗ ∗ -->⊗ ⊗ -->V→ → -->K{\displaystyle V^{*}\otimes V\to K\,\!} 。

映射 K→ → -->V∗ ∗ -->⊗ ⊗ -->V{\displaystyle K\to V^{*}\otimes V\,\!} ，将数量乘积表示为外积的形式。

广义克罗内克函数

定义广义克罗内克函数为 n× × -->n{\displaystyle n\times n\,\!} 矩阵的行列式，以方程式表达为

其中，δ δ -->ji{\displaystyle \delta _{j}^{i}\,\!} 是个张量函数，定义为 δ δ -->ji =def δ δ -->ij{\displaystyle \delta _{j}^{i}\ {\stackrel {def}{=}}\ \delta _{ij}\,\!} 。

以下列出涉及广义克罗内克函数的一些恒等式：

δ δ -->imnijk=δ δ -->mnjk=δ δ -->mjδ δ -->nk− − -->δ δ -->njδ δ -->mk{\displaystyle \delta _{imn}^{ijk}=\delta _{mn}^{jk}=\delta _{m}^{j}\delta _{n}^{k}-\delta _{n}^{j}\delta _{m}^{k}\,\!} 。

δ δ -->ijmijk=2δ δ -->mk{\displaystyle \delta _{ijm}^{ijk}=2\delta _{m}^{k}\,\!} 。

δ δ -->ijkijk=6{\displaystyle \delta _{ijk}^{ijk}=6\,\!} 。

δ δ -->lmnijk=ϵ ϵ -->ijkϵ ϵ -->lmn{\displaystyle \delta _{lmn}^{ijk}=\epsilon ^{ijk}\epsilon _{lmn}\,\!} ；

δ δ -->i1i2… … -->inj1j2… … -->jn=ϵ ϵ -->j1j2… … -->jnϵ ϵ -->i1i2… … -->in{\displaystyle \delta _{i_{1}i_{2}\dots i_{n}}^{j_{1}j_{2}\dots j_{n}}=\epsilon ^{j_{1}j_{2}\dots j_{n}}\epsilon _{i_{1}i_{2}\dots i_{n}}\,\!} 。

δ δ -->i1i2… … -->in12… … -->n=ϵ ϵ -->i1i2… … -->in{\displaystyle \delta _{i_{1}i_{2}\dots i_{n}}^{12\dots n}=\epsilon _{i_{1}i_{2}\dots i_{n}}\,\!} 。

δ δ -->i1i2… … -->inj1j2… … -->jnTj1j2… … -->jn=n! Ti1i2… … -->in{\displaystyle \delta _{i_{1}i_{2}\dots i_{n}}^{j_{1}j_{2}\dots j_{n}}T_{j_{1}j_{2}\dots j_{n}}=n!\ T_{i_{1}i_{2}\dots i_{n}}\,\!} ；

其中，Tj1j2… … -->jn{\displaystyle T_{j_{1}j_{2}\dots j_{n}}\,\!} 是 n{\displaystyle n\,\!} 阶张量。

积分表示

对任意的整数 n{\displaystyle n\,\!} ，运用标准的留数计算，可以将克罗内克函数表示成积分的形式：

其中积分的路径是围绕零点逆时针进行。

这个表示方式与下面的另一形式等价：

参见

列维-奇维塔符号

狄拉克测度

同或门

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。