



辛几何
名词由来symplectic这个名词,是赫尔曼·外尔所提出来的。他原来把symplecticgroup(辛群)称为complexgroup,以带出linecomplex的含意。不过complex会令人联想起complexnumber(复数),因此他将complex改为对应的希腊文symplectic一词。complex源自拉丁文complexus一词,词根是co-(共同)+plexus(编织),意为“织在一起”,相对应希腊文词根是sym-plektikos(συμπλεκτικός),结合成symplectic一词。参看辛流形哈密顿力学黎曼几何切触几何参考DusaMcDuffandD.Salamon,IntroductiontoSymplecticTopology,OxfordUniversityPress,1998.ISBN0-19-850451-9.A.T.Fomenko,Symple...
名词由来
symplectic这个名词,是赫尔曼·外尔所提出来的。他原来把symplectic group(辛群)称为complex group,以带出line complex的含意。不过complex会令人联想起complex number(复数),因此他将complex改为对应的希腊文symplectic一词。complex源自拉丁文complexus一词,词根是co-(共同)+plexus(编织),意为“织在一起”,相对应希腊文词根是sym-plektikos(συμπλεκτικός),结合成symplectic一词。
参看
辛流形
哈密顿力学
黎曼几何
切触几何
参考
Dusa McDuff and D. Salamon, Introduction to Symplectic Topology, Oxford University Press, 1998. ISBN 0-19-850451-9.
A. T. Fomenko, Symplectic Geometry (2nd edition) (1995) Gordon and Breach Publishers, ISBN 2-88124-901-9. (Provides an undergrad level introduction.)
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 几何原本

章节大纲欧几里得所著的《几何原本》共分13卷。第一卷至第六卷的内容主要为平面几何。第一卷:几何基础。本卷确立了基本定义、公设和公理,还包括一些关于全等形、平行线和直线形的熟知的定理。第二卷:几何与代数。该卷主要讨论的是毕达哥拉斯学派的几何代数学,主要包括大量代数定理的几何证明。第三卷:圆与角。本卷阐述了圆、弦、割线、切线、圆心角、圆周角的一些定理。第四卷:圆与正多边形。本卷讨论了已知圆的某些内接和外切正多边形的尺规作图问题。第五卷:比例。本卷对欧多克索斯的比例理论进行阐述,第六卷:相似。本卷阐述了比例的属性,以及相似形的概念,包括了泰勒斯定理。第七卷至第九卷主要阐述了数论。第七卷:数论(一)。本卷内容包括整除性、质数、最大公约数、最小公倍数等初等数论内容。第八卷:数论(二)。本卷继续讨论初等数论,包括欧几里得辗转相除法、各种数的关系(如质数、合数、平方数、立方数等)。第九卷:数论(三)。本...
· 双曲几何
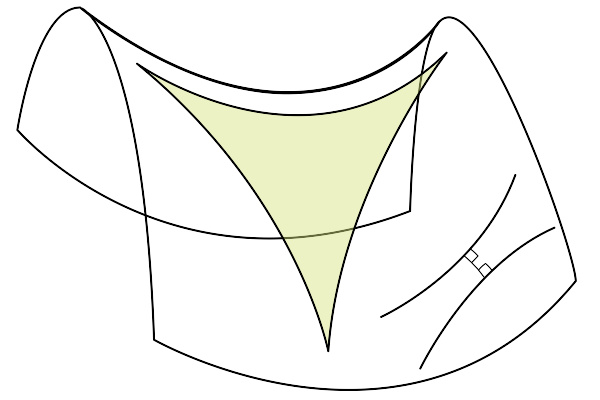
不相交的线已知在双曲几何上,至少有两条直线满足过P点平行直线R。接着在R上取一点B使得PB垂直R于B点,设在所有满足过P点且不与R相交的直线中,存在一条直线x与PB的逆时针方向夹角比其他直线都来的小,即任何一条直线若与PB的逆时针夹角小于x与PB的逆时针夹角,则必与R相交,并定义x为R的渐近线。同理,若存在另一条直线y与PB的顺时针方向夹角比其他直线都来的小,则y为R的另一条渐进线。并且,在所有满足过P点且不与R相交的直线中,唯有x与y是R的渐近线,其余的则称之为R的超平行线。由于满足小于90°且大于x与PB的夹角θ的角度有无线多个,每个角度皆可引出两条R的超平行线,因此R有无线多条超平行线。因此,对于平面上一条直线R以及线外的一点P,恰能引出两条直线过P且渐近于R,以及无限多条直线过P超平行于R。此外,渐进线和超平行线的差别还有:不论往线的哪端延伸,两条超平行线之间的距离皆会趋近于无限;...
· 几何学
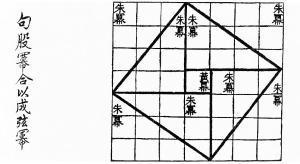
简史几何一词源于《几何原本》的翻译。《几何原本》是世界数学史上影响最为久远,最大的一部数学教科书。《几何原本》传入中国,首先应归功于明末科学家徐光启。徐光启和利玛窦《几何原本》中译本的一个伟大贡献是确定了研究图形的这一学科中文名称为“几何”,并确定了几何学中一些基本术语的译名。“几何”的原文是“geometria”(英文geometry),徐光启和利玛窦在翻译时,取“geo”的音为“几何”(明朝音:gi-ho),而“几何”二字中文原意又有“衡量大小”的意思。用“几何”译“geometria”(英文geometry),音义兼顾,确是神来之笔。几何学中最基本的一些术语,如点、线、直线、平行线、角、三角形和四边形等中文译名,都是这个译本定下来的。这些译名一直流传到今天,且东渡到汉字文化圈的日本、朝鲜等国(越南语则使用独自翻译的越制汉语“形學(hìnhhọc)”一词),影响深远。几何学开始的最早记...
· 计算几何
计算几何算法判断点是否在直线上判断两线段是否相交判断线段和直线是否相交判断点是否在矩形内判断线段、折线、多边形是否在矩形内判断矩形是否在矩形内判断圆是否在矩形内判断矩形是否在圆内判断点是否在多边形内判断线段是否在多边形内判断点是否在圆内判断圆是否在圆内计算点到线段的最近点计算点到圆的最近点及点坐标凸包求法等算法介绍矢量概念如果把一条线段的端点作出次序之分,则可将这种线段看作有向线段。如果有向线段P1P2的起点P1在坐标原点,则把它称为矢量P2。这样,点P(x,y)可以看作起点为原点O(0,0)的二维矢量。相应地,三维空间坐标系下的坐标也可以作类似理解为三维矢量。设二维矢量P=(x1,y1),Q=(x2,y2),则矢量的加法定义为P+Q=(x1+x2,y1+y2),矢量的减法定义为P-Q=(x1-x2,y1-y2)。矢量的加减法有以下性质:P+Q=Q+P,P-Q=-(Q-P)。因为点可视为坐...
· 几何变换
另见爱尔兰根纲领拓扑学刚性变换
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















