拆分数量数列

4可以用5种方法写成和式：4, 3+1, 2+2, 2+1+1, 1+1+1+1。因此 p(4)=5{\displaystyle p(4)=5}。

定义 p(0)=1{\displaystyle p(0)=1}，若n为负数则 p(n)=0{\displaystyle p(n)=0}。

此函数应用于对称多项式及对称群的表示理论等。

分割函数p(n)，n从0开始：

程式实现

#includeusingnamespacestd;intmain(){constintlen=121;intnum[len+1]={1};for(inti=1;i<=len;++i)for(intj=i;j<=len;++j)num[j]+=num[j-i];for(inti=0;i<=len;i++)cout<<i<<" "<<num[i]<<endl;return0;}

Ferrers图示与恒等式

每种分割方法都可用Ferrers图示表示。

Ferrers图示是将第1行放a1{\displaystyle a_{1}}个方格，第2行放a2{\displaystyle a_{2}}个方格……第k{\displaystyle k}行放ak{\displaystyle a_{k}}个方格，来表示整数分割的其中一个方法。

借助Ferrers图示，可以推导出许多恒等式：

给定正整数k和n，n表达成不多于k个正整数之和的方法数目，等于将n分割成任意个不大于k的正整数之和的方法数目。

证明：将表示前者其中一个数组的Ferrers图示沿对角线反射，便得到后者的一个数组。即两者一一对应，因此其数目相同。

例如 k=3，n=6：

此外，

上述恒等式的值亦等于将n+k{\displaystyle n+k}表达成刚好k{\displaystyle k}个正整数之和的方法的数目。

给定正整数n{\displaystyle n}。将n{\displaystyle n}表达成两两相异正整数之和的方法的数目，等于将n{\displaystyle n}表达成奇数之和的方法的数目。

例如n=8{\displaystyle n=8}：

1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

7 + 1

3 + 3 + 1 + 1

5 + 3

5 + 1 + 1 + 1

3 + 1 + 1 + 1 + 1 + 1

8

7 + 1

6 + 2

5 + 3

5 + 2 + 1

4 + 3 + 1

将n{\displaystyle n}表达成p{\displaystyle p}个1和q{\displaystyle q}个2之和，这些方法的数目是第n{\displaystyle n}个斐波那契数。

将n{\displaystyle n}表达成多于1的正整数之和的方法数目是p(n) - p(n-1)。

生成函数

p(n){\displaystyle p(n)}的生成函数是

当|x|<1，右边可写成：

p(n){\displaystyle p(n)}生成函数的倒数为欧拉函数，利用五边形数定理可得到以下的展开式：

将p(n){\displaystyle p(n)}生成函数配合五边形数定理，可以得到以下的递归关系式

其中qi{\displaystyle q_{i}}是第i{\displaystyle i}个广义五边形数。

与杨氏矩阵的关系

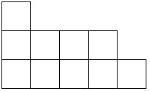
一个 (5, 4, 1)分拆表示的杨表

一个杨氏矩阵与一个整数分拆一一对应，也就是说整数分拆的个数等于相应的杨氏矩阵的个数。如图表示一个10=5+4+1的分拆。利用杨氏矩阵来表示的 分拆更具有直观性，和可处理性，下面是几个例子。

分拆的转置

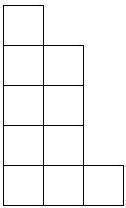
(5, 4, 1)分拆的转置(3, 2, 2,2,1)

整数分拆（10=5+4+1）对应的杨氏矩阵沿x=y轴翻转得到新的杨氏矩阵。它对应分拆为10=3+2+2+2+1。

附加要求的分拆

考虑带有附加条件的分拆。

差分拆

考虑满足下面条件分拆

a1+a2+...+ak=n{\displaystyle a_{1}+a_{2}+...+a_{k}=n} （k{\displaystyle k}的大小不定）

a1>a2...>ak{\displaystyle a_{1}>a_{2}...>a_{k}}

及分拆的每个数都不相等。

生成函数是

奇分拆

考虑满足下面条件分拆

a1+a2+...+ak=n{\displaystyle a_{1}+a_{2}+...+a_{k}=n} （k{\displaystyle k}的大小不定）

a1≥ ≥ -->a2...≥ ≥ -->ak{\displaystyle a_{1}\geq a_{2}...\geq a_{k}}

要求 ai(i=1,2,...,k){\displaystyle a_{i}(i=1,2,...,k)}为奇数

生成函数是

引理

差分拆的个数与奇分拆的个数是一样多的。

可以通过杨表证明。

Rademacher级数

渐近式：

这式子是1918年哈代和拉马努金，以及1920年J. V. Uspensky独立发现的。

1937年，Hans Rademacher得出一个更佳的结果：

其中

(m,n)=1{\displaystyle (m,n)=1}表示m,n{\displaystyle m,n}互质时才计算那项。s(m,k){\displaystyle s(m,k)}表示戴德金和。这条公式的证明用上了福特圆（英语：Ford circle）、法里数列、模群（英语：Modular group）和戴德金η函数。

Elder定理

在将n{\displaystyle n}表示成正整数之和的所有和式之中，任意正整数r{\displaystyle r}作为和项出现在这些式子内的次数，跟每条和式现r{\displaystyle r}次或以上的正整数数目，相同。

当r=1{\displaystyle r=1}时，此定理又称为Stanley定理。

以n=5{\displaystyle n=5}为例：

5

4+1

3+2

3+1+1

2+2+1

2+1+1+1

1+1+1+1+1

1的总出现次数：0+1+0+2+1+3+5=12；在每条和式出现1次或以上的数的数目：1+2+2+2+2+2+1=12

2的总出现次数：0+0+1+0+2+1+0=4；在每条和式出现2次或以上的数的数目：0+0+0+1+1+1+1=4。

pk(n){\displaystyle p_{k}(n)}

当限定将n{\displaystyle n}表示成刚好k{\displaystyle k}个正整数之和时，可以表示为pk(n){\displaystyle p_{k}(n)}。显然，p(n)=∑ ∑ -->k=1npk(n){\displaystyle p(n)=\sum _{k=1}^{n}p_{k}(n)}。

对于n>1{\displaystyle n>1}，pn(n)=p1(n)=1{\displaystyle p_{n}(n)=p_{1}(n)=1}

p2(n)=⌊ ⌊ -->n2⌋ ⌋ -->{\displaystyle p_{2}(n)=\lfloor {\frac {n}{2}}\rfloor } (OEIS:A004526)

p3(n){\displaystyle p_{3}(n)} = 最接近n212{\displaystyle {\frac {n^{2}}{12}}}的正整数。(OEIS:A069905)

pn− − -->1(n)=1{\displaystyle p_{n-1}(n)=1}

pk(n)=pk− − -->1(n− − -->1)+pk(n− − -->k){\displaystyle p_{k}(n)=p_{k-1}(n-1)+p_{k}(n-k)}

其他常见的问题

不少数学家亦有研究按以下方式分拆的方法数目：

将正整数写成模p同余r的正整数之和

将模p同余r正整数写成的正整数之和[1]

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。