二维螺线

费马螺线

等角螺线

双曲螺线

圆内螺线

弯曲螺线

阿基米德螺线

连锁螺线

柯奴螺线

欧拉螺线

阿基米德螺线

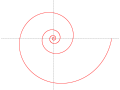
对数螺线

费马螺线

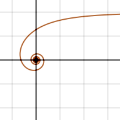
双曲螺线

介绍人名单

Cook, T., 1903. Spirals in nature and art . Nature 68 (1761), 296.

Cook, T., 1979. The curves of life . Dover, New York.

Habib, Z., Sakai, M., 2005. Spiral transition curves and their applications . Scientiae Mathematicae Japonicae 61 (2), 195 – 206.

Dimulyo, S., Habib, Z., Sakai, M., 2009. Fair cubic transition between two circles with one circle inside or tangent to the other . Numerical Algorithms 51, 461–476[1].

Harary, G., Tal, A., 2011. The natural 3D spiral . Computer Graphics Forum 30 (2), 237 – 246[2].

Xu, L., Mould, D., 2009. Magnetic curves: curvature-controlled aesthetic curves using magnetic fields . In: Deussen, O., Hall, P. (Eds.), Computational Aesthetics in Graphics, Visualization, and Imaging. The Eurographics Association[3].

Wang, Y., Zhao, B., Zhang, L., Xu, J., Wang, K., Wang, S., 2004. Designing fair curves using monotone curvature pieces . Computer Aided Geometric Design 21 (5), 515–527[4].

A. Kurnosenko. Applying inversion to construct planar, rational spirals that satisfy two-point G2 Hermite data . Computer Aided Geometric Design, 27(3), 262-280, 2010[5].

A. Kurnosenko. Two-point G2 Hermite interpolation with spirals by inversion of hyperbola . Computer Aided Geometric Design, 27(6), 474-481, 2010.

Miura, K.T., 2006. A general equation of aesthetic curves and its self-affinity . Computer-Aided Design and Applications 3 (1–4), 457–464[6].

Miura, K., Sone, J., Yamashita, A., Kaneko, T., 2005. Derivation of a general formula of aesthetic curves . In: 8th International Conference on Humans and Computers (HC2005). Aizu-Wakamutsu, Japan, pp. 166 – 171[7].

Meek, D., Walton, D., 1989. The use of Cornu spirals in drawing planar curves of controlled curvature . Journal of Computational and Applied Mathematics 25 (1), 69–78[8].

Farin, G., 2006. Class A Bézier curves . Computer Aided Geometric Design 23 (7), 573–581[9].

Farouki, R.T., 1997. Pythagorean-hodograph quintic transition curves of monotone curvature . Computer-Aided Design 29 (9), 601–606.

Yoshida, N., Saito, T., 2006. Interactive aesthetic curve segments . The Visual Computer 22 (9), 896–905[10].

Yoshida, N., Saito, T., 2007. Quasi-aesthetic curves in rational cubic Bézier forms . Computer-Aided Design and Applications 4 (9–10), 477–486[11].

Ziatdinov, R., Yoshida, N., Kim, T., 2012. Analytic parametric equations of log-aesthetic curves in terms of incomplete gamma functions . Computer Aided Geometric Design 29 (2), 129 – 140[12].

Ziatdinov, R., Yoshida, N., Kim, T., 2012. Fitting G2 multispiral transition curve joining two straight lines , Computer-Aided Design 44(6), 591–596[13].

Ziatdinov, R., 2012. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function . Computer Aided Geometric Design 29(7): 510-518[14].

Ziatdinov, R., Miura K.T., 2012. On the Variety of Planar Spirals and Their Applications in Computer Aided Design . European Researcher 27(8-2), 1227-1232[15].

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。