光度
光度学
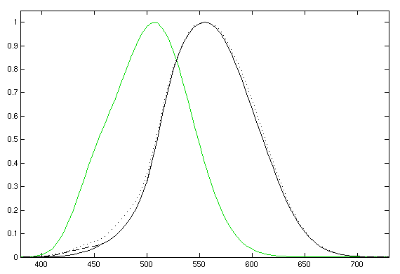
黑色曲线为亮适应光度函数曲线,绿色曲线为暗适应光度函数曲线。实线为CIE 1931标准。断续线为1978年修正数据。点线为2005年修正数据。横坐标单位为nm。
在光度学(photometry)中,"光度"(luminosity)经常与亮度(luminance)弄混。亮度(luminance)是光源在给定方向上单位面积单位立体角内所发出的的光通量,单位是尼特。光度(luminosity)并不是一个物理量,这个词用于光度函数。
光度也指发光强度(Luminous intensity)。
人眼能相当精确地判断两种颜色的光亮暗感觉是否相同。所以为了确定眼睛的光谱响应,可将各种波长的光引起亮暗感觉所需的辐射通量进行比较。在较明亮环境中人的视觉对波长为555.016nm的绿色光最为敏感。设任意波长为λ λ -->{\displaystyle \lambda }的光和波长为555.016nm的光产生同样亮暗感觉所需的辐射通量分别为Ψ Ψ -->555.016{\displaystyle \Psi _{555.016}}和Ψ Ψ -->λ λ -->{\displaystyle \Psi _{\lambda }},把后者和前者之比
叫做光度函数(luminosity function)或视见函数(visual sensitivity function)。例如,实验表明,1mW的555.0nm绿光与2.5W的400.0nm紫光引起的亮暗感觉相同。于是在400.0nm的光度函数值为
衡量光通量的大小,要以光度函数为权重把辐射通量折合成对人眼的有效数量。对波长为λ λ -->{\displaystyle \lambda }的光,辐射强度为ψ ψ -->(λ λ -->){\displaystyle \psi (\lambda )},光通量为Φ Φ -->v{\displaystyle \Phi _{v}},则有
式中Kmax{\displaystyle K_{max}}是波长为555.016nm的光功当量,也叫做最大光功当量,其值为683 lm/W。
天文学
在天文学中,光度(luminosity)是物体每单位时间内辐射出的总能量,即辐射通量,在国际单位制是瓦特(Watt),在厘米克秒制中是“尔格/秒”,天文学常以太阳光度来表示。L⨀ ⨀ -->{\displaystyle L_{\bigodot }};也就是以太阳的辐射通量为一个单位来表示。太阳的光度是3.846×10瓦特。光度以可指辐射通量的谱分布(spectral luminosity),单位为赫兹/赫兹(W/Hz)或瓦特/纳米(W/nm)。
光度是与距离无关的物理量,而人眼观看到的天体的亮度(实际上是照度)则明显的与距离有关,而且是与距离的平方成反比,通常会以视星等来量度。
在测量恒星的亮度时,光度、视星等和距离是相关的参数。如果你已经知道其中的两项,就可以算出第三项。因为太阳的光度是一个标准值,以太阳的视星等和距离做为这些参数的比较标准,就很容易完成彼此之间的转换。
光度和亮度之间的计算
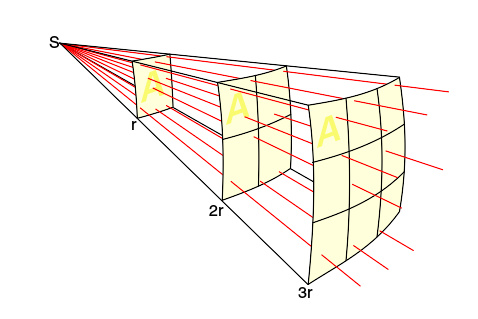
点光源S向所有的方向辐射光线。穿越面积A的总量会随着与光源的距离改变而改变。
假设L{\displaystyle L}是一个点光源的光度(即辐射通量),它向四周辐射的能量是均等的。这个点光源被安置在一个中空球壳的中心,则辐射的所有能量都将穿过这个球壳。当半径增加时,球壳的表面积也将增加,但通过球壳的光度是恒定不变的,所以将导致在球壳上观察到的亮度b{\displaystyle b}下降。
b=LA{\displaystyle b={\frac {L}{A}}},此处A{\displaystyle A}是被照亮的球壳表面积。对恒星和一个点光源而言,A=4π π -->r2{\displaystyle A=4\pi r^{2}}所以b=L4π π -->r2{\displaystyle b={\frac {L}{4\pi r^{2}}}\,},此处r{\displaystyle r}是点光源与观测者的距离。
曾经说明过恒星的光度L{\displaystyle L}(假设恒星是一个黑体,这仅是一个良好的近似值)与温度T{\displaystyle T}和半径R{\displaystyle R}的关联,以方程式表示为:
L=4π π -->R2σ σ -->T4{\displaystyle L=4\pi R^{2}\sigma T^{4}}斯特凡处σ是斯特凡-波兹曼常数5.67×10W·m·K
除以太阳光度L⨀ ⨀ -->{\displaystyle L_{\bigodot }}和消除常数之后,我们得到如下的关系:
LL⨀ ⨀ -->=(RR⨀ ⨀ -->)2(TT⨀ ⨀ -->)4{\displaystyle {\frac {L}{L_{\bigodot }}}={\left({\frac {R}{R_{\bigodot }}}\right)}^{2}{\left({\frac {T}{T_{\bigodot }}}\right)}^{4}}.
对一颗主序星,光度也与质量相关:
LL⨀ ⨀ -->∼ ∼ -->(MM⨀ ⨀ -->)3.9{\displaystyle {\frac {L}{L_{\bigodot }}}\sim {\left({\frac {M}{M_{\bigodot }}}\right)}^{3.9}}
这就很容易知道恒星的光度、温度、半径和质量之间都是有关联的。
恒星的星等与亮间是对数的关系,视星等是从地球上观察到的亮度,绝对星等是在10秒差距上的视星等。 只要知道光度,我们就可以计算在任一给定距离上的视星等:
,此处
mstar是恒星的视星等(一个纯数字)
msun是太阳的视星等(也是一个纯数字)
Lstar是恒星的光度
L⨀ ⨀ -->{\displaystyle L_{\bigodot }}是太阳的光度
rstar是到恒星的距离
rsun是到太阳的距离
很简单的,让msun = −26.73,rsun = 1.58 × 10 光年:
例如:
一颗热星等为−10的明亮恒星的光度是10L⨀ ⨀ -->{\displaystyle L_{\bigodot }},而热星等+17等星的暗星光度是10L⨀ ⨀ -->{\displaystyle L_{\bigodot }}。注意绝对星等可以直接与光度对应,但视星等则是距离的函数。因为只有视星等可以经由观测直接测量,而有了估计的距离才能确定目标的光度。
散射理论和加速器物理
在散射理论和加速器,光度是在单位时间内在标靶的单位面积上所吸收的粒子数目,在cgs单位制下的因次为公分 秒或b s,光度的累积是光度对时间的积分。光度是描述加速器性能和特性的重要数值。
与光度有关的元素
L{\displaystyle L}是光度
N{\displaystyle N}是参与反应的数目。
ρ ρ -->{\displaystyle \rho }是在每一束粒子束内的粒子密度。
σ σ -->{\displaystyle \sigma }是全部的有效截面积。
dΩ Ω -->{\displaystyle d\Omega微分是立体角立体角。
(dσ σ -->dΩ Ω -->){\displaystyle \left({\frac {d\sigma }{d\Omega }}\right)}是微分的有效截面积。
于是有下列的关系存在:
对一个相交的储存环对撞机:
f{\displaystyle f}是交流频率
n{\displaystyle n}是在储存环上的每个良上的线圈数。
Ni{\displaystyle N_{i}}是每一束中的粒子数目。
A{\displaystyle A}是粒子束的截面积。
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读
关于我们

APP下载



























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}