定义

考虑复平面上一个多边形。黎曼映射定理指出存在一个一一对应解析映射f从上半平面

到多边形的内部。函数f把实数轴映射到多边形的边。若多边形内角为α α -->,β β -->,γ γ -->,...{\displaystyle \alpha ,\beta ,\gamma ,...}，那么映射由下式给出：

其中K{\displaystyle K}是常数，a<b<c{\displaystyle \zeta }平面的实轴上的点的值，对应z{\displaystyle z}平面上的多边形施瓦茨。克里斯托费尔称为施瓦茨—克里斯托费尔映射。

为了简便，通常会考虑一种特殊情况，就是当ζ ζ -->{\displaystyle \zeta }无穷远点穷远点映射到z{\displaystyle z}平面的多边形其中一顶点（习惯是内角为α α -->{\displaystyle \alpha }的顶点）。如此，公式的第一个因式实际上是个常数，可以合并进K{\displaystyle K}里。

例子

考虑z{\displaystyle z}平面中的半无穷带。这可以视作顶点是P=0{\displaystyle P=0}, Q=π π -->i{\displaystyle Q=\pi i}和R{\displaystyle R}的三角形，当R{\displaystyle R}趋向无穷大的极限情形。极限时有α α -->=0{\displaystyle \alpha =0}和β β -->=γ γ -->=π π -->/2{\displaystyle \beta =\gamma =\pi /2}。假设我们要找映射f，有f(−1) = Q，f(1) = P，和f(∞) = R，那么f是

计算积分得到

其中C{\displaystyle C}是个（复）积分常数。条件f(− − -->1)=Q{\displaystyle f(-1)=Q}和f(1)=P{\displaystyle f(1)=P}给出C=0{\displaystyle C=0}和K=1{\displaystyle K=1}。因此施瓦茨—克里斯托费尔积分是z=arccoshζ ζ -->{\displaystyle z=\operatorname {arccosh} \,\zeta }。下图描绘这个映射。

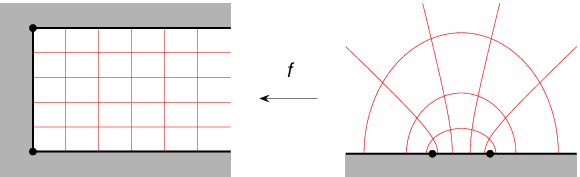
从上半平面到半无穷带的施瓦茨—克里斯托费尔映射

其它简单映射

三角形

到内角为π π -->a{\displaystyle \pi a}，π π -->b{\displaystyle \pi b}和π π -->(1− − -->a− − -->b){\displaystyle \pi (1-a-b)}的三角形的映射是

正方形

从上半平面到正方形的映射是

其中F{\displaystyle F\,}是第一类不完全椭圆积分。

广义三角形

施瓦茨三角形映射把上半平面映射到其边是圆弧的三角形。

参看

在施瓦茨—克里斯托费尔理论现的施瓦茨导数。

参考

Tobin A. Driscoll and Lloyd N. Trefethen, Schwarz-Christoffel Mapping, Cambridge University Press, 2002. ISBN 0-521-80726-3.

Z. Nehari, Conformal Mapping, (1952) McGraw-Hill, New York.

Darren Crowdy，[1]Schwarz-Christoffel mappings to unbounded multiply connected polygonal regions，Math. Proc. Camb. Phil. Soc. (2007)，142, 319.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。