概率空间-族谱新闻-族谱网

概率空间

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:494次

转发:0次

评论:0

定义概率空间(Ω,F,P)是一个总测度为1的测度空间（即P(Ω)=1）.第一项Ω是一个非空集合，有时称作“样本空间”。Ω的集合元素称作“样本输出”，可写作ω。第二项F是样本空间Ω的幂集的一个非空子集。F的集合元素称为事件Σ。事件Σ是样本空间Ω的子集。集合F必须是一个σ-代数：ΦΦ-->∈∈-->F{\displaystyle\Phi{\in}{\mathcal{F}}}；若A∈∈-->F{\displaystyleA{\in}{\mathcal{F}}}，则A¯¯-->∈∈-->F{\displaystyle{\bar{A}}{\in}{\mathcal{F}}}；若An∈∈-->F{\displaystyleA_{n}{\in}{\mathcal{F}}}，n=1,2,...{\displaystylen=1,2,...}，则⋃⋃-->n=1∞∞-->An∈∈-->F{\displays...

定义

概率空间(Ω, F, P)是一个总测度为1的测度空间（即P(Ω)=1）.

第一项Ω是一个非空集合，有时称作“样本空间”。Ω 的集合元素称作“样本输出”，可写作ω。

第二项F是样本空间Ω的幂集的一个非空子集。F的集合元素称为事件Σ。事件Σ是样本空间Ω的子集。集合F必须是一个σ-代数：

Φ Φ -->∈ ∈ -->F{\displaystyle \Phi {\in }{\mathcal {F}}}；

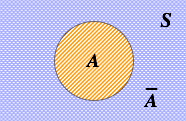
若A∈ ∈ -->F{\displaystyle A{\in }{\mathcal {F}}}，则A¯ ¯ -->∈ ∈ -->F{\displaystyle {\bar {A}}{\in }{\mathcal {F}}}；

若An∈ ∈ -->F{\displaystyle A_{n}{\in }{\mathcal {F}}}，n=1,2,...{\displaystyle n=1,2,...}，则⋃ ⋃ -->n=1∞ ∞ -->An∈ ∈ -->F{\displaystyle \bigcup _{n=1}^{\infty }A_{n}{\in }{\mathcal {F}}}

(Ω, F)合起来称为可测空间。事件就是样本输出的集合，在此集合上可定义其概率。

第三项P称为概率，或者概率测度。这是一个从集合F到实数域R的函数，P:F↦ ↦ -->R{\displaystyle P:\;F{\mapsto }R}。每个事件都被此函数赋予一个0和1之间的概率值。

概率测度经常以黑体表示，例如P{\displaystyle \mathbb {P} }或Q{\displaystyle \mathbb {Q} }，也可用符号"Pr"来表示。

离散模式

离散概率理论仅需要可数集的样本空间Ω Ω -->{\displaystyle \Omega }。概率指的是由概率质量函数p:Ω Ω -->→ → -->[0,1]{\displaystyle p:\Omega \to [0,1]}求得Ω Ω -->{\displaystyle \Omega }上的使得∑ ∑ -->ω ω -->∈ ∈ -->Ω Ω -->p(ω ω -->)=1{\displaystyle \textstyle \sum _{\omega \in \Omega }p(\omega )=1}的点。Ω Ω -->{\displaystyle \Omega } 全部的子集合可视为随机事件（也就是F=2Ω Ω -->{\displaystyle {\mathcal {F}}=2^{\Omega }}为幂集）。概率测度可简写为

(∗ ∗ -->)P(A)=∑ ∑ -->ω ω -->∈ ∈ -->Ap(ω ω -->)for all A⊆ ⊆ -->Ω Ω -->{\displaystyle (*)\qquad P(A)=\sum _{\omega \in A}p(\omega )\quad {\text{for all }}A\subseteq \Omega }

使用σ-代数F=2Ω Ω -->{\displaystyle {\mathcal {F}}=2^{\Omega }}能够完整描述样本空间。一般来说，σ-代数相当于一个有限或集合划分合划分Ω Ω -->=B1∪ ∪ -->B2∪ ∪ -->… … -->{\displaystyle \Omega =B_{1}\cup B_{2}\cup \dots }，事件A的一般型A∈ ∈ -->F{\displaystyle A\in {\mathcal {F}}} 且A=Bk1∪ ∪ -->Bk2∪ ∪ -->… … -->{\displaystyle A=B_{k_{1}}\cup B_{k_{2}}\cup \dots }

p(ω ω -->)=0{\displaystyle p(\omega )=0}是被定义允许的情况但极少使用，因为如此的ω ω -->{\displaystyle \omega }可以安全的从样本空间中移除。

一般模式

如果Ω不可数，存在某些ω使得p(ω) ≠ 0 的情况仍然存在，那些ω称为原子。他们大部分都是可数的集合（有可能为空集合），其可能性为所有原子概率的和。如果这个和等于1，那么其他的点可以安全地从样本空间中移除，回归离散模式。反之，如果和少与1（有可能为零）那么概率空间分解成为离散（原子）部分（可能为零），以及非原子部分。

例子

若样本空间是关于一个机会均等的抛硬币动作，则样本输出为“正面”或“反面”。事件为：

{正面}，其概率为0.5。

{反面}，其概率为0.5。

{ }=∅ 非正非反，其概率为0.

{正面，反面}，不是正面就是反面，这是Ω，其概率为1。