描述

给定曲面上的磁通量大小与通过曲面的磁场线的个数成正比。此处磁场线的个数是个“净”数量，即从一个方向上通过的个数减去另一个方向上通过的个数。当一个均匀磁场垂直通过一个平面，磁通量即是磁场与该平面面积的乘积。当均匀磁场 B {\displaystyle \mathbf {B} } 以任意角度通过一个平面，磁通量即是磁场与该平面面积 a {\displaystyle \mathbf {a} } 的点积。

其中， θ θ --> {\displaystyle \theta } 是磁场 B {\displaystyle \mathbf {B} } 和平面面积法矢量 a {\displaystyle \mathbf {a} } 的夹角.

图1：曲面积分的定义基于将曲面分割成小的曲面元。每个曲面元对应一个矢量 d S {\displaystyle d\mathbf {S} } 。该矢量的大小即曲面元的面积，方向为指向外部的法矢量。

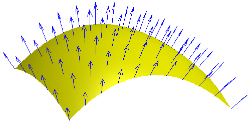
图2：曲面法矢量的矢量场。

在一般情况下，磁通量是通过磁场在曲面面积上的积分定义的（见图1和图2）。

其中， Φ Φ --> B {\displaystyle \Phi _{B}\ } 为磁通量， B {\displaystyle \mathbf {B} } 为磁感应强度， S {\displaystyle S} 为曲面， ⋅ ⋅ --> {\displaystyle \cdot } 为点积， d S {\displaystyle d\mathbf {S} } 为无曲面积分（见曲面积分）。

磁通量通常通过通量计进行测量。通量计包括测量线圈以及估计测量线圈上电压变化的电路，从而计算磁通量。

通过闭曲面的磁通量

高斯磁定律是四条麦克斯韦方程之一，指出通过一闭曲面的磁通量为零。这定律是依据还没有发现磁单极这一经验得出的。

高斯磁定律为，对任意闭曲面：

通过开曲面的磁通量

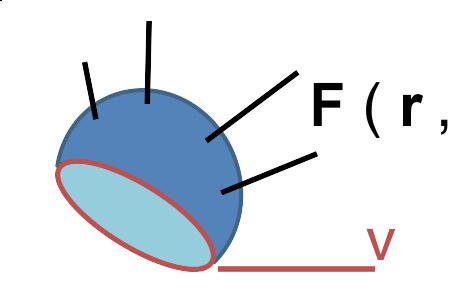
图3：空间中的矢量场 F ( r , t )以及曲面Σ。∂Σ为曲面Σ的边界，以速度 v 运动。考虑矢量场在曲线∂Σ上的积分。

即使通过闭曲面的磁通量是零，通过开曲面的磁通量可以不是零，而且，它是电磁学中一个重要的物理量。例如，当通过一个导电线环的磁通量发生变化，这一变化会引起电动势的生成，并因此在线环中产生电流。其关系式可由法拉第电磁感应定律得出：

其中（见图3）：

在上述公式中，电动势的生成可以有两种解释：由洛伦兹力引起的电荷在闭合曲线 ∂ ∂ --> Σ Σ --> ( t ) {\displaystyle \partial \Sigma (t)} 上的运动；通过开曲面 Σ Σ --> ( t ) {\displaystyle \Sigma (t)} 的磁通量。这一公式即是发电机的原理。

与电通量的比较

麦克斯韦方程中的高斯电场定律为：

其中

注意，通过闭曲面的E {\displaystyle \mathbf {E} } 的通量“并不总是”零，这指出了电“单极”的存在，即自由的正负电荷。

参见

磁场：代表磁力线的密度。

麦克斯韦方程组：是一组四条偏微分方程，被詹姆斯·麦克斯韦用作描述电场和磁场，以及它们与物质之间的相互作用。

高斯定律：给出从一密闭表面流出的电通量及表面圈住的电荷之间的关系式。

磁单极：是一种大概能不严谨地被形容为“只有单极的磁铁”的理论粒子。

磁通量量子：是流经超导体的磁通量的量子。

卡尔·高斯：跟物理教授威廉·韦伯的合作发展出成果丰硕的研究；它使得磁学领域得到了新知识。

詹姆斯·麦克斯韦：证明了电力和磁力是电磁的两个互补层面。

法拉第吊诡：关于法拉第电磁感应定律的吊诡。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。