导言

定义

简单来说，所谓的一个 集合 ，就是将数个对象归类而分成为一个或数个形态各异的大小整体。 一般来讲，集合是具有某种特性的事物的整体，或是一些确认对象的汇集。构成集合的事物或对象称作 元素 或是 成员 。集合的元素可以是任何事物，可以是人，可以是物，也可以是字母或数字等。

在数学交流当中为了方便，集合会有一些别名。比如：

族、系　通常指它的元素也是一些集合。

符号

元素通常用 a , b , c , d , x {\displaystyle a,\ b,\ c,\ d,\ x} 等小写字母来表示；而集合通常用 A , B , C , D , X {\displaystyle \mathbf {A,\ B,\ C,\ D,\ X} } 等字母来表示。

当元素 a {\displaystyle a} 属于集合 A {\displaystyle \mathbf {A} } 时，记作 a ∈ ∈ --> A {\displaystyle a\in \mathbf {A} } 。

当元素 a {\displaystyle a} 不属于集合 A {\displaystyle \mathbf {A} } 时，记作 a ∉ A {\displaystyle a\not \in \mathbf {A} } 。

如果 A , B {\displaystyle \mathbf {A,\ B} } 两个集合所包含的元素完全一样，则二者相等，写作 A = B {\displaystyle \mathbf {A=B} } 。

集合的特性

无序性 ：一个集合中，每个元素的地位都是相同的，元素之间是无序的。

集合上可以定义序关系，定义了序关系后，元素之间就可以按照序关系排序。但就集合本身的特性而言，元素之间没有必然的序。（参见序理论）

互异性 ：一个集合中，任何两个元素都认为是不相同的，即每个元素只能出现一次。

有时需要对同一元素出现多次的情形进行刻画，可以使用多重集，其中的元素允许出现多次。

确定性 ：给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现。

集合的表示

集合可以用文字或数学符号描述，称为 描述法 ，比如：

集合的另一种表示方法是在大括号中列出其元素，称为 列举法 ，比如：

尽管两个集合有不同的表示，它们仍可能是相同的。比如：上述集合中， A = C 而 B = D ，因为它们正好有相同的元素。

元素列出的顺序不同，或者元素列表中有重复，都没有关系。比如：这三个集合 {2, 4}，{4, 2} 和 {2, 2, 4, 2} 是相同的，同样因为它们有相同的元素。

集合在不严格的意义下也可以通过草图来表示，更多信息，请见文氏图。

集合间的关系

子集与包含关系

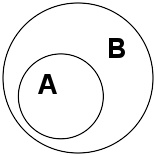
B的子集A

定义

集合A，B，若∀a∈A，有a∈B∴A⊆B。则称A是B的 子集 ，亦称A 包含于 B，或B 包含 A，记作A⊆B。

若A⊆B，且A≠B，则称A是B的 真子集 ，亦称A 真包含于 B，或B 真包含 A，记作A⊂B。

基本性质

包含关系“⊆”是集合间的一个 非严格偏序关系 ，因为它有如下性质：

真包含关系“⊂”是集合间的一个 严格偏序关系 ，因为它有如下性质：

显然，包含关系，真包含关系定义了集合间的偏序关系。而Ø是这个偏序关系的 最小元素 ，即：∀集合S，Ø⊆S；且若S≠Ø，则Ø⊂S，（空集是任何集合的子集，是任何非空集合的真子集）

举例

集合的运算

并

两个集合可以相"加"。A和B的 并集 是将A和B的元素放到一起构成的新集合。

定义

给定集合A，B，定义运算∪如下：A∪B = {e|e∈A 或 e∈B}。A∪B称为A和B的 并集 。

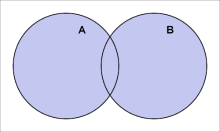
A 和 B 的并集

示例

基本性质

作为集合间的二元运算，∪运算具有以下性质。

交换律 ：A∪B = B∪A；

结合律 ：(A∪B)∪C = A∪(B∪C)；

幂等律 ：A∪A = A；

幺元 ：∀集合A，A∪ ∅ ∅ --> {\displaystyle \varnothing } = A；（ ∅ ∅ --> {\displaystyle \varnothing } 是∪运算的幺元）。

交

一个新的集合也可以通过两个集合"共"有的元素来构造。 A 和 B 的 交集 ，写作 A ∩ B ，是既属于 A 的、又属于 B 的所有元素组成的集合。

若 A ∩ B = ∅ ∅ --> {\displaystyle \varnothing } ，则 A 和 B 称作 不相交 。

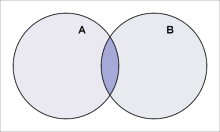
A 和 B 的交集

定义

给定集合A，B，定义运算∩如下：A∩B = {e|e∈A 且 e∈B}。A∩B称为A和B的 交集 。

基本性质

作为集合间的二元运算，∩运算具有以下性质。

交换律 ：A∩B = B∩A；

结合律 ：(A∩B)∩C = A∩(B∩C)；

幂等律 ：A∩A = A；

空集合 ：∀集合A，A∩ ∅ ∅ --> {\displaystyle \varnothing } = ∅ ∅ --> {\displaystyle \varnothing } ；（ ∅ ∅ --> {\displaystyle \varnothing } 是∩运算的空集合）。

其它性质还有：

A⊆B ⇒ A∩B = A

示例

差

两个集合也可以相"减"。 A 在 B 中的 相对补集 ，写作 B − A ，是属于 B 的、但不属于 A 的所有元素组成的集合。

在特定情况下，所讨论的所有集合是一个给定的全集 U 的子集。这样， U − A 称作 A 的 绝对补集 ，或简称 补集 （余集），写作 A ′或 C U A 。

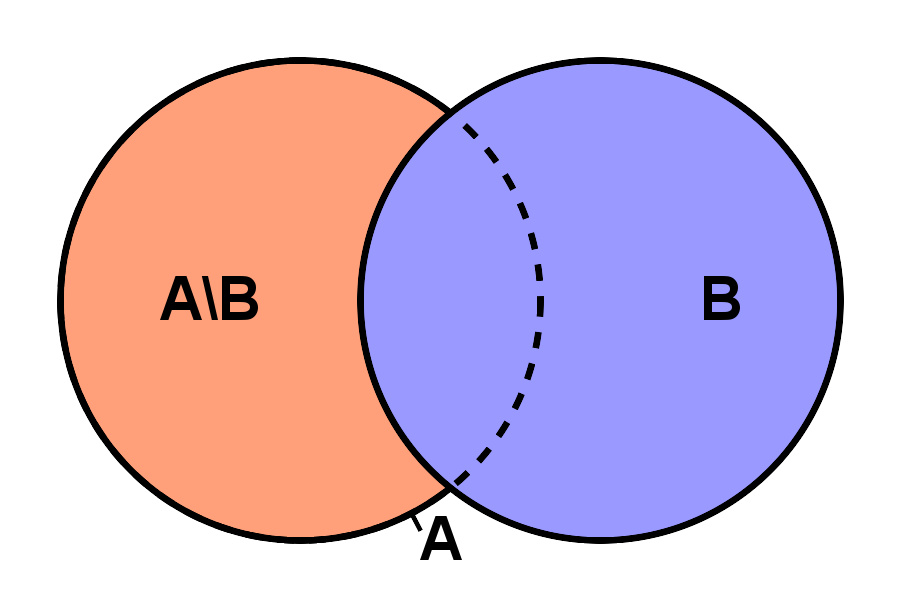
相对补集 A - B

补集可以看作两个集合相减，有时也称作 差集 。

定义

给定集合A，B，定义运算-如下：A - B = {e|e∈A 且 e ∉ ∉ --> {\displaystyle \notin } B}。A - B称为B对于A的 差集 ， 相对补集 或 相对余集 。

在上下文确定了 全集 U时，对于U的某个子集A，一般称U - A为A（对于U）的 补集 或 余集 ，通常记为A"或 A ¯ ¯ --> {\displaystyle {\bar {A}}} ，也有记为C U A的。

基本性质

作为集合间的二元运算，- 运算有如下基本性质：

A - A = ∅ ∅ --> {\displaystyle \varnothing } ；

右幺元 ：∀集合A，A - ∅ ∅ --> {\displaystyle \varnothing } = A；（ ∅ ∅ --> {\displaystyle \varnothing } 是 - 运算的右幺元）。

左零元 ：∀集合A， ∅ ∅ --> {\displaystyle \varnothing } - A = ∅ ∅ --> {\displaystyle \varnothing } ；（ ∅ ∅ --> {\displaystyle \varnothing } 是 - 运算的左零元）。

示例

对称差

定义

给定集合A，B，定义 对称差 运算△如下：A△B = (A-B)∪(B-A)。

基本性质

作为集合间的二元运算，△运算具有如下基本性质：

交换律 ：A△B = B△A；

结合律 ：(A△B)△C = A△(B△C)；

幺元 ：∀集合A，A△ ∅ ∅ --> {\displaystyle \varnothing } = A；（ ∅ ∅ --> {\displaystyle \varnothing } 是△运算的幺元）。

逆元 ：A△A = ∅ ∅ --> {\displaystyle \varnothing } ；

集合的元素个数

上述每一个集合都有确定的元素个数；比如：集合 A 有三个元素、而集合 B 有四个。一个集合中元素的数目称为该集合的基数。数学写法有很多种，不同作者及不同书本用不同的写法: Card ⁡ ⁡ --> ( A ) , # # --> A , | A | , A ¯ ¯ --> , A ¯ ¯ --> ¯ ¯ --> {\displaystyle \operatorname {Card} (A),\ \#A,\ |A|,\ {\bar {A}},\ {\bar {\bar {A}}}} 。

集合可以没有元素。这样的集合叫做 空集 ，用 { } {\displaystyle \{\}} 或符号 ∅ ∅ --> {\displaystyle \varnothing } 表示。比如：在2004年，集合 A 是所有住在月球上的人，它没有元素，则 A = ∅ ∅ --> {\displaystyle \varnothing } 。在数学上，空集非常重要。空集信息请看空集。

如果集合只含有限个元素，那么这个集合可以称为 有限集合 。

集合也可以有无穷多个元素，这样的集合称为 无限集合 。比如：自然数集便是无限集合。关于无穷大和集合的大小的更多信息请见集合的势。

公理化集合论

若把集合看作“符合任意特定性质的一堆东西”，会得出所谓罗素悖论。为解决罗素悖论，数学家提出公理化集合论。在公理集合论中，集合是一个不加定义的概念。

类

在更深层的公理化数学中， 集合 仅仅是一种特殊的类，是“良性类”，是能够成为其它类的元素的类。

类区分为两种：一种是可以顺利进行类运算的“ 良性类 ”，我们把这种“良性类”称为 集合 ；另一种是要限制运算的“ 本性类 ”，对于本性类，类运算并不是都能进行的。

定义 类A如果满足条件“ ∃ ∃ --> B ( A ∈ ∈ --> B ) {\displaystyle \exists B(A\in B)} ”，则称类A为一个 集合 (简称为 集 )，记为 Set ⁡ ⁡ --> ( A ) {\displaystyle \operatorname {Set} (A)} 。否则称为 本性类 。

这说明，一个集合可以作为其它类的元素，但一个本性类却不能成为其它类的元素。因此可以理解为“本性类是最高层次的类”。

参考文献

Dauben, Joseph W., Georg Cantor: His Mathematics and Philosophy of the Infinite , Boston: Harvard University Press (1979) ISBN 978-0-691-02447-9.

Halmos, Paul R., Naive Set Theory , Princeton, N.J.: Van Nostrand (1960) ISBN 0-387-90092-6.

Stoll, Robert R., Set Theory and Logic , Mineola, N.Y.: Dover Publications （ 英语 ： Dover Publications ） (1979) ISBN 0-486-63829-4.

参见

公理化数学

类的理论

罗素公理体系

集合代数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。