r的值对结果的影响

变化参数 r {\displaystyle r} 的值，其结果如下：

0和1之间：不论启始值数值为何， x n {\displaystyle x_{n}} 会越来越少，最后趋近于0。

1和2之间：不论启始值数值为何， x n {\displaystyle x_{n}} 会快速的趋近 r − − --> 1 r {\displaystyle {\frac {r-1}{r}}} 。

2和3之间：经过几次迭代， x n {\displaystyle x_{n}} 也会越来越接近 r − − --> 1 r {\displaystyle {\frac {r-1}{r}}} ，但一开始会在这个值左右振动，而收敛速率是线性的。

3： x n {\displaystyle x_{n}} 仍然会越来越接近 r − − --> 1 r {\displaystyle {\frac {r-1}{r}}} ，但收敛速率极为缓慢，不是线性的。

3和 1 + 6 {\displaystyle 1+{\sqrt {6}}} （约3.45）之间：针对几乎所有的初值， x n {\displaystyle x_{n}} 最后会在2个值之间持续的震荡，即 x n {\displaystyle x_{n}} 最后会是a,b,a,b...的变化，其数值和 r {\displaystyle r} 有关。

3.45和大约3.54之间，针对几乎所有的初值， x n {\displaystyle x_{n}} 最后会在4个值之间持续的震荡。

约大于3.54： x n {\displaystyle x_{n}} 最后会在8个、16个、32个值……之间持续的震荡，至于 r {\displaystyle r} 何时会令 x n {\displaystyle x_{n}} 的值由n个到2n个，则和费根鲍姆常数 δ δ --> = 4.669... {\displaystyle \delta =4.669...} 有关。

约为3.5699：这样的振动消失，整个系统开始在混沌的状态之中。针对几乎所有的初值，都不会出现固定周期的震荡，初值再微小的变化，随着时间都会使结果产生明显的差异，这就是典型混沌的特性。

大于3.5699：整个系统在混沌的状态之中。不过，当中有些特定的 r {\displaystyle r} 值还是使系统变成非混沌，有周期性的结果，这些区间称为“稳定岛”。例如当 r {\displaystyle r} 约大于3.82，会出现3个值的周期，再大一点出现6个值及12个值的周期。

当 r {\displaystyle r} 从大约3.5699到大约3.8284之间，系统混沌性质发展的现象有时会称为 Pomeau–Manneville场景 （ 英语 ： Pomeau–Manneville scenario ） ，其特征是周期性的震荡和非周期性的行为会穿插出现。此特征可以应用在半导体元件中 。也有其他区域会使系统的周期为5个值，不管任意周期都存在某特定的 r {\displaystyle r} ，使周期为指定值。

大于4：针对几乎所有的初值，系统最后都会超过区间[0,1]并且发散。

对于任一个 r {\displaystyle r} 值，最多只有一个稳定的极限环，若稳定极限环存在，几乎所有的点最后都会趋近极限 。若某一个 r {\displaystyle r} 值有一个稳定的极限环，可能也有无限个不同周期的不稳定极限。

这些情况可用 分枝图 （ 英语 ： Bifurcation diagram ） 表示，分枝图中的横轴是参数 r {\displaystyle r} 的数值，纵轴中显示大部分初值下，稳态可能的 x {\displaystyle x} 值，若最后数值会在2个值中震荡，分枝图上对应的数值就会有2点。若某特定 r {\displaystyle r} 值下，已无法明确的看到有几个对应的点，当时系统可能已经在混沌状态下。

分枝图有自相似的特性。若将分枝图中 r = 3.82 {\displaystyle r=3.82} 的部分展开，只取三个分支中的一个。其图形会好像是原分枝图缩放及扭曲后的结果。针对所有非混沌的参数 r {\displaystyle r} 都有此一特性。以此可以看出混沌和分形深入及明显的关系。

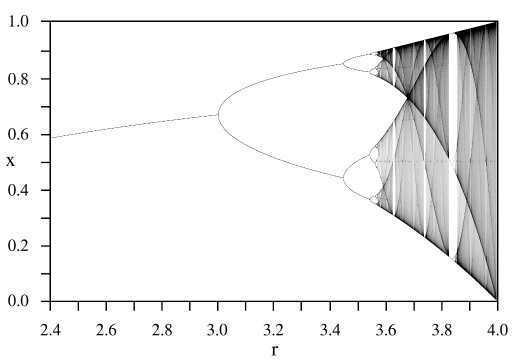
单峰映象和混沌

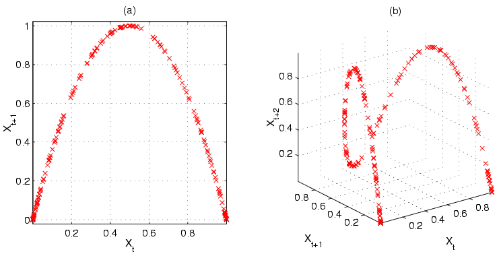
r=4的单峰映象，二维及三维的相图，其中可看出其拉伸及折叠的特性

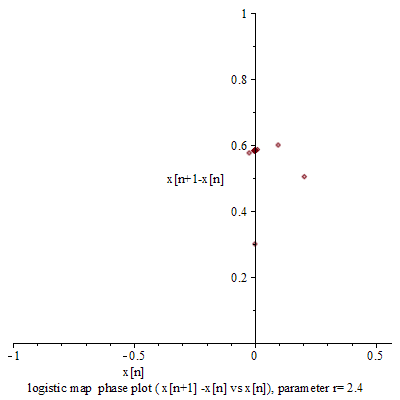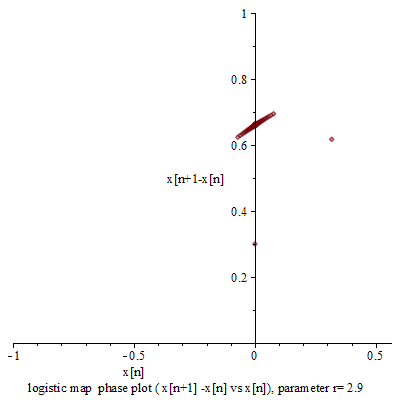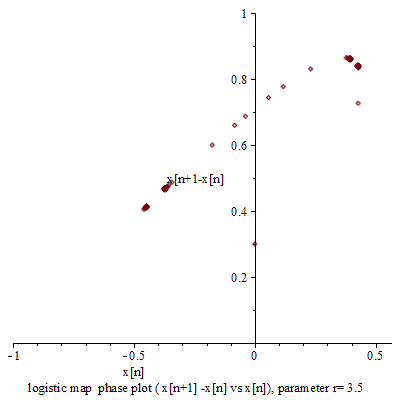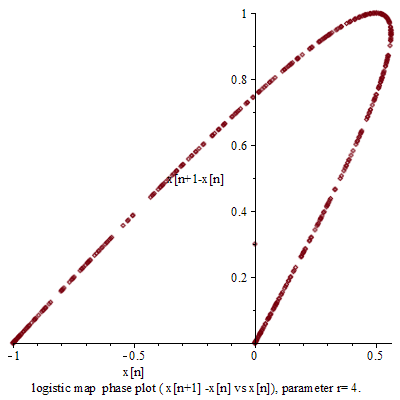
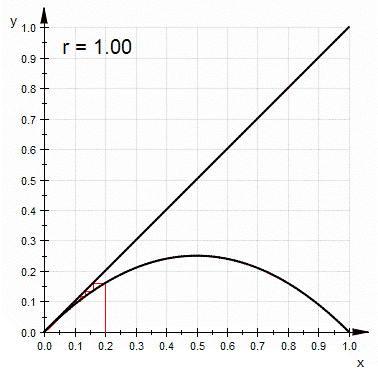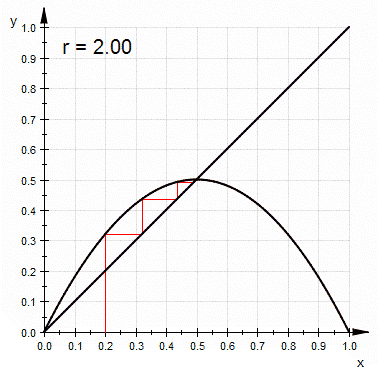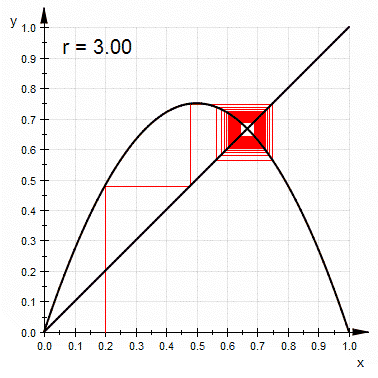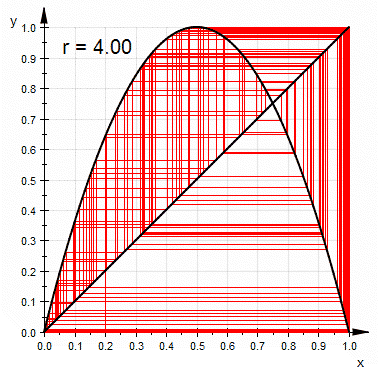
单峰映象的 蛛网图 （ 英语 ： cobweb diagram ） ，在超过3.57的大部分r值可看出其混沌的特性

和其他混沌系统比较，单峰映象较为简单，是一个说明混沌特性的很好的例子。简单来说，混沌就是对初始条件的高度灵敏度。 r {\displaystyle r} 是在3.57及4之间的大部分数值都可以使单峰映象出现此一特性。对初始条件有高度灵敏度的常见原因是映射本身是对定义域的拉伸及折叠。单峰映象的二次差分方程可视为是对于区间(0,1)拉伸及折叠的过程。

利用二维及三维的相图可以看出一些单峰映象的特性。以 r = 4 {\displaystyle r=4} 的单峰映象为例，二维相图为一抛物线，但是若用 ( x n , x n + 1 , x n + 2 ) {\displaystyle (x_{n},x_{n+1},x_{n+2})} 绘制三维相图，可看出进一步的结构，例如几个一开始很接近的点在迭代后开始发散．特别是位在斜率较大位置的点。

拉伸及折叠的结果使迭代的数列以指数形式发散（参照李亚普诺夫指数），可以用有混沌特性时，单峰映象的复杂及不可预测性说明这一点。事实上，数列的指数发散说明了混沌和不可预测性之间的关系：初值微小的误差在迭代过程中会以指数成长的方式增加。因此当对于初始状态的资讯中有微小的误差时．对未来状态的预测准确度也会随迭代次数增加而快速变差。

由于映象是限制在实数数线的一段范围内，其维度小于或等于1。依数值分析的结果，在r=3.5699456...时（刚开始混沌特性时），其 关联维度 （ 英语 ： correlation dimension ） 为0.500 ± 0.005 （Peter Grassberger,1983）、豪斯多夫维数大约是0.538 ，而分形维数为0.5170976... 。

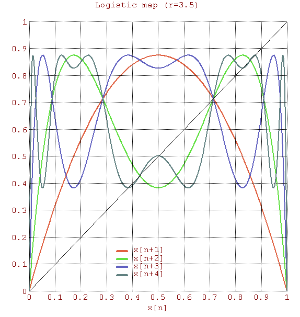
r=3.5的单峰映象，在头三次迭代后的函数

有些混沌系统可对于其未来状态的可能性作准确的描述。若一个可能有混沌特性的动态系统存在吸引子，则存在一 概率量测 （ 英语 ： Probability measure ） 描述系统长期下，在吸引子各部分所花时间的比例。以 r = 4 {\displaystyle r=4} 的单峰映象而言，启始状态在区间(0,1)中，而吸引子也在间(0,1)中，其概率量测对应参数 a = 0.5 , b = 0.5 {\displaystyle a=0.5,b=0.5} 的Β分布 ，其 不变测度 （ 英语 ： invariant measure ） 为 π π --> − − --> 1 x − − --> 1 / 2 ( 1 − − --> x ) − − --> 1 / 2 {\displaystyle \pi ^{-1}x^{-1/2}(1-x)^{-1/2}} 。不可预期性和随机不同，不过在一些情形下这二很类似，而且即使我们对单峰映象（或其他混沌系统）初值只有很少的资讯，仍然可以针对长期的分布作某种程度的预测。

部分情形下的解

在 r = 4 {\displaystyle r=4} 及 r = 2 {\displaystyle r=2} 的特殊情形下，单峰映象有解析解 。不过大部分情形下的通解只能以统计的方式预测 。 r = 4 {\displaystyle r=4} 的解为

其中初始条件参数 θ θ --> {\displaystyle \theta } 是由 θ θ --> = 1 π π --> sin − − --> 1 ⁡ ⁡ --> ( x 0 1 / 2 ) {\displaystyle \theta ={\tfrac {1}{\pi }}\sin ^{-1}(x_{0}^{1/2})} 求得。针对有理数的 θ θ --> {\displaystyle \theta } ，有限次数的迭代后 x n {\displaystyle x_{n}} 就会变成一个周期性的数列。不过几乎所有的 θ θ --> {\displaystyle \theta } 都是无理数，此时 x n {\displaystyle x_{n}} 不会重复，因此没有周期解。此解可以清楚的看出混沌的二个重要特征：拉伸及折叠。系数2 表示拉伸的指数成长，因此造成蝴蝶效应，也就是对初始值的高度灵敏性，而解中包括正弦函数的平方，使解折叠在[0, 1]的范围内。

r = 2 {\displaystyle r=2} 的解为：

x n = 1 2 − − --> 1 2 ( 1 − − --> 2 x 0 ) 2 n {\displaystyle x_{n}={\frac {1}{2}}-{\frac {1}{2}}(1-2x_{0})^{2^{n}}}

对于 x 0 ∈ ∈ --> [ 0 , 1 ) {\displaystyle x_{0}\in [0,1)} 。此解没有混沌的特性。由于对于不包括不稳定固定点0在内的 x 0 {\displaystyle x_{0}} ，当 n 趋近无限大时 ( 1 − − --> 2 x 0 ) 2 n {\displaystyle (1-2x_{0})^{2^{n}}} 会趋近于零，因此 x n {\displaystyle x_{n}} 会趋近稳定的固定点 1 2 . {\displaystyle {\tfrac {1}{2}}.} 。

r = 4时找任意周期的循环

r = 4时，几乎所有的初值都会使单峰映象出现混沌特性，不过也存在无限个初值会使单峰映象最后呈周期性变化，而且对于所有正整数，都存在一初值使单峰映象的周期为该正整数。可以利用单峰映象和 位元位移映射 （ 英语 ： bit-shift map ） 之间的关系来找出任何周期的循环。若 x 依照单峰映象 x n + 1 = 4 x n ( 1 − − --> x n ) {\displaystyle x_{n+1}=4x_{n}(1-x_{n})\,} 而 y 依照位元位移映射

则二个变数的关系如下：

位元位移映射其名称是因为当 y 以二进制表示时，映射会将二进制的数字左移一位。例如若数字是二进制的循环小数，循环节为001，则位元位移映射的序列为001001001... →010010010... →100100100... →001001001...，为周期为3的循环，循环节为010, 011, 100, 101, 110 时也会有类似情形，这些循环小数都可以转换为对应的分数，上例若以分数表示为：1/7 → 2/7 → 4/7 → 1/7。转换到r=4的单峰映象后，为611260467... → .950484434... → .188255099... → .611260467...。其他周期为3的循环也可以转换为单峰映象。依相同方式也可以找出在 位元位移映射下，任意周期的循环，再转换为单峰映象。

不过几乎所有在区间[0, 1)的数字都是无理数，而初始值为无理数的位元位移映射没有循环的特性，因此对应的单峰映象也没有循环的特性。

相关条目

混沌理论

刚性方程

李雅普诺夫稳定性

参考资料

教科书

Sprott, Julien Clinton. Chaos and Time-Series Analysis. Oxford University Press. 2003. ISBN 0-19-850840-9.

Strogatz, Steven. Nonlinear Dynamics and Chaos. Perseus Publishing. 2000. ISBN 0-7382-0453-6.

Tufillaro, Nicholas; Tyler Abbott, Jeremiah Reilly. An experimental approach to nonlinear dynamics and chaos. Addison-Wesley New York. 1992. ISBN 0-201-55441-0.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。