定义

正弦波波长λ可以通过测量相位相同的任意相邻两点间的距离得到，这两点可以是相邻的波峰、波谷或是如图所示的零交点（英语：Zero crossing）。

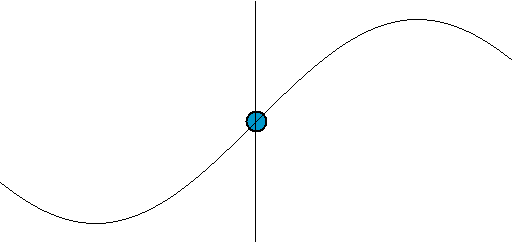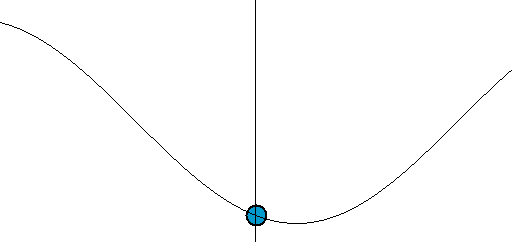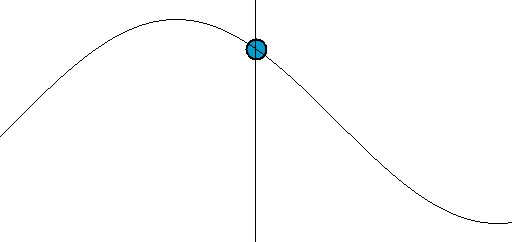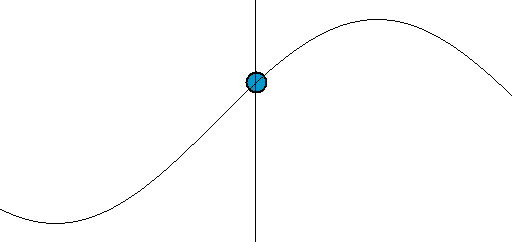
当波行进时，给定点的值以正弦作正弦振动。

波矢有两种常见的定义，区别在于振幅因子是否乘以2π π -->{\displaystyle 2\pi }，两种定义分物理学物理学和晶体学以及它们的相关领域。

物理学定义

理想的一维行波遵循如下方程：

其中：

x为位置；

t为时间；

ψ ψ -->{\displaystyle \psi }（x和t的函数）是对波进行描述的扰动（例海浪于海浪，ψ ψ -->{\displaystyle \psi }是超出水面声波度；对于声波，ψ ψ -->{\displaystyle气压psi }是超气压）；

A是波的振幅（振动的峰值）；

φ φ -->{\displaystyle \varphi }是相位偏移，描述了两个波互相之间不同步的程度；

ω ω -->{\displaystyle \omega }是波的角频率，描述了在一个给定点波振动的快慢程度；

k{\displaystyle k}是波数，与波长成反比，由k=2π π -->/λ λ -->{\displaystyle k=2\pi /\lambda }求出。

此波在+x方向上行进，相速度为ω ω -->/k{\displaystyle \omega /k}。

推广到三维情况下，方程为：

其中：

r是三维空间中的位置矢量；

⋅ ⋅ -->{\displaystyle \cdot } 是矢量点积；

k是波矢。

这一方程描述了平面波。一维情况下，波矢的大小是角波数|k|=2π π -->/λ λ -->{\displaystyle |{\mathbf {k} }|=2\pi /\lambda }。波矢的方向是平面波行进的方向。

晶体学定义

在晶体学中，描述相同的波的方程略有不同。在一维和三维情况下的方程分别为：

不同点在于：

晶体学定义使用了频率ν ν -->{\displaystyle \nu }，而不是角频率ω ω -->{\displaystyle \omega }，由公式2π π -->ν ν -->=ω ω -->{\displaystyle 2\pi \nu =\omega }，二者可以相互转换。这种置换主要反映了在晶体学中的常见应用。

波数k以及波矢k的定义方式不同。此处的k=|k|=1/λ λ -->{\displaystyle k=|{\mathbf {k} }|=1/\lambda }，而在物理学定义中，k=|k|=2π π -->/λ λ -->{\displaystyle k=|{\mathbf {k} }|=2\pi /\lambda }。

狭义相对论

接近单色光的波包可以由波矢

准确描述，若明确的改写成共变和反变形式，则

于是波矢的大小为

最后一步等于零是因为对于真空中的光满足

洛伦兹变换

对波矢作洛伦兹变换可导出相对论性多普勒效应。洛伦兹矩阵定义为

在光被快速移动的波源激发的情况下，若要在地球坐标系（实验室坐标系）中检定光的频率，就要使用洛伦兹变换，如下所示。注意波源位于坐标系S，地球位于观测系S。 对波矢进行洛伦兹变换得到

只考虑μ μ -->=0{\displaystyle \mu =0}分量的情况，得到

因此

波源远离观测者

当波源径直地远离观测者时，θ θ -->=π π -->{\displaystyle \theta =\pi }，方程变为：

波源接近观测者

当波源径直地接近观测者时，θ θ -->=0{\displaystyle \theta =0}，方程变为：

参考文献

Brau, Charles A. Modern Problems in Classical Electrodynamics. Oxford University Press. 2004. ISBN 0-19-514665-4. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。