轨道

明确的说，倾角是描述天体轨道的形状和方向的六个轨道要素之一。它是行星的轨道平面和参考平面（通常以黄道或赤道为主）之间的角距离，并以角度来描述。

在太阳系，行星轨道的倾角（在图一中标示为 i ）被定义为行星的轨道平面和黄道— －地球绕太阳轨道所位于的平面 － 的角距离。它也可能以另一个平面来测量，例如太阳的赤道或木星的轨道平面，但对地球上的观测者来说，黄道面是最实用的。大部分在太阳系内的行星轨道平面对彼此之间和太阳赤道的倾角都很小。比较值得注意的例外是矮行星中的冥王星和阋神星，他们的倾角分别是17度和44度；还有小行星中的智神星倾角为34度。目前已知的许多系外行星，在多行星系统中也有一些是高倾角的。

卫星或人造卫星的倾角，如果与行星的距离够近，就会以它们所环绕的行星赤道面来测量，赤道平面是垂直于自转轴并通过中心的平面。

倾角0度的意义是环绕物体的轨道就在行星的赤道平面上，并且与行星运行的方向一致；

倾角90度是绕极的轨道，太空船会经过行星的南极和北极，另外；

倾角180度是在赤道平面上逆行的轨道。

如果物体离中心的天体很远，就需要使用另一种参考平面：拉普拉斯平面。在远离主星时，拉普拉斯平面从赤道平面分离开来，偏移的角度越来越大，直到与主星的轨道平面有最大的角距离。

对一个自转轴的方向不知道或是不明确的天体，一颗卫星的将以黄道面为量测的参考，有时（对移动缓慢的天体）会相对于天空的平面（参看下面对联星的定义）。

对月球，他的倾角是相对于地球的赤道平面，这导致他的数值变化迅速且变量很大，因此相对于黄道来测量会比较合理（这意味着月球是和地球一起绕着太阳转的），而且几乎就是一个常数值。

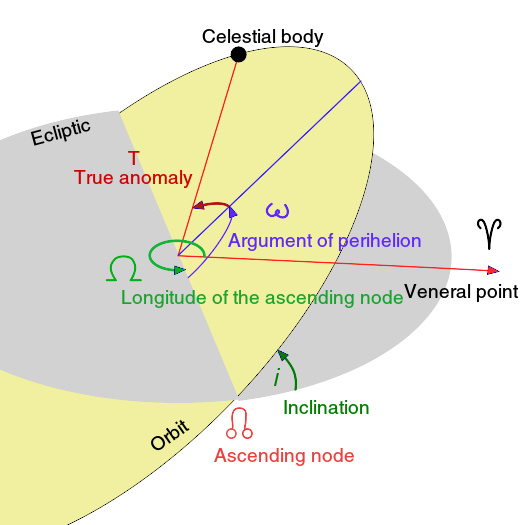
图一：倾角和其他的轨道参数。

其他意义

对行星和其它运转中的天体，自转轴的倾角是法线和轨道平面的角度，但使用转轴倾角（ axial tilt ）或倾斜度 （ obliquity ）意义会更加明确。

明确的说，对地球而言，对黄道的倾斜度是黄道面和赤道面之间的角度。

对在太阳系外天体的倾角，像是联星，因为没有其它的可以做为参考，就被定义为轨道平面（也就是轨道的轴）的法线与观测者方向所夹的角度。同样的，这也可以视为轨道平面和天空平面之间所夹的角度，因为后者也是依据观测者所住视的方向定义出来的，所以在比较天球上不同区域的恒星时要格外的小心。当联星的倾角接近90度（侧向时）经常会互食 。

计算

在太空动力学， 轨道倾角 i {\displaystyle i\,} 可以由下式算出：

i = arccos ⁡ ⁡ --> h z | h | {\displaystyle i=\arccos {h_{\mathrm {z} } \over \left|\mathbf {h} \right|}\,}

此处：

h z {\displaystyle h_{\mathrm {z} }\,} 是 h {\displaystyle \mathbf {h} \,} 在Z-方向上的分量

h {\displaystyle \mathbf {h} \,} 是垂直于轨道平面的轨道角动量向量。

相关条目

轴倾斜

古在机制

轨道倾角变化

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。