历史

莫里斯·弗雷歇在1906年于著作《Sur quelques points du calcul fonctionnel》, Rendic. Circ. Mat. Palermo 22(1906) 1–74 中引入了度量空间。

定义

度量空间是个有序对(M,d)，这里的 M 是集合而 d 是在 M 上的度量(metric)，即为函数

使得对于任何在 M 内的 x、y、z，下列条件均成立：

d(x, y) ≥ 0 (非负性)

d(x, y) = 0当且仅当x = y (不可区分者的同一性)

d(x, y) = d(y, x) (对称性)

d(x, z) ≤ d(x, y) + d(y, z) (三角不等式)。

条件 1 可由其他三个条件中导出。条件 1 做为度量空间的性质更恰当一些，但是很多课本都将其包含于定义之中。

函数 d 亦称为“距离函数”或简称“距离”。若依上下文可知道使用的度量为何，通常会省略 d，只写出 M 为度量空间。

若不考量数学上的细节，对于任何道路系统与地形，两个位置间之距离可被定义为连接这些位置的最短路径之长度。度量内不应该存在单行道。三角不等式表示每个弯路都不会是最短路径。下面的许多例子均可被视为此类一般概念的具体版本。

度量空间的例子

具有由绝对值给出的距离函数 d ( x , y ) = | y − − --> x | {\displaystyle d(x,y)=\vert y-x\vert }实数之实数集合，以及更一般性地欧几里得距离得距离之 n 维欧氏空间，这些空间均为完备度量空间。具有相关有理数有理数集合也会形成一个度量空间，但不完备。

具有距离函数 d ( x , y ) = | log ⁡ ⁡ --> ( y / x ) | {\displaystyle d(x,y)=\vert \log(y/x)\vert } 的正实数集合为完备度量空间。

双曲平面是个度量空间。

每个赋范向量空间都是度量空间，其度量可定义为 d ( x , y ) = ∥ ∥ --> y − − --> x ∥ ∥ --> {\displaystyle d(x,y)=\lVert y-x\rVert } 。若此类空间为完备的，则称之为巴拿赫空间。例如：

赋范向量空间上的英国铁路度量（亦称为邮局度量或法国铁路度量）定义为 d ( x , y ) = ∥ ∥ --> x ∥ ∥ --> + ∥ ∥ --> y ∥ ∥ --> {\displaystyle d(x,y)=\lVert x\rVert +\lVert y\rVert } ，其中 x 与 y 为不同的点，且 d(x,x) = 0。更一般性地， ∥ ∥ --> . ∥ ∥ --> {\displaystyle \lVert .\rVert } 可用由任意集合 S 映射至非负实数，且 0 至多出现一次的函数 f 替代：则集合 S 上的度量可定义为 d(x,y) = f(x) + f(y)，其中 x 与 y 为不同的点，且 d(x,x) = 0。此一度量的名称系用来影射不论旅途（或信件）的终点为何，都会经过伦敦（或巴黎）的情形。

若 (M, d) 为一度量空间，且 X 为 M 之子集，则 (X, d) 亦为一度量空间，且 d 的定义域缩限于 X × × --> X {\displaystyle X\times X} 。

离散度量，其中 d(x, y) = 0，若 x = y，不然 d(x, y) = 1。离散度量是个简单但重要的例子，可适用于任何非空集合。特别是，离散度量证明了对于任何非空集合，总是有一个度量空间与之关联。使用此一度量，每个点都是开球，且因此每个子集都是开放的，且该空间具有离散拓扑。

如果 X 是某个集合而 M 是度量空间，则由所有有界函数f : X → M（即那些像为 M 的有界子集之函数）所组成之集合，可透过定义对于任两个有限函数 f 与 g， d ( f , g ) = sup x ∈ ∈ --> X d ( f ( x ) , g ( x ) ) {\displaystyle d(f,g)=\sup _{x\in X}d(f(x),g(x))} （其中 sup {\displaystyle \sup } 为上确界），转换成度量空间。此一度量称之为一致度量或上确界度量，且若 M 为完备的，则此一函数空间亦为完备的。若 X 亦是个拓扑空间，则由所有从 X 至 M 连续函数续函数所组成之集合（具有一致度量），当 M 为完备时，该函数空间亦为完备的。

莱文斯坦距离是衡量两个字串u 与 v 间之差异的方法，定义为字串透过删除、插入或取代将 u 转变成 v 所需的最少步骤。该距离可被视为一个图中最短路径度量的特例，亦为编辑距离的一个例子。

如果 M 是连通黎曼流形，则通过把在两点之间的距离定义为连接两点的路径(连续可微曲线)之长度的下确界，将 M 变成度量空间。

如果 G 是无向连通图，则 G 的顶点集合 V 可通过定义 d(x, y) 为连接 x 的 y 的最短路径的长度，变成度量空间。在几何群论里，该度量可适用于一个群的凯莱图上，并称之为字度量。

类似的，在 3D 中在多面体的表面上的度量包括平常的度量，在表面上的距离；在多面体的边上第三个度量是路径为边的度量。例如，在单位立方体相对顶点之间的距离分别是 √3、√5 和 3。

如果 M 是度量空间，我们把 M 的所有紧致子集的集合 K(M) 变成度量空间，通过定义豪斯多夫距离d(X, Y) = inf{r : 对于所有 X 中的 x 存在 Y 中的 y 使得 d(x, y) < r, 并且对于所有 Y 中的 y 存在 X 中的 x 使得 d(x, y) < r)}。在这个度量中，两个元素是相互邻近的，如果一个集合的所有元素邻近于另一个集合某个元素。可以证明 K(M) 是完备的如果 M 是完备的。

所有紧致度量空间(的等距类)的集合形成了关于Gromov-豪斯多夫距离的度量空间。

给定度量空间 (X,d) 和递增凹函数 f:[0,∞)→[0,∞) 使得 f(x)=0 当且仅当 x=0，则 fod 也是 X 上的度量。

给定从任何集合 A 到度量空间 (X,d) 的单射函数 f，d(f(x), f(y)) 定义了在 A 上的度量。

使用T-理论，度量空间的紧跨越(tight span)也是度量空间。紧跨越在多种类型的分析中都有用处。

由某些域上的所有 n×m 矩阵所组成之集合，是个具有秩距离 d(X,Y) = rank(Y-X) 的度量空间。

赫吕度量用于赛局理论里。

开集、闭集、拓扑与收敛性

每个度量空间都自然地会是个拓扑空间，且因此与一般拓扑空间有关的所有定义及定理也一样适用于所有的度量空间。

对于度量空间 M 内的任一点 x，可定义中心为 x，半径为 r > 0（其中，r 为一实数）的开球

这些开球会形成 M 上拓扑的基，使之成为一个拓扑空间。

具体来说，M 的子集 U 称之为开放的，若对于每个 U 内的 x，存在一个 r > 0，使得 B ( x ; r ) {\displaystyle B(x;r)} 包含于 U。开集的补集为闭集。点 x 的邻域是指 M 内包含中心为 x 的某一开球之任何子集。

拓扑空间若可由某个度量空间形成，则称之为可度量化空间；更进一步的细节请见乌雷松度量化定理。

度量空间 M 内之序列( x n {\displaystyle x_{n}} ) 称之为可收敛至极限 x ∈ ∈ --> M {\displaystyle x\in M} ，当且仅当对于每个 ϵ ϵ --> > 0 {\displaystyle \epsilon >0} ，均存在一个自然数 N，使得 d ( x n , x ) {\displaystyle d(x_{n},x) ，对于所有 n > N。在拓扑空间内也有相对应的收敛之一般定义。

度量空间 M 内的子集 A 是封闭的，当且仅当每个在 A 内的序列若可收敛至 M 内的一极限，则该极限在 A 内。

度量空间的类型

完备空间

度量空间 M 称之为完备的，若每个柯西序列均收敛于 M 内，亦即：若 d ( x n , x m ) → → --> 0 {\displaystyle d(x_{n},x_{m})\to 0} ，其中 n 与 m 个自趋近于无限大，则存在某个 y ∈ ∈ --> M {\displaystyle y\in M} ，使得 d ( x n , y ) → → --> 0 {\displaystyle d(x_{n},y)\to 0} 。

每个欧氏空间都是完备的，而且该空间的每个闭子集也都是完备空间。使用绝对值度量 d ( x , y ) = | x − − --> y | {\displaystyle d(x,y)=\vert x-y\vert } 的有理数集合则不是完备的。

每个度量空间都有个在同构意义下唯一的完备化空间。该完备化空间是个完备空间，给定之度量空间为其稠密子集。例如，实数是有理数的完备化空间。

若 X 是空间空间 M 内的完备子集，则 X 在 M 内是封闭的。而实际上，一个空间是完备的，当且仅当该空间在任何包含该空间的度量空间内都是封闭的。

每个完备度量空间都是个贝尔空间。

有界与完全有界空间

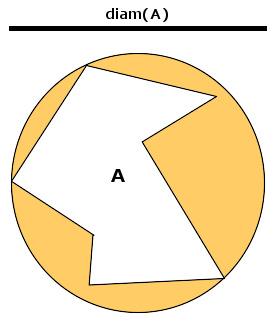
  一个集合的直径。

度量空间 M 被称为有界的，如果存在某个数 r，使得对于所有 M 中的 x 和 y 有 d(x,y) ≤ r。r 最小可能的值称之为 M 的直径。空间 M 称之为预紧致的或完全有界的，如果对于所有 r > 0 存在有限多个半径为 r 的开球，其并集覆盖 M。因为这些球为有限个，所以该空间的直径亦为有限值，从而得出(使用三角不等式)所有完全有界空间都是有界的。但逆命题不成立，因为任何无限集合均可给定其离散度量(上面第一个例子)，使得该空间是有界的，但不是完全有界的。

须注意，在讨论实数空间的区间及欧氏空间的区域时，有时会将有界集合指为“有限区间”或“有限区域”。不过，有界性与“有限”之间一般并无关连；有限通常意含着有界，但反之不一定成立。

紧致空间

度量空间 M 是紧致的，若每个 M 内的序列均有个子序列，会收敛于 M 内的一点。这称为序列紧致性，且在度量空间（但不是一般拓扑空间）里，这等价于可数紧致与以开覆盖定义之紧致性等拓扑性质。

紧致度量空间的例子包括具绝对值度量的闭区间 [0,1]、所有具有限多个点的度量空间，以及康托尔集。每个紧致集合的闭子集亦是紧致的。

一度量空间为紧致的，当且仅当该空间是完备的，且为完全有界的。这即是所谓的海涅－博雷尔定理。须注意，紧致性仅决取于拓扑，而有界性则决取于度量。

勒贝格数引理表示，对于紧致度量空间 M 内的每个开覆盖，均存在一个“勒贝格数”δ，使得每个 M 内直径< δ 的子集均会被包含于某些覆盖内。

每个紧致度量空间均为第二可数，且是康托尔集的连续像。（后者由帕维尔·亚历山德罗夫与帕维尔·萨穆伊洛维奇·乌雷松所证得。）

局部紧致与常态空间

度量空间M称为局部紧致的，如果每一点都有一个紧致邻域。欧氏空间为局部紧纱的，但无限维巴拿赫空间则不是。

度量空间M称为常态（proper）的，如果每个闭球都是紧致的。常态空间是完备且局部紧致的，但局部紧致空间未必是常态的。

连通性

度量空间 M 是连通的，若唯一同时开放或封闭的子集只有空集与 M 本身。

度量空间 M 是路径连通的，若对于 M 内的任两点 x、y，均存在一个连续映射 f : : --> [ 0 , 1 ] → → --> M {\displaystyle f\colon [0,1]\to M} ，其中 f(0)=x 且 f(1)=y。每个路径连通空间都是连通的，但反之通常不成立。

上述性质均有相对的局部定义：局部连通空间与局部路径连通空间。

单连通空间在某一层面上来说，可说是个没有“洞”的空间。

可分空间

一度量空间称之为可分空间，若该空间有可数稠密子集。典型的例子为实数或任何一个欧氏空间。对于度量空间（但不包括一般拓扑空间）可分性等价于第二可数，亦等价于林德勒夫性质。

度量空间之间的映射类型

假设 (M1,d1) 与 (M2,d2) 为两个度量空间。

连续映射

映射 f:M1→M2 是连续的，若具有下列一个（因此所有）等价性质：

这是在拓扑学里连续性的一般定义。

这是由爱德华·海涅所提出的序列连续性。

这用到了极限的(ε, δ)定义，由奥古斯丁·路易·柯西所提出。

此外，f 是连续的，当且仅当该函数在 M1 的每个紧致子集内都是连续的。

每个紧致集合在连续函数下的像亦是紧致的，且每个连通集合在连续函数下的像亦是连通的。

一致连续映射

映射 ƒ : M1 → M2 为一致连续的，若对于每个 ε > 0，均存在 δ > 0，使得

每个一致连续映射 ƒ : M1 → M2 均是连续的。若 M1 是紧致的，则反向的陈述亦会成立。（海涅－康托尔定理）

一致连续映射会将 M1 内的柯西序列转换成 M2 内的柯西序列。对于连续映射，该陈述则不一定会成立；例如，一个将开区间 (0,1) 满射至实数线的连续映射即会将柯西序列转换成无界的序列。

利普希茨连续映射与压缩映射

给定一数 K > 0，映射 ƒ : M1 → M2 为利普希茨连续，若

每个利普希茨连续映射均是一致连续的，但反之不一定成立。

若 K < 1，则 f 称之为压缩映射。令 M2 = M1，且 M1 是完备的。若 f 是个压缩映射，则 f 会有个唯一的不动点（巴拿赫不动点定理）。若 M1 是紧致的，则条件可稍微放宽一点：f 会有个唯一的不动点，若

等距同构

映射 f:M1→M2 称之为等距同构，若

等距同构总会是单射的；紧致或完备集合在等距同构下的像仍分别会是紧致或完备的。不过，若等距同构不是满射的，则闭（或开）集的像不一定是封闭（或开放）的。

拟等距同构

映射　f : M1 → M2　称之为拟等距同构，若存在常数 A ≥ 1 与 B ≥ 0，使得

且有一个常数 C ≥ 0，使得 M2 内的每个点与像 f(M1) 内的某个点间之距离至多为 C。

须注意，拟等距同构不需要是连续的。拟等距同构比较度量空间的“大尺度结构”；多用于几何群论内与字度量有关的理论。

度量空间等价性的概念

度量空间之间有着不同的等价性。依据两个空间之间能够存在的函数，可给出不同等价的程度与类型。

给定两个度量空间 (M1, d1) 和 (M2, d2):

这两个空间称之为同胚（拓扑同构）的，若存在两者间的同胚（即两个方向均为连续的双射）。在此条件下，这两个空间能导出相同的拓扑空间。

这两个空间称之为一致同构的，若存在两者间的一致同构（即两个方向均为一致连续的双射）。

这两个空间称之为等距同构的，若存在两者间的等距同构双射。在此一条件下，两个度量空间基本上是相同的。

这两个空间称之为拟等距同构的，若存在两者间的拟等距同构。

拓扑性质

度量空间是个仿紧致豪斯多夫空间，因此是个正规空间（且实际上是个完美正规空间）。度量空间也是个第一可数空间，因为可使用具有理数半径的球作为该空间的基。

依据提策扩展定理，每个度量空间都能具有单位分解，且每个定义于度量空间的闭子集上之连续实数值函数均能扩展成整个空间的连续映射。每个定义于度量空间的子集上之实数值利普希茨连续映射亦能扩展成整个空间的利普希茨连续映射。

度量空间 M 上的度量拓扑是使得 M × × --> M {\displaystyle M\times M} 映射至非负实数的度量 d 为连续之最粗糙拓扑。

点和集合间的距离

构造分离一个点与一个闭集的函数(作为完全正则空间的要求)的简单方式是考虑点和集合之间的距离。 如果 (M,d) 是度量空间，S 是 M 的子集而 x 是 M 的点，则可定义从 x 到 S 的距离为

d(x, S) = 0 当且仅当 x 包含于 S 的闭包内。此外，可将三角不等式推广如下：

其中，可证明映射 x ↦ ↦ --> d ( x , S ) {\displaystyle x\mapsto d(x,S)} 是连续的。

给定两个 M 内的子集 S 与 T，可定义豪斯多夫距离为

一般而言，豪斯多夫距离 dH(S,T) 可以是无限大的。两个集合的在豪斯多夫距离上会互相靠近，若其中一个集合的每个元素会靠近另一集合的某个元素。

豪斯多夫距离 dH 会将由所有 M 内非空紧致子集所组成之集合 K(M) 转换成一个度量空间。可证明若 M 是完备的，则 K(M) 亦是完备的。（紧致子集的收敛性亦可由库拉托夫斯基收敛给出。）

然后，可定义任两个度量空间之间的格罗莫夫-豪斯多夫距离为这两个空间的等距同构嵌入版本间之最短豪斯多夫距离。使用此一距离，由所有（等距同构类型的）紧致度量空间所组成的类本身即会形成一个度量空间。

积度量空间

如果 ( M 1 , d 1 ) , … … --> , ( M n , d n ) {\displaystyle (M_{1},d_{1}),\ldots ,(M_{n},d_{n})} 是度量空间，而 N 是在 R 上的欧几里得范数，则 ( M 1 × × --> … … --> × × --> M n , N ( d 1 , … … --> , d n ) ) {\displaystyle {\Big (}M_{1}\times \ldots \times M_{n},N(d_{1},\ldots ,d_{n}){\Big )}} 亦为度量空间，且积度量定义为

积度量导出之拓扑等价于积拓扑。依据有限维的范数之等价性，曼哈顿范数、p-范数、最大范数，及其他当座标内的分量增加时不会减少（符合三角不等式）之范数，所给出的度量均为拓扑同构。

同样的，度量空间的可数积度量可以定义为如下度量：

度量空间的不可数积度量不一定是可度量化的。例如， R R {\displaystyle \mathbf {R} ^{\mathbf {R} }} 不是第一可数空间，因此不能度量化。

距离的连续性

值得注意的是，在一个空间 ( M , d ) {\displaystyle (M,d)} 中，距离映射 d : M × × --> M → → --> R + {\displaystyle d:M\times M\rightarrow R^{+}} 在上述任何一个积度量 N ( d , d ) {\displaystyle N(d,d)} 下均是一致连续的，且特别是，在 M × × --> M {\displaystyle M\times M} 下的积拓扑会是连续的。

商度量空间

若 M 为度量空间，其度量为 d，且 ~ 为 M 上之等价关系，则可在商集合 M/~ 上赋加下面的（伪）度量。给定两个等价类 [x] 与 [y]，可定义

其中， [ p 1 ] = [ x ] {\displaystyle [p_{1}]=[x]} 、 [ q i ] = [ p i + 1 ] {\displaystyle [q_{i}]=[p_{i+1}]} 、 [ q n ] = [ y ] {\displaystyle [q_{n}]=[y]} （即取从 [x] 至 [y] 经过所有等价类之路径的最短长度）。一般来说，这仅能定义出一个伪度量，即 d"([x],[y])=0 不一定蕴涵 [x] = [y]。不过，对于良好的等价关系（如将多面体沿着面胶合），则会是个度量。此外，若 M 是个紧致空间，则该度量在 M/~ 上导出之拓扑为商拓扑。

商度量 d 具有下列泛性质：若 f : ( M , d ) ⟶ ⟶ --> ( X , δ δ --> ) {\displaystyle f:(M,d)\longrightarrow (X,\delta )} 是个度量空间之间的度量映射（英语：metric map）（即对于所有 x、y， δ δ --> ( f ( x ) , f ( y ) ) ≤ ≤ --> d ( x , y ) {\displaystyle \delta (f(x),f(y))\leq d(x,y)} ），满足当 x ∼ ∼ --> y , {\displaystyle x\sim y,} 时，f(x)=f(y) 的条件，则函数 f ¯ ¯ --> : : --> M / ∼ ∼ -->⟶ ⟶ --> X {\displaystyle {\overline {f}}\colon M/\sim \longrightarrow X} 定义为 f ¯ ¯ --> ( [ x ] ) = f ( x ) {\displaystyle {\overline {f}}([x])=f(x)} ，亦会是个度量映射 f ¯ ¯ --> : : --> ( M / ∼ ∼ --> , d ′ ) ⟶ ⟶ --> ( X , δ δ --> ) {\displaystyle {\overline {f}}\colon (M/\sim ,d")\longrightarrow (X,\delta )} 。

一个拓扑空间是序列的，当且仅当该空间是个度量空间的商空间。

度量空间的推广

每个度量空间都自然会是个一致空间，而每个一致空间也都自然会是个拓扑空间。因此，一致空间与拓扑空间均可视为度量空间的推广。

若考量上面给定之度量空间的第一个定义，放宽定义中的第二个条件，则可得到伪度量空间。若移除第三个或第四个条件，则可分别得到拟度量空间与半度量空间。

若距离函数的对应域为扩展实数线R∪{+∞}，定义中的四个条件维持不变，则称该空间为“扩展度量空间”或“ ∞ ∞ --> {\displaystyle \infty } -度量空间”。若距离函数的对应域为某个（适当的）有序集（且三角不等式有对应的调整），则可得出“扩展超度量”这个概念。

趋近空间（英语：Approach space）是度量空间的推广，以点对集合的距离取代点对点的距离。

连续性空间是度量空间与偏序集的推广，用来统整度量空间与域的概念。

部分度量空间是为了对度量空间作最小化的推广，使得每个点对自身的距离不再一定为零。

度量空间作为丰富范畴

有序集 ( R , ≥ ≥ --> ) {\displaystyle (\mathbb {R} ,\geq )} 可透过令 a ≥ ≥ --> b {\displaystyle a\geq b} 时恰有一态射 a → → --> b {\displaystyle a\to b} ，否则没有范畴，将之视为一个范畴。使用 + 作单位元积，0 作为单位元，该集合可变成一个幺半范畴 R ∗ ∗ --> {\displaystyle R^{*}} 。每个度量空间 (M, d) 均可被视为 R ∗ ∗ --> {\displaystyle R^{*}} 上的丰富范畴 M ∗ ∗ --> {\displaystyle M^{*}} 。其步骤如下：

令 Ob ⁡ ⁡ --> ( M ∗ ∗ --> ) := M {\displaystyle \operatorname {Ob} (M^{*}):=M} （M 内的元素为丰富范畴 M ∗ ∗ --> {\displaystyle M^{*}} 之物件）。

对于每个 M 内的元素 X、Y，令 Hom ⁡ ⁡ --> ( X , Y ) := d ( X , Y ) ∈ ∈ --> Ob ⁡ ⁡ --> ( R ∗ ∗ --> ) {\displaystyle \operatorname {Hom} (X,Y):=d(X,Y)\in \operatorname {Ob} (R^{*})} （M 的度量为丰富范畴 M ∗ ∗ --> {\displaystyle M^{*}} 之态射）。

态射复合 Hom ⁡ ⁡ --> ( Y , Z ) ⊗ ⊗ --> Hom ⁡ ⁡ --> ( X , Y ) → → --> Hom ⁡ ⁡ --> ( X , Z ) {\displaystyle \operatorname {Hom} (Y,Z)\otimes \operatorname {Hom} (X,Y)\to \operatorname {Hom} (X,Z)} 亦为 R ∗ ∗ --> {\displaystyle R^{*}} 内的唯一态射，因为三角不等式 d ( y , z ) + d ( x , y ) ≥ ≥ --> d ( x , z ) {\displaystyle d(y,z)+d(x,y)\geq d(x,z)} 。

单位态射 0 → → --> Hom ⁡ ⁡ --> ( X , X ) {\displaystyle 0\to \operatorname {Hom} (X,X)} 是唯一的，因为 0 ≥ ≥ --> d ( X , X ) {\displaystyle 0\geq d(X,X)} 。

参见

三角不等式

利普希茨连续

等距同构，压缩映射和度量映射

范数

参考资料

Dmitri Burago, Yu D Burago, Sergei Ivanov. A Course in Metric Geometry. American Mathematical Society. 2001. ISBN 0-8218-2129-6. 

Victor Bryant. Metric Spaces: Iteration and Application. Cambridge University Press. ISBN 0-521-31897-1. 

Mícheál Ó Searcóid.Metric Spaces. Springer Undergraduate Mathematics Series. 2006. ISBN 1-84628-369-8. 

Athanase Papadopoulos. Metric Spaces, Convexity and Nonpositive Curvature 2nd.European Mathematical Society. 2014. ISBN 978-3-03719-132-3. 

Lawvere, F. William.Metric spaces, generalized logic, and closed categories. Reprints in Theory and Applications of Categories. 2002, 1: 1–37. 

MathWorld上Metric Space的资料，作者：埃里克·韦斯坦因。

MathWorld上Product Metric的资料，作者：埃里克·韦斯坦因。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。