各级反应

表中， M {\displaystyle \ M} 代表摩尔浓度 m o l / L {\displaystyle \ mol/L} ， t {\displaystyle \ t} 代表时间， k {\displaystyle \ k} 代表反应的速率常数。所说的“二级反应”和“ n {\displaystyle \ n} 级反应”指的是纯级数反应，也就是反应速率只与一个反应物的二次方或 n {\displaystyle \ n} 成正比。

可逆反应

可逆反应（又称平衡反应、对行反应、对峙反应）指的是反应物与产物形成化学平衡的反应，其中正向和逆向反应同时进行，而且反应速率相等。它可以用下面的方程式来表示：

假设正向反应速率为 k 1 {\displaystyle \ k_{1}} ，逆向反应速率为 k − − --> 1 {\displaystyle \ k_{-1}} 。因此，正向反应的净速率是正、逆反应速率的代数和，即：

k 1 {\displaystyle \ k_{1}} 与 k − − --> 1 {\displaystyle \ k_{-1}} 又恰好能与平衡常数衡常数 K {\displaystyle \ K} 通过下列关系联系起来：

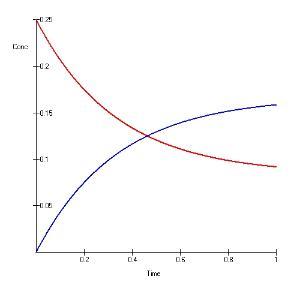
 A ( A 0 = 0.25 M {\displaystyle \ A(A_{0}=0.25M} ) 与 B {\displaystyle \ B} 发生的可逆反应的 c − − --> t {\displaystyle \ c-t} 图。正向和逆向反应的速率分别为 2 m i n − − --> 1 {\displaystyle \ 2min^{-1}} 和 1 m i n − − --> 1 {\displaystyle \ 1min^{-1}} 。可以看出，经过足够长的时间，可逆反应中的反应物和产物都要分别趋近它们的平衡浓度。

下面讨论一个简单的单分子可逆一级反应：

达到平衡时的平衡常数 K {\displaystyle \ K} 可以表示为：

其中， [ A ] e {\displaystyle \ [A]_{e}} 和 [ B ] e {\displaystyle \ [B]_{e}} 分别为 A {\displaystyle \ A} 和 B {\displaystyle \ B} 的平衡浓度。假设， B {\displaystyle \ B} 的初始浓度 [ B ] 0 = 0 {\displaystyle \ [B]_{0}=0} ，而且达到平衡时，反应物 A {\displaystyle \ A} 已反应成 B {\displaystyle \ B} 的浓度为 X {\displaystyle \ X} ，于是有：

代入上面的定义式：

整理得：

A {\displaystyle \ A} 的净消耗速率为：

t = ∞ ∞ --> {\displaystyle \ t=\infty } 时，反应达到平衡， A {\displaystyle \ A} 的净消耗速率为零，即：

上上式减上式，可得：

当 [ A ] 0 {\displaystyle \ [A]_{0}} 一定时， [ A ] e {\displaystyle \ [A]_{e}} 为常量，于是有：

将上式代入上上式，得：

进行分离变数积分，可以得到：

从上式可以看出，平衡反应的 ln ⁡ ⁡ --> ( [ A ] − − --> [ A ] e ) − − --> t {\displaystyle \ \ln {([A]-[A]_{e})}-t} 图为一直线，由直线斜率可求出 k 1 + k − − --> 1 {\displaystyle \ k_{1}+k_{-1}} ，然后再根据实验测得的 A e {\displaystyle \ A_{e}} ／ B e {\displaystyle \ B_{e}} ，就可以求得 K {\displaystyle \ K} 和 k 1 k − − --> 1 {\displaystyle \ {\frac {k_{1}}{k_{-1}}}} ，与上面的 k 1 + k − − --> 1 {\displaystyle \ k_{1}+k_{-1}} 联立便可以解出 k 1 {\displaystyle \ k_{1}} 和 k − − --> 1 {\displaystyle \ k_{-1}} 。

或者，将 x {\displaystyle \ x} 定义为反应后某一时刻已经转化为 B {\displaystyle \ B} 的 A {\displaystyle \ A} 的浓度，则：

整理，可得某一时刻反应物 A {\displaystyle \ A} 的浓度 [ A ] t {\displaystyle \ [A]_{t}} 的表达式：

t = ∞ ∞ --> {\displaystyle \ t=\infty } 时，得到 [ A ] e = k − − --> 1 [ A ] 0 k 1 + k − − --> 1 {\displaystyle \ [A]_{e}={\frac {k_{-1}[A]_{0}}{k_{1}+k_{-1}}}} ，与上面的结果相吻合。将这些结果代入 ln ⁡ ⁡ --> ( [ A ] 0 − − --> [ A ] e [ A ] t − − --> [ A ] e ) {\displaystyle \ \ln({\frac {[A]_{0}-[A]_{e}}{[A]_{t}-[A]_{e}}})} ，化简之后得到 ( k 1 + k − − --> 1 ) t {\displaystyle \ (k_{1}+k_{-1})t} ，与上面(1)式结果相同。

为了求得反应的半衰期，令 [ A ] t = 1 2 [ A ] 0 {\displaystyle \ [A]_{t}={\frac {1}{2}}[A]_{0}} ，将其代入上面(1)式或(2)式，可以得到：

如果反应的 K {\displaystyle \ K} 值很大，那么 k 1 >> k − − --> 1 {\displaystyle \ k_{1}>>k_{-1}} ， t 1 2 = 1 k 1 + k − − --> 1 ln ⁡ ⁡ --> 2 {\displaystyle \ t_{\tfrac {1}{2}}={\frac {1}{k_{1}+k_{-1}}}\ln {2}} 。

可以看出，平衡反应中的半衰期与反应物的初始浓度无关。

对行反应的例子有：

乙酸和乙醇的酯化反应： C H 3 C O O H + C 2 H 5 O H ⇌ ⇌ --> C H 3 C O O C 2 H 5 + H 2 O {\displaystyle \ CH_{3}COOH+C_{2}H_{5}OH\rightleftharpoons CH_{3}COOC_{2}H_{5}+H_{2}O}

邻苯二甲酸酐与异辛醇反应生成邻苯二甲酸二异辛酯的反应。

连续反应

连续反应（又称串联反应、连串反应）指的是如下类型的化学反应：

第一个反应产生的 B {\displaystyle \ B} 又可以再起反应生成 C {\displaystyle \ C} 。反应的速率方程一般形式为：

对 ( 3 ) {\displaystyle \ (3)} 式积分，得：

将 ( 6 ) {\displaystyle \ (6)} 式代入 ( 4 ) {\displaystyle \ (4)} 式，得：

对其进行积分：

由于

将 ( 6 ) {\displaystyle \ (6)} 和 ( 7 ) {\displaystyle \ (7)} 式代入，可得：

这样， [ A ] {\displaystyle \ [A]} 、 [ B ] {\displaystyle \ [B]} 、 [ C ] {\displaystyle \ [C]} 三个浓度就都可以求出了。如果中间体 B {\displaystyle \ B} 是目标产物，则 [ B ] {\displaystyle \ [B]} 达到最大值时（最佳时间）就必须终止反应。通过将 ( 7 ) {\displaystyle \ (7)} 式对 t {\displaystyle \ t} 取导数，令其为0，可以求出中间体 B {\displaystyle \ B} 的最佳时间 t max {\displaystyle \ t_{\mbox{max}}} 和 B {\displaystyle \ B} 的最大浓度 [ B ] max {\displaystyle \ [B]_{\mbox{max}}} ：

用稳态近似法分析也可以取得类似的结果。

连续反应的例子有：

丙烯被氧气氧化为丙酮、乙酸的反应： 丙烯 → O 2 {\displaystyle \ \ {\xrightarrow {O_{2}}}\ } 丙酮 → O 2 {\displaystyle \ \ {\xrightarrow {O_{2}}}\ } 乙酸

4-氨基偶氮苯用发烟硫酸磺化时发生的反应： 4－氨基偶氮苯 → H 2 S O 4 {\displaystyle \ \ {\xrightarrow {H_{2}SO_{4}}}\ } 一磺化物 → H 2 S O 4 {\displaystyle \ \ {\xrightarrow {H_{2}SO_{4}}}\ } 二磺化物

平行反应

平行反应（又称竞争反应）指的是同一反应物可以同时进行几种不同的反应，生成不同的产物。

如果两个平行反应都是一级反应，则三个速率方程分别为：

对其积分可以得到 [ A ] {\displaystyle \ [A]} 、 [ B ] {\displaystyle \ [B]} 和 [ C ] {\displaystyle \ [C]} 的表达式：

一个比较重要的关系式是： [ B ] [ C ] = k 1 k 2 {\displaystyle {\frac {[B]}{[C]}}={\frac {k_{1}}{k_{2}}}} ，即任一瞬间两产物浓度之比都等于两反应速率常数之比。

两个平行反应分别为一级和二级反应：

想象下面的情形：反应物 A {\displaystyle \ A} 在发生二级反应 A + R → → --> C {\displaystyle A+R\rightarrow C} 的同时，还有少量 A {\displaystyle \ A} 发生水解（可以看作准一级反应）： A + H 2 O → → --> B {\displaystyle A+H_{2}O\rightarrow B} 。因此，反应的速率方程为：

通过假设 [ A ] 0 − − --> [ C ] ≈ ≈ --> [ A ] 0 {\displaystyle [A]_{0}-[C]\approx \;[A]_{0}} ，在对上述式子积分后，可以得出主要产物 C {\displaystyle \ C} 的浓度 [ C ] {\displaystyle \ [C]} 和副产物 B {\displaystyle \ B} 的浓度 [ B ] {\displaystyle \ [B]} ：

以上只是几种基本的复合反应类型，除此以外，还有很多情况是上述几种基本复合反应的混合。请有兴趣的读者参见酶动力学、米氏方程和酶抑制剂等文章。

速率方程的确定

速率方程的确定主要有以下三种方式：

微分法：对 − − --> d [ A ] d t = k [ A ] n {\displaystyle \ -{\frac {d[A]}{dt}}=k[A]^{n}} 求对数，得到： ln ⁡ ⁡ --> ( d [ A ] d t ) = ln ⁡ ⁡ --> k + n ln ⁡ ⁡ --> [ A ] {\displaystyle \ \ln {({\frac {d[A]}{dt}})}=\ln {k}+n\ln {[A]}} ，然后取若干个不同的初始浓度 [ A ] 0 {\displaystyle \ [A]_{0}} ，分别从 [ A ] − − --> t {\displaystyle \ [A]-t} 图上求出相应的斜率 d [ A ] 0 d t {\displaystyle \ {\frac {d[A]_{0}}{dt}}} ，求出 ln ⁡ ⁡ --> ( − − --> d [ A ] 0 d t ) − − --> ln ⁡ ⁡ --> [ A ] 0 {\displaystyle \ \ln {(-{\frac {d[A]_{0}}{dt}})}-\ln {[A]_{0}}} 直线的斜率，并进一步求出反应物 A {\displaystyle \ A} 的反应级数。

尝试法／试差法：分别将某一化学反应的 [ A ] {\displaystyle \ [A]} 和 t {\displaystyle \ t} 代入各种级数反应的积分速率方程，看哪一个最准确。

半衰期法：求得两个不同初始浓度下的反应半衰期，然后根据总结一节中的半衰期通式，求出反应级数。

参见

反应速率

速率常数

平衡态近似、稳态近似

表面化学反应

参考资料

^IUPAC金皮书对“反应速率”（rate law）的定义：[1]。

^ Connors, Kenneth A. Chemical Kinetics, the study of reaction rates in solution. VCH Publishers. 1991.

^ Rushton, Gregory T.; William G. Burns, Judi M. Lavin, Yong S. Chong, Perry Pellechia, Ken D. Shimizu. Determination of the Rotational Barrier for Kinetically Stable Conformational Isomers via NMR and 2D TLC - An Introductory Organic Chemistry Experiment. J. Chem. Educ. 2007, 84 (1499). .Abstract.

^ Manso, José A.; et al. . A Kinetic Approach to the Alkylating Potential of Carcinogenic Lactones. Chem. Res. Toxicol. 2005, 18 (7): 1161-1166.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。