二维空间

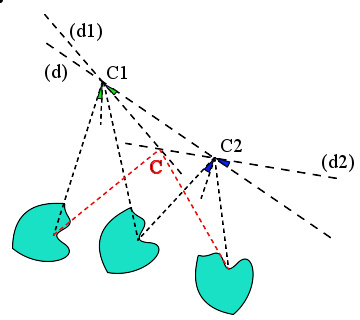
在绕一个点旋转之后绕另一个不同的点的平面旋转导致要么是旋转（如本图）要么是平移的一个总和运动。

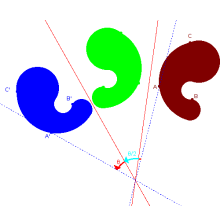
在针对一个轴的反射之后的针对不平行于前一个轴的反射导致是绕两个轴的交点的旋转的一个总和运动。

在讨论旋转的时候理解参照系是重要的。一种观点来看，你可以保持坐标轴固定旋转向量。而从另一观点出发，你可以保持向量固定旋转坐标系。

在第一种观点看来， 坐标 或 向量 关于原点的逆时针旋转；或者从第二种观点看来， 平面 或 轴 关于原点的顺时针旋转。这里的 ( x , y ) {\displaystyle (x,y)} 被旋转了 θ θ --> {\displaystyle \theta } 并希望知道旋转后的坐标 ( x ′ , y ′ ) {\displaystyle (x",y")} :

或

平面 或 轴 关于原点的逆时针旋转，在新平面中的坐标将顺时针旋转到旧坐标。在这种情况下，如果在旧平面中的坐标是 ( x , y ) {\displaystyle (x,y)} ，同一个向量在新平面中的坐标是 ( x ′ , y ′ ) {\displaystyle (x",y")} ，则：

或

向量( x , y )的大小同于向量 ( x ′, y ′)的大小。

复平面

复数可以看作是在复平面中的二维向量，它的尾部在原点而头部由这个复数给出。设

是这样一个复数。它的实部是横坐标而虚部是纵坐标。

则 z 可逆时针旋转角度θ，通过乘以 e i θ θ --> {\displaystyle e^{i\theta }} （参见欧拉公式, §2）。

这可以被看作对应于在§ 1中描述的旋转。

因为复数的乘法是交换性的，不同于在更高维中的情况，二维旋转是可交换的。

三维空间

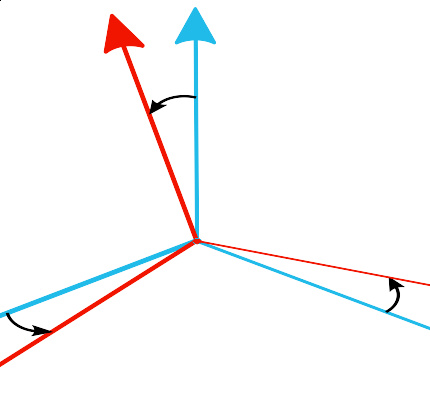
旋转描述刚体围绕一个点的运动。

在普通三维空间中，坐标旋转可以用欧拉角来定义，或关于要绕其旋转的向量和一个单一的旋转角度构成的轴角定义。

关于原点的旋转最容易使用叫做旋转矩阵的3×3矩阵变换来计算。关于其他点的旋转可以使用表现齐次坐标的4×4矩阵来描述。

四元数

表现在三维空间中的旋转的一种可供选择的方式是四元数。

四元数提供了表示在三维中旋转和方向的另一种方式。它们应用与计算机图形学、控制理论、信号处理和轨道力学中。例如，在太空船的姿态控制系统中常用四元数来下达指令，还用于测距它们的当前姿态。基本原理是组合很多四元数变换比组合很多矩阵变换在数值上更加稳定。

一般化

正交矩阵

描述旋转的所有矩阵的集合 M( v ,θ) 加上矩阵乘法运算叫做旋转群：SO(3)。

引用

Hestenes, David. New Foundations for Classical Mechanics. Dordrecht: Kluwer Academic Publishers. 1999. ISBN 0-7923-5514-8.

Lounesto, Pertti. Clifford algebras and spinors. Cambridge: Cambridge University Press. 2001. ISBN 978-0-521-00551-7.

参见

旋转表示

自旋

欧拉角

旋涡

旋转群

坐标旋转和反射

Rodrigues旋转公式

旋转矩阵

方向 (几何)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。