历史

  艾蒂安-路易·马吕斯

丹麦科学家拉斯穆·巴多林（Rasmus Bartholin）于1669年发现了光束通过冰洲石（Iceland spar）时会出现双折射现象，假设照射光束于冰洲石，则这光束会被折射为两道光束，一道光束遵守普通的折射定律，称为“寻常光”，另外一道光束不遵守普通的折射定律，称为“非常光”。巴多林无法解释这现象的物理机制。 后来，克里斯蒂安·惠更斯注意到这奇特现象，他在1690年著作《光论》的后半部里，对这现象有很详细的论述；他认为，由于空间可能存在有两种不同物质，所以才会出现两道光束，它们分别对应于两个不同的波前以不同的速度传播于空间，所以，这不是很不平常的现象，但是，惠更斯又发现，这两道光束与原本光束的性质大不相同，将其中任何一道光束照射于第二块冰洲石，则折射出来的两道光束，其辐照度会因为绕着光束轴旋转冰洲石而改变，有时候甚至只会剩成一道光束。惠更斯猜想光波是纵波，他想出的简单波动理论不能对这现象给出解释。艾萨克·牛顿猜测，双折射现象意味着组成光束的粒子具有侧面（垂直于移动方向）性质。

1808年，法兰西学术院提议，1810年物理奖比赛的题目为“对于双折射给出数学理论，并且做实验证实”。艾蒂安-路易·马吕斯决定参与竞争。他做实验观察，日光照射于卢森堡宫的玻璃窗，然后被玻璃反射出来的光束，假若入射角度达到某特定数值，则这反射光与惠更斯观察到的折射光具有类似的性质，他称这性质为“偏振”性质。他猜想，组成光束的每一道光线都具有某种特别的不对称性；当这些光线具有相同的不对称性时，则光束具有偏振性；当这些光线的不对称性分别概率地指向不同方向时，则光束具有非偏振性；当在这两种案例之间时，则光束具有部分偏振性。不单是玻璃，任何透明的固体或液体都会产生这种现象。他又从实验结果推论出马吕斯定律，定量地给出偏振光通过检偏器后的辐照度，考虑到偏振方向与检偏器传输轴方向之间的夹角角度。这实验极具创意，又得到了很丰硕的重要成果，马吕思因此荣获1810年的物理奖。马吕思对于偏振现象做出诸多贡献，后人尊称他为“偏振之父”。

后来，奥古斯丁·菲涅耳与弗朗索瓦·阿拉戈合作研究偏振对于杨氏干涉实验的影响，他们认为光波是纵波，呈纵向震荡，但是这纵波的概念无法合理解释实验结果。阿拉戈告诉托马斯·杨这问题，托马斯·杨大胆建议，假若光波是横波，呈横向震荡，则光波可以分解为两个相互垂直的分量，或许这样做可以对实验结果给出解释。果真，这建议清除了很多疑点。1817年，菲涅耳与阿拉戈将实验结果定性总结为菲涅耳-阿拉戈定律（Fresnel-Arago laws），表述处于不同偏振态的光束彼此之间的干涉性质。之后，菲涅耳试图进一步定量表述这实验，他发展出的波动理论是一种振幅表述，主要是用光波的振幅与相位来作分析；振幅表述能够定量地解释偏振光的物理性质；但非偏振光或部分偏振光不具有稳定的振幅与相位，无法用振幅表述给予解释。

1852年，乔治·斯托克斯提出一种强度表述，能够描述偏振光、非偏振光与部分偏振光的物理行为；只需要使用四个参数，后来称为斯托克斯参数（Stokes parameters），就可以描述任何光束的偏振态，更重要地，这四个参数可以直接测量获得。

那时，电磁学理论杂乱无章，詹姆斯·麦克斯韦将这些理论加以整合，于1865年提出麦克斯韦方程组。从这方程组，他推导出电磁波方程，推论出光波是一种电磁波，可以用麦克斯韦方程组作精确描述。菲涅耳的波动理论是建立于一些貌似合理的假定，由于能够正确描述光波的一些物理行为，例如，传播、衍射、偏振等等，符合实验得到的结果，所以才被学术界接受。从麦克斯韦方程组可以严格地推导出菲涅耳的波动理论，给予这理论坚实稳固的基础。

理论概述

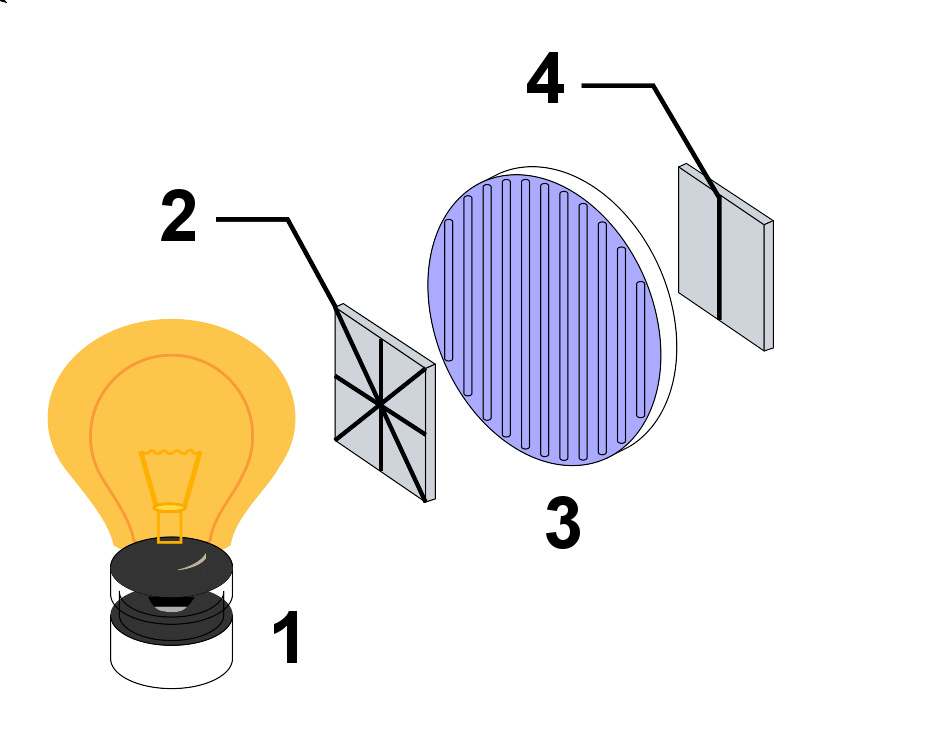
  从白炽灯（1）发射出的非偏振光（2）入射于传输轴为垂直方向的起偏器（3），透射出来的是垂直平面偏振光（4）。

大多数光源属于非偏振光源，例如，太阳、白炽灯等等，因为它们所发射出的光波是由一组不同空间特征、频率（波长）、相位、偏振的光波随机混合所组成。为了了解光波的偏振性质，最简单的方法就是先只思考单色平面波，这种波是具有特定传播方向、频率、相位、振荡方向的正弦波。从研究平面波光学系统的性质与行为，可以对于一般案例给出预测，这是因为任何特定空间结构的光波都可以分解为一组不同频率、不同振幅的平面波，称为其角谱（angular spectrum）。

横电磁波

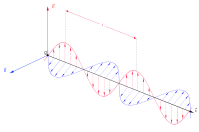
  传播于自由空间的电磁波是横波，电场方向与磁场方向彼此相互垂直，又都垂直于传播方向。

光波是一种电磁波。在自由空间里，电磁波是横波，其电场与磁场的方向都垂直于电磁波的传播方向，并且相互垂直。 设想一个频率为 f {\displaystyle f} 的电磁平面波朝着+z-轴方向传播，电磁波的电场 E ( z , t ) {\displaystyle \mathbf {E} (z,t)} 、磁场 B ( z , t ) {\displaystyle \mathbf {B} (z,t)} 必定平行于xy-平面，以方程表示为

其中， E 0 {\displaystyle \mathbf {E} _{0}} 与 B 0 {\displaystyle \mathbf {B} _{0}} 分别是复常数矢量， k {\displaystyle k} 是波数。

E 0 {\displaystyle \mathbf {E} _{0}} 的x-分量、y-分量分别描述电磁波的电场朝着x方向、y方向的振辐；类似地， B 0 {\displaystyle \mathbf {B} _{0}} 的x-分量、y-分量分别描述电磁波的磁场朝着x方向、y方向的振辐。对于这朝着+z-轴方向传播的横电磁波， E 0 {\displaystyle \mathbf {E} _{0}} 与 B 0 {\displaystyle \mathbf {B} _{0}} 的z-分量都等于0。 B 0 {\displaystyle \mathbf {B} _{0}} 与 E 0 {\displaystyle \mathbf {E} _{0}} 之间的关系为

其中， ϵ ϵ --> 0 {\displaystyle \epsilon _{0}} 为电常数， μ μ --> 0 {\displaystyle \mu _{0}} 为磁常数。

所以，从电磁波的电场可以计算出磁场。

类似地，在简单介质里， B 0 {\displaystyle \mathbf {B} _{0}} 与 E 0 {\displaystyle \mathbf {E} _{0}} 之间的关系为

其中， ϵ ϵ --> {\displaystyle \epsilon } 为电容率， μ μ --> {\displaystyle \mu } 为磁导率。

所以，尽管电磁波传播于简单介质，仍旧可以从电磁波的电场计算出磁场。

由于 E 0 {\displaystyle \mathbf {E} _{0}} 是常数矢量，不会随着时间的流易而改变方向，所以，这电磁波具有偏振性质，偏振方向是 E 0 {\displaystyle \mathbf {E} _{0}} 的方向，偏振平面是 E 0 {\displaystyle \mathbf {E} _{0}} 与z-轴共同组成的平面。由 E 0 {\displaystyle \mathbf {E} _{0}} 的x-分量、y-分量所组成的矢量称为琼斯矢量，可以用来描述偏振。除了给定偏振以外，琼斯矢量还给定了整体电磁波的大小与相位。 特别而言，电磁波的辐照度 I {\displaystyle I} 以方程表示为

其中， η η --> = μ μ --> / ϵ ϵ --> {\displaystyle \eta ={\sqrt {\mu /\epsilon }}} 是这简单介质的特性阻抗（characteristic impedance）

偏振与两个分量的比率有关，在解析偏振问题时，可以约化为只思考 | E 0 x | 2 + | E 0 y | 2 = 1 {\displaystyle |E_{0x}|^{2}+|E_{0y}|^{2}=1} 的电磁波，将电磁波归一化；偏振与两个分量的相对向位有关，因此可以设定 E 0 x {\displaystyle E_{0x}} 的相位为零，换句话说，约化为只思考 E 0 x {\displaystyle E_{0x}} 是实数， E 0 y {\displaystyle E_{0y}} 是复数的偏振问题， E 0 x {\displaystyle E_{0x}} 、 E 0 y {\displaystyle E_{0y}} 分别表示为

其中， Q {\displaystyle Q} 、 ϕ ϕ --> {\displaystyle \phi } 是偏振态的两个参数， − − --> 1 ≤ ≤ --> Q ≤ ≤ --> 1 {\displaystyle -1\leq Q\leq 1} 。

按照常规，当提到偏振时，假若没有特别设定，通常指的是电场的偏振。磁场的偏振通常与电场类似，唯一不同之处是90°空间角度差。

偏振态

线偏振圆偏振椭圆偏振 电场矢量随着时间（z-轴）流易而演变。电场矢量以黑色粗线表示，它的x-分量、y-分量分别以红色细线、蓝色细线表示。在基部的图样是矢量的矢端随着时间流易对于xy-平面的投射。

在正弦波的每一个周期，电场矢量和磁场矢量都会描绘出一个椭圆形（注意到线偏振与圆偏振是椭圆偏振的特别案例）。这椭圆的形状与定向定义了电磁波的偏振态。右图展示出几种不同种类的偏振。假设电场的x-分量、y-分量完全同相，则随着时间流易，电场矢量的矢端对于xy-平面的投射，会描绘出一条直线段，这案例因此称为“线偏振”，又称为“平面偏振”。假设电场的x-分量、y-分量拥有同样的振辐，但是失相90°，则随着时间流易，电场矢量的矢端对于xy-平面的投射，会描绘出一条圆圈，这案例因此称为“圆偏振”。根据光学领域常规，依相位差为-90°或+90°，圆偏振又分为右旋圆偏振（顺时针旋转）或左旋圆偏振（逆时针旋转）。 假设除了失相以外，两个分量的振辐不同，则随着时间流易，电场矢量的矢端对于xy-平面的投射，会描绘出一条椭圆，这案例因此称为“椭圆偏振”。类似地，对应于不同的偏振态，电场的顺时针旋转或逆时针旋转可以制成同样的椭圆形状。

只要光波的传播方向与z-轴同向，而xy-平面的定向可以任意选择，就能够正确地表现每一种偏振态。在解析问题时，通常会选择合适的坐标轴，例如，光波的入射方向与x-轴同平面。另外，任意两个相互正交的偏振态可以设定为基底函数；这样，任意偏振态可以用基底函数来表示，例如，设定两个相互正交的线偏振态为基底函数，则可很自然地处理表面反射、双折射等问题。右旋圆偏振态与左旋圆偏振态也是很有用的选择，可以用来研究光波传播于立体异构的问题。

非偏振光

可见光的大多数常见光源，包括黑体辐射、萤光等，会发射出不相干光波。在这些光源物质里，处于激发态的原子或分子会独立、毫无关联地发射出这些随机偏振的电磁辐射波列。每个波列持续大约10 秒，所以，光波的偏振只能保持不变不超过10 秒。这种光波称为“非偏振光”。这术语所传达出的意思并不精准，因为在任意时刻、任意位置，电场与磁场的方向都很明确，这术语所要传达出的意思为，偏振随时间流易而改变的速度非常快，它不是无法被测量到，就是与实验结果无关。偏振光在通过 消偏器 （ 英语 ： Depolarizer (optics) ） （depolarizer）之后，由于透射光的偏振随时间流易而改变的速率非常快，实际而言，可以忽略透射光在任意时刻的偏振，因此将透射光归类为“非偏振光”。

假若光波的一个偏振模的功率与另一个偏振模的功率不一样，则可称此光波为“部分偏振光”。它可以统计描述为一个完全非偏振光与一个完全偏振光的叠加。 偏振度（degree of polarization）是光波的偏振部分所占有的百分比，可以用来描述光波的成分。部分偏振态最常用斯托克斯参量（Stokes parameters）来设定。

其它种类偏振

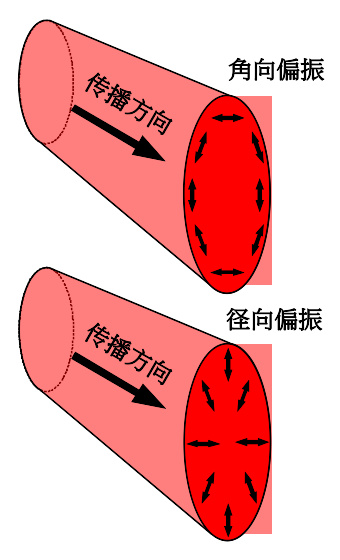
  上图是角向偏振，下图是径向偏振。

除了横波以外，很多种波动的振荡方向不局限为垂直于传播方向。这些案例超过本条目范畴，本条目专注于横波，可是，在有些案例里，相干波的偏振不能简单地用琼斯矢量或斯托克斯矢量描述。

设想先前提到的传播于均匀、各向同性、非衰减性介质的电磁平面波，假设改为传播于各向异性介质，例如双折射晶体，电场或磁场可能还会拥有纵场。对于这种案例，因为介质具有各向异性，它的电极化率或磁导率必需用张量来描述，电场的方向可能不同于电势移的方向，磁场强度的方向可能不同于磁场的方向。 有些各向同性介质的折射率是复数，折射率的很大一部分是虚数，例如，金属。甚至在这些介质里，非均匀波都可以传播；严格而说，它的各个场并不完全是横场。表面波、传播于波导或光纤的电磁波通常不是横波，但是可以以横模（transverse mode）的概念来描述。横模又分为“横电模”、“横磁模”、“横电磁模”、“混合模”四种。

在自由空间里，纵场分量可以被生成于平面波近似不成立的焦区。举一个极端例子，在径向偏振（radial polarization）光或角向偏振（azimuthal polarization）光的焦点，电场与磁场完全是纵场，与传播方向同向。

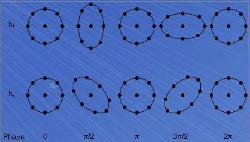
  引力波的十字型偏振h + 与交叉型偏振h × 对于排列成圆圈形状的粒子所产生的振荡效应。

像在流体里传播的声波一类的纵波，振荡方向按照定义是沿着传播方向，所以，偏振这论题通常不会被提出。从另一方面来说，在大块固体传播的声波也可能是横波，也可能是纵波，总共有三个偏振分量。对于这案例，横偏振伴随剪应力的方向，位移方向垂直于传播方向；纵偏振描述固体的压缩与振荡沿着传播方向。在地震学里，横偏振与纵偏振之间的传播差别是很重要的参数。

传递引力的引力子不带质量，具有横向偏振， 因此引力波是横波，引力波的振荡方向垂直于传播方向，具有偏振性质。引力波可以呈两种偏振态，十字型偏振h + 与交叉型偏振h × 。如右图所示，假设一群粒子静止排列成圆圈形状，垂直于这圆圈传播通过的引力波，其h + 偏振会对这些粒子造成可观察到的效应，在某一时刻，它会使得圆圈朝着上下方向拉伸，同时又会朝着左右方向压缩；过一会儿，它又会将这变化逆转回来。类似地，h × 偏振会对这些粒子造成振荡效应。这两种偏振态很相似，将其中一种偏振态旋转45度，就可以得到另一种偏振态。

数学表述

偏振椭圆

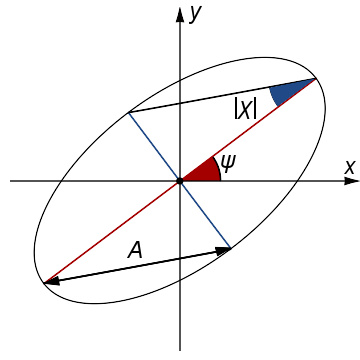
  偏振椭圆图。

“偏振椭圆”可以帮助想像与理解偏振问题。假设横电磁波 E ( z , t ) {\displaystyle \mathbf {E} (z,t)} 的分量为

其中， E 0 x {\displaystyle E_{0x}} 、 E 0 y {\displaystyle E_{0y}} 分别为 E x {\displaystyle E_{x}} 、 E y {\displaystyle E_{y}} 的最大实值。

如右图所示，这个横电磁波的偏振椭圆以方程表示为

其中， φ φ --> = φ φ --> x − − --> φ φ --> y {\displaystyle \varphi =\varphi _{x}-\varphi _{y}} 是相位差。

“椭圆幅” A {\displaystyle A} 估算波动的功率密度，以方程定义为

“定向角” ψ ψ --> {\displaystyle \psi } 定义为偏振椭圆的半长轴与x-轴之间的夹角：

“椭圆角” χ χ --> {\displaystyle \chi } 定义为

偏振椭圆是由椭圆幅、定向角、椭圆角设定。电磁波的偏振方向是由定向角、椭圆角设定。

换另一种写法，定义附属角 α α --> {\displaystyle \alpha } 为

则定向角、椭圆角可以写为

设定 ξ ξ --> ( t ) {\displaystyle \xi (t)} 为电场矢量与x-轴之间的夹角；随着时间流易，电场矢量的矢端会沿着椭圆旋转，从+z-坐标位置朝原点看，假若呈逆时针旋转，则 ξ ξ --> ( t ) {\displaystyle \xi (t)} 正在单调递增，电磁波是左旋椭圆偏振；假若呈顺时针旋转，则 ξ ξ --> ( t ) {\displaystyle \xi (t)} 正在单调递减，电磁波是右旋椭圆偏振。所以，从 ξ ξ --> ( t ) {\displaystyle \xi (t)} 对于时间 t {\displaystyle t} 的导数，可以推断出电磁波是哪一种偏振；假若导数大于零，则电磁波是左旋椭圆偏振；假若导数小于零，电磁波是右旋椭圆偏振。在任意固定位置 z 0 {\displaystyle z_{0}} ，判断角 ξ ξ --> ( t ) {\displaystyle \xi (t)} 以方程表示为

导数与相位差 φ φ --> {\displaystyle \varphi } 之间的关系为

所以，假若相位差 0 ≤ ≤ --> π π --> {\displaystyle 0 ，则椭圆角 0 ≤ ≤ --> π π --> / 4 {\displaystyle 0 ，电磁波是右旋椭圆偏振；假若相位差 − − --> π π --> ≤ ≤ --> φ φ --> < 0 {\displaystyle -\pi \leq \varphi π π --> / 4 ≤ ≤ --> χ χ --> < 0 {\displaystyle -\pi /4\leq \chi <0} ，电磁波是左旋椭圆偏振。

在十九世纪，偏振椭圆是唯一能帮助想像与理解偏振问题的方法。但是，这方法有个缺点，假若光束必须传播通过很多偏振器材，描述偏振行为的方程会变得很烦杂，很难找到解答。一直等到1892年，昂利·庞加莱提出庞加莱球（Poincaré sphere）后，才有了更好的解析方法。

琼斯矢量与琼斯矩阵

琼斯矢量可以用来描述完全偏振光；它不能用来描述非偏振光与部分偏振光。假设横电磁波 E ( z , t ) {\displaystyle \mathbf {E} (z,t)} 的分量为

其中， E 0 x {\displaystyle E_{0x}} 、 E 0 y {\displaystyle E_{0y}} 分别为 E x {\displaystyle E_{x}} 、 E y {\displaystyle E_{y}} 的最大实值。

这横电磁波的琼斯矢量 J {\displaystyle \mathbf {J} } 为

通常，琼斯矢量会被归一化成为单位矢量。通过归一化后，几个常用的琼斯矢量可以很容易地被辨认出来。例如，平行于x-轴的线偏振（水平偏振）、平行于y-轴的线偏振（垂直偏振），它们的琼斯矢量 J h {\displaystyle \mathbf {J} _{h}} 、 J v {\displaystyle \mathbf {J} _{v}} 分别为

左旋圆偏振、右旋圆偏振的琼斯矢量 J L {\displaystyle \mathbf {J} _{L}} 、 J R {\displaystyle \mathbf {J} _{R}} 分别为

两个偏振态 E 1 {\displaystyle \mathbf {E} _{1}} 、 E 2 {\displaystyle \mathbf {E} _{2}} 相互正交，当且仅当分别代表它们的两个琼斯矢量 J 1 {\displaystyle \mathbf {J} _{1}} 、 J 2 {\displaystyle \mathbf {J} _{2}} 相互正交，以方程表示，

因此，水平偏振态与垂直偏振态相互正交，因为 J h {\displaystyle \mathbf {J} _{h}} 与 J v {\displaystyle \mathbf {J} _{v}} 相互正交：

左旋圆偏振态与右旋圆偏振态相互正交，因为 J L {\displaystyle \mathbf {J} _{L}} 与 J R {\displaystyle \mathbf {J} _{R}} 相互正交：

这些相互正交的琼斯矢量对形成一个基底，可以用来表示任意琼斯矢量。例如， J L {\displaystyle \mathbf {J} _{L}} 与 J R {\displaystyle \mathbf {J} _{R}} 可以用来表示任意完全偏振态的琼斯矢量；在双折射介质里，左旋圆偏振态与右旋圆偏振态各自具有不同的物理行为，这可以分别用这两个琼斯矢量来代表与作估算。

琼斯矩阵是作用于琼斯矢量的算符。在实际实验里，琼斯矩阵是由各种光学元件实现，例如，透镜、分光器、镜子等等。举个简单例子，水平线性偏振片、垂直线性偏振片的琼斯矩阵分别为

给定入射光为左旋圆偏振光 J L {\displaystyle \mathbf {J} _{L}} ，光学元件为水平线性偏振片 M h {\displaystyle \mathbb {M} _{h}} ，那么，透射光为水平偏振光，其琼斯矢量为

斯托克斯参数与穆勒矩阵

非偏振光与部分偏振光不能用琼斯矢量来描述，必需使用斯托克斯参数才能正确描述。斯托克斯参数 S 0 {\displaystyle S_{0}} 、 S 1 {\displaystyle S_{1}} 、 S 2 {\displaystyle S_{2}} 、 S 3 {\displaystyle S_{3}} 是可以用仪器测量到的物理量，假设 I 0 {\displaystyle I_{0}} 、 I 1 {\displaystyle I_{1}} 、 I 2 {\displaystyle I_{2}} 、 I 3 {\displaystyle I_{3}} 分别是光束的总体、水平偏振部分、 + 45 ∘ ∘ --> {\displaystyle +45^{\circ }} 偏振部分、右旋圆偏振部分的辐照度，斯托克斯参数操作定义为

只要测量光束的 I 0 {\displaystyle I_{0}} 、 I 1 {\displaystyle I_{1}} 、 I 2 {\displaystyle I_{2}} 、 I 3 {\displaystyle I_{3}} ，就可简单估算出斯托克斯参数。

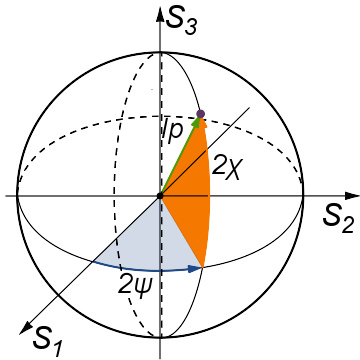
  庞加莱球图。 I p = I 0 P {\displaystyle I_{p}=I_{0}{\mathcal {P}}} 。

为了便利运算，将斯托克斯参数组成一个矢量，称为“斯托克斯矢量”。 斯托克斯参数与辐照度、偏振度 P {\displaystyle {\mathcal {P}}} 、偏振椭圆参数之间的关系为

对于偏振光， P = 1 {\displaystyle {\mathcal {P}}=1} ，所以，

对于非偏振光， P = 0 {\displaystyle {\mathcal {P}}=0} ， I 0 = I 1 = I 2 = I 3 {\displaystyle I_{0}=I_{1}=I_{2}=I_{3}} ，所以，斯托克斯矢量为

部分偏振光是偏振光与非偏振光的权重组合：

部分偏振光的偏振度 P {\displaystyle {\mathcal {P}}} 为

通常，整个斯托克斯矢量会被除以 S 0 {\displaystyle S_{0}} ，这意味着光束具有单位辐照度。例如，水平偏振光、垂直偏振光的斯托克斯矢量分别为

光学元件作用于光束的效应必须用 穆勒矩阵 （ 英语 ： Mueller matrix ） 估算。一般而言，每一种实际光学元件都有其对应的穆勒矩阵，这是琼斯矩阵的延伸至非偏振光与部分偏振光论题。穆勒矩阵是一个4×4实值矩阵。 例如，水平线性偏振片、垂直线性偏振片的琼斯矩阵分别为

给定入射光的斯托克斯矢量 S {\displaystyle \mathbf {S} } 、光学元件的穆勒矩阵 M {\displaystyle \mathbb {M} } ，就可以算出透射光的斯托克斯矢量 S ′ {\displaystyle \mathbf {S} "} ：

例如，假设入射光为非偏振光 S n {\displaystyle \mathbf {S} _{n}} ，光学元件为水平线性偏振片 M h {\displaystyle \mathbb {M} _{h}} ，那么，透射光为水平偏振光，其斯托克斯矢量为

更进阶的矩阵方法涉及到相干矩阵（coherency matrix）的表述。

偏振测量技术

测量应力

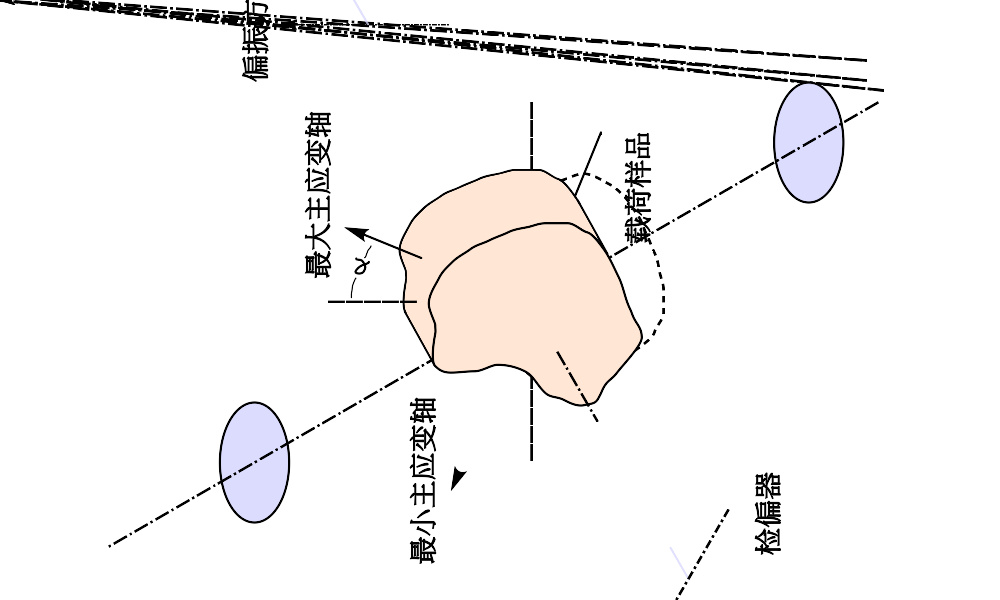
  平面偏光仪工作示意图。

  使用偏光仪，可以观察到塑胶玻璃感受到的应力。

假若两块不同类型的偏振片分别制成的两种偏振光相互正交，则称它们为“正交偏振片”。例如，水平偏振片与垂直偏振片分别制成的水平偏振光与垂直偏振光相互正交，它们是两块正交偏振片。类似地，左旋圆偏振片与右旋圆偏振片也是两块正交偏振片。这实验设置简单地组成偏光仪（polariscope），又称“偏振光镜”；光束最先入射的偏振片为起偏器，然后再入射的偏振片为检偏器；水平偏振片与垂直偏振片共同组成“平面偏光仪”；左旋圆偏振片与右旋圆偏振片共同组成“圆偏光仪”。如右图所示，假设照射光束于由水平偏振片制成的起偏器，因为透射过的水平偏振光会被由垂直偏振片制成的检偏器吸收，不能透射过垂直偏振片；所以，光束无法通过两块正交偏振片共同组成的偏光仪，透射的幅照度为零。但是假设将双折射物质置入偏光仪内，即两块正交偏振片之间，光束在通过双折射物质的过程中，偏振会被旋转，因此可以从偏光仪观察到透射光的色彩图样，并且测量到其幅照度。

各向同性固体不会显示出双折射现象。但是，假设施加机械应力，则会发生双折射现象。制造塑胶成品的注射成型过程可能会将所施加的机械应力冷冻在塑胶成品里。偏光仪可以用来分析双折射物质所感受到的应力与应变。将双折射物质置入偏光仪内，从测量到在任意位置的透射幅照度，可以估算在双折射物质对应位置所感受到的应力与应变。光弹性法（photoelasticity）应用这偏振理论来分析固体所感受到的机械应力。这是一种极具功能的实验方法，在结构工程学与机械工程学有广泛的用途。

椭圆偏振测量术

椭圆偏振测量术是一种用途极广的技术，可用来测量均匀表面的光学性质；简略描述其程序，就是在均匀表面做镜面反射后，测量光波的偏振态的改变；通常这函数的参数为入射角与波长。由于椭圆偏振测量术倚赖反射机制，样品不需要具有透明性质，探测仪器也不需要从样品背部测量透射光的辐照度，这技术还可以应用于吸光度极高的物质，并且不具有破坏性，只需要很少量的样品就可以做测量。

椭圆偏振测量术也可以用来测量薄膜的复折射率与厚度。应用椭圆偏振技术，照射光束于薄膜样品，然后分析反射光的偏振改变，即可估算复数折射率或介电函数张量，以此获得基本的物理参数，这包括表面粗糙度（roughness）、晶体质量、化学成分或导电性。它常被用来鉴定单层或多层堆叠的薄膜厚度，可量测厚度由数Å到几微米，甚至小至一个单原子层，并且准确性极高。

地质学

 火山沙粒的显微照片；上图使用的是平面偏振光，下图是偏光仪。在中间靠左位置的尺寸块宽度为0.25 mm。

很多晶体矿石具有线性双折射性质，这促成了偏振现象的初始发现。在矿物学里，偏振显微镜时常会应用这双折射性质来辨识矿石。更详尽说明，请参阅光学矿物学（optical mineralogy）。

地震学

在地震学里，地震波主要分为两种，一种是面波，一种是体波。面波传播于地球表面，体波传播于地球内部。体波又分成纵波和横波两种：

纵波在这里被称为P波，P代表主要（primary）或压强（pressure），纵波是一种压缩波，粒子振动方向平行于地震波的前进方向，在所有地震波中，它的前进速度最快，也最早抵达地表。P波能传播于固体、液体或气体。

横波在这里被称为S波，S意指次要（secondary）或剪切力（shear），横波是一种剪切波（shear wave），粒子振动方向垂直于地震波的前进方向，它的前进速度仅次于P波。S波只能在固体中传播，由于地球外核呈液态，S波无法穿过外核。

由于P波和S波的传播速度不同，利用两者之间的走时差，可作简单的地震定位。

化学

根据平面偏振光通过由手性物质时偏振平面旋转的方向，可以将手性物质的对映异构体分类为左旋、右旋两种；朝着光源望去，左旋对映异构体会使得偏振平面朝着逆时针方向旋转，右旋对映异构体会使得偏振平面朝着顺时针方向旋转。这种偏振平面被旋转的现象，称为“圆双折射现象”，能够造成这种现象的物质称为光学活性物质。由于这两种手性物质里的每一个化学键的性质与能量都相同，两种物质的沸点、熔点、密度等等都一样，应用圆双折射现象，可以辨识手性物质的种类到底是左旋还是右旋。

假若在样品溶液内，左旋与右旋对映异构体的数量相等（称这种样品为外消旋混合物），则它们各自产生的效应会相互抵销，不会产生圆双折射现象；假若只有一种对映异构体，或者其中某种对映异构体数量较多，则会出现圆双折射现象（或旋光性，光学活性），从而显示出不平衡程度的大小（或者物质的浓度，假若只有一种对映异构体存在）。偏振计可以用来量度这种现象。偏振计里面有一个起偏器与一个检偏器。将起偏器制成的偏振光入射于光学活性液体，使偏振光被旋转有限角度，调整检偏器的旋转角度，当透射过检偏器的光强变得最大之时，检偏器的旋转角度可以用来估算光学活性液体所造成的旋转角度。液体样品的旋光率（specific rotation）等于旋转角度除以样品长度。

天文学

恒星分光偏振谱仪（stellar spectropolarimeter）可以用来测量恒星的磁场，这种仪器是摄谱仪和偏振计的结合。第一个来研究恒星磁场的仪器命名为“NARVAL”，被安装在法国比利牛斯山比格尔地区的贝尔纳·李奥望远镜上 。

虽然关于恒星热辐射的研究通常不会涉及到偏振，很多相干性天文辐射源会发射出偏振辐射，例如羟基微波激射、甲醇微波激射等等天体微波激射（astrophysical maser），另外，星际尘埃也会借着散射机制将星光偏振化。对于这些偏振辐射做偏振测量可以给出关于辐射源、辐射源附近恒星形成的区域关于磁场的信息。 由于地球与太阳的磁场超强于星际磁场，普通方法无法直接地测量到星际磁场；必需使用特别方法，例如，可以应用法拉第效应来测量星际磁场。从遥远辐射源发射出的偏振射电辐射，其偏振平面因法拉第效应产生的旋转角度与磁场成正比。使用这种方法测量到星际磁场大约为10 -10 T。

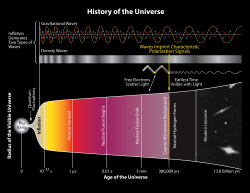
宇宙微波背景的偏振可以用来研究宇宙暴胀的各种物理行为，特别是宇宙暴胀产生的引力辐射与能量尺寸(10 –10 GeV) 。 这是普朗克卫星的重要任务之一。

天文学者认为，天文辐射很可能促成了地球生物分子的手性。

重要应用

偏光太阳镜

  起偏器对于从淤泥滩的反射光所产生的效应：左图显示出，偏振轴与水平线平行的起偏器会透射这些反射光；右图显示出，旋转这起偏器90°会阻挡几乎全部镜面反射光，如同使用偏光太阳镜。

照射非偏振光于镜面表面（光亮表面），通常得到的反射光会具有某种程度的偏振。1808年，法国物理学者艾蒂安-路易·马吕斯最先观察到这现象。偏光太阳镜利用这效应来降低水平表面反射出来的眩光，特别是当太阳从前方斜照下来时，张眼往前方路面望去会看到的强劲眩光。

天空中的偏振光

  右边照片显示出偏振滤光片对于天空景色产生的效应。

传播于地球大气层的太阳光会因为被大气分子瑞利散射而使得散射光产生偏振，从天空中的散射光可以观察到这现象。散射光在清晰的天空中会显得更明亮、更具色彩。在天空中，与太阳照射的光束呈直角方向的位置，最容易观察到这偏振现象（偏振方向与太阳光方向、直角方向相垂直）。这种具有部分偏振的散射光，假若使用起偏器，可以使得照片里的天空变得较黑，增加衬度（contrast）；这样，可以改良照片的品质。

出现在天空中的偏振光常被用来导航定向。从九世纪至十一世纪间，维京人时常航行于北大西洋。那时期，欧洲人尚未知道怎样使用磁罗盘，维京人主要是使用太阳与星星来导航定向，可是，在阴天，这方法无效。学者猜测他们可能知道怎样使用一种称为“太阳石”（sunstone）的简单仪器，但这争议性理论尚未被证实。1950年代，运输飞机航行在地磁极附近时，由于无法使用磁罗盘，假若无法看到太阳或星星时（例如，在阴天或黄昏），时常会使用“天空罗盘”（sky compass）来导航。这仪器是一种很精致的偏光仪，可以用来观测天空中的偏振光。十九世纪后期， 查理斯·惠斯通（Charles Wheatstone）发明了偏振钟（polar clock）。这也是一种偏光仪，可以用来计时。根据惠斯通，偏振钟比日晷的优点更多。

液晶显示器

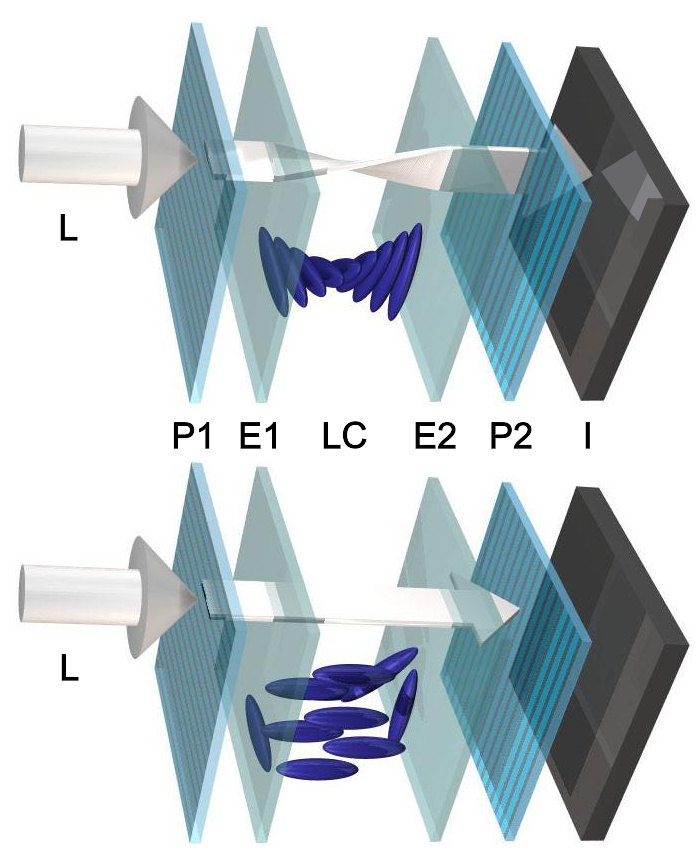
  上方：电路断开，液晶亮。 下方：回路接通，液晶不亮。

液晶显示器（LCD）科技倚赖液晶来旋转偏振光的偏振平面。如右图所示，在两块正交平面偏振片P1、P2之间置入透明电极层E1、E2和扭曲向列型液晶LC。照射非偏振光L于偏振片P1，透射光会呈平面偏振。

上方图：当E1、E2不通电时，液晶分子会呈螺旋状排列，平面偏振光的偏振平面会被液晶LC逐渐扭曲，因此平面偏振光才能透射过正交的偏振片P2。假设安装镜子I，则透射过的平面偏振光会被反射回来（注意到显示于镜子的反射光箭头），其偏振平面会再被液晶朝反方向扭曲，因此才能透射过正交的偏振片P1。从初始发光源位置朝着偏振片P1望去，会观察到明亮的反射光。

下方图：当电极E1、E2通电时，液晶分子会顺着电场方向排列，因此液晶不会扭曲平面偏振光的偏振平面，由于两块偏振片的偏振轴相互垂直，这时光线不能透射过偏振片P2。虽然安装镜子I，从原先发光源位置朝着平面偏振片P1望去，仍旧不会观察到任何反射光。

应用这机制，液晶显示器能够显示简单的文字或图案信息，它的主要优点是功耗较低，因此可以使用光电池来供电。

三维电影

三维电影所使用的立体显示技术将两个不同影像分别传输至左眼、右眼。现今，这技术的首选方法是“偏振编码”；使用两台投影机将两个不同影像都投射到投影屏，每一台投影机都安装了偏振轴相互垂直的起偏器；或者使用单台能够时分复用偏振的投影机（内部安装了快速过滤交替偏振的元件）。三维眼镜的左边镜片与右边镜片分别具有对应的检偏器，确使每一只眼睛只会接收到对应的偏振影像。早先，采用平面偏振编码，因为费用较便宜、分离效果很好。但是，圆偏振所形成的分离影像不会受到观众头部倾斜的影响。现今，三维电影已广泛采用圆偏振技术，例如RealD 戏院系统。圆偏振技术需要使用特殊的投影屏，例如“银屏”（silver screen），这种投影屏能够维持投射影像的圆偏振，不会在反射时被非偏振化；普通的白色漫反射投影屏会造成投射影像在反射时被非偏振化，无法用来展示三维电影。

动物视觉

很多种动物可以感视到偏振光的光强与方向。通常它们会用这能力来导航。很多种昆虫也具有这种辨识偏振光的能力，包括蜜蜂在内，蜜蜂用来表达食物源方向的舞蹈就是用这信息来定向。 生物学者经过仔细研究发觉，章鱼、鱿鱼、乌贼、虾蛄可以感视到偏振光。生物学者猜想，章鱼、鱿鱼、乌贼使用这能力来探测会反射光的鱼。有些鱼会用反射光机制来掩饰自己。但是反射光的偏振与海水的散射偏振不同，因此鱼的这种掩饰可以被破解。乌贼的快速变化、鲜艳颜色、具有偏振功能的表皮图案，可以用来彼此传达信息。 某种虾蛄能够观察偏振的所有六个正交分量（水平、垂直、对角、反对角、左旋圆、右旋圆），被认为具有最优化的偏振视觉。 信鸽被认为能够感视到天空的偏振光，这种能力可以帮助它们远距离归巢。但是，严格做实验检验证实这纯属谣传。

假若不藉用任何滤光器，则人的肉眼对于偏振光的视觉非常微弱。偏振光会在视场中心附近造成很模糊的图样，称为海丁格刷（Haidinger"s brush）。这种图样非常难看到，但若经过一番练习，人可以用他的肉眼观察到偏振光。

圆偏振的角动量

电磁辐射朝着传播方向带有线性动量。另外，圆偏振光还带有角动量。与动量相比，这角动量非常小，很难测得。可是，在一个很值得注意的实验里，应用这性质，达成了令人难以想像的高旋转速度。

英国圣安德鲁斯大学实验团队使得一个直径4微米的微观尺度碳酸钙圆球以每分钟6亿圈速度旋转。应用光镊技术，这个圆球被圆偏振激光束悬浮起来。由于碳酸钙圆球具有双折射性质，透射光的偏振度（degree of polarization）会被降低，因此失去一些角动量给圆球。被悬浮于几乎真空，遭受到微乎其微的摩擦力，圆球的旋转速度可以增加至每分钟6亿圈。这旋转速度对应于离心加速度大约为地球表面引力的10亿倍，但是令人惊奇的是，圆球并没有因此被击碎。

参见

消偏器 （ 英语 ： Depolarizer (optics) ）

径向偏振 （ 英语 ： Radial polarization ）

偏振片

克尔效应

泡克耳斯效应

偏振光显微镜 （ 英语 ： Polarized light microscopy ）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。