力的平衡

合力的定义表明，任意数目的力作用在一个物体上，它们的总作用，可用它们的合力代替。

在生活中，人们经常发现，物体即使在受到外力作用时也能保持静止或匀速直线运动状态，这似乎与牛顿第一定律相矛盾。可以运用合力来解释这一问题。因为，当几个力的合力使物体保持静止或匀速直线状态的时候。这几个力互称为平衡力。这个时候各个分力的作用效果互相抵消，从效果上来看，物体此时不受力。这样，就不于牛顿第一定律相矛盾了。

力的合成

求已知几个力的合力，称为力的合成。

作用于同一点上的力叫做共点力，以下讨论，都只在共点力的基础上进行。

平行四边形法则

平行四边形法则适用于两个互成角度的共点力上，可以通过以下实验证明：

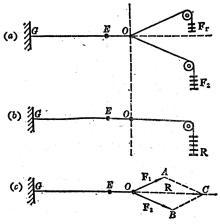
如图（a）、（b)橡皮带GE在力F1{\displaystyle F_{1}}和F2{\displaystyle F_{2}}的共同作用下伸长了OE，在力R{\displaystyle R}的作用下，也伸长了OE。它们的作用效果相同，所以F1{\displaystyle F_{1}}、F2{\displaystyle F_{2}}的合力为R{\displaystyle R}。在力F1{\displaystyle F_{1}}、F2{\displaystyle F_{2}}和R{\displaystyle R}的方向上各做有向线段，并以一定的标度使OA→ → -->{\displaystyle {\vec {OA}}}、OB→ → -->{\displaystyle {\vec {OB}}}、OC→ → -->{\displaystyle {\vec {OC}}}的长度分别表示这三个力的大小。连接AC{\displaystyle AC}和BC{\displaystyle BC}，可以证明四边形OABC是平行四边形，OC是它的对角线。

经过大量实验证明，两个互成角度的共点力，它们的合力的大小和方向，可以用表示这两个力的有向线段做邻边做画出的平行四边形的对角线来表示，这就是平行四边形法则。

两个以上的共点力合成时，也可以应用平行四边形法则求它们的合力。方法是先求出任意两个力的合力，再求出这个合力与第三个力的合力，这样继续下去，最后得出的就是这几个多力的合力。

根据平行四边形法则，在其他因素不改变的情况下，合力的大小与二力的夹角成反比。

力的合成的计算

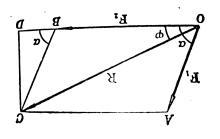
根据平行四边形法则，可以计算合力的具体大小和方向。

在△ △ -->OBC{\displaystyle \bigtriangleup OBC}中，通过余弦定理，可得：

OC2=BC2+OB2− − -->2BC⋅ ⋅ -->OBcos⁡ ⁡ -->(180∘ ∘ -->− − -->α α -->){\displaystyle OC^{2}=BC^{2}+OB^{2}-2BC\cdot OB\cos {\bigl (}180^{\circ }-\alpha {\bigr )}}

∵ ∵ -->BC=F1,OB=F2,OC=R{\displaystyle \because BC=F_{1},OB=F_{2},OC=R}

∴ ∴ -->R2=F12+F22− − -->2F2F2cos⁡ ⁡ -->(180∘ ∘ -->− − -->α α -->){\displaystyle \therefore R^{2}=F_{1}^{2}+F_{2}^{2}-2F_{2}F_{2}\cos {\bigl (}180^{\circ }-\alpha {\bigr )}}

∴ ∴ -->R=F12+F22+2F1F2cos⁡ ⁡ -->a{\displaystyle \therefore R={\sqrt {F_{1}^{2}+F_{2}^{2}+2F_{1}F_{2}\cos a}}}

合力的方向可以用力R{\displaystyle R}跟F2{\displaystyle F_{2}}的夹角φ φ -->{\displaystyle \varphi }表示出来。由Rt△ △ -->ODC{\displaystyle Rt\vartriangle ODC}可以求φ φ -->{\displaystyle \varphi }的大小

tan⁡ ⁡ -->φ φ -->=CDOD=CDOB+BD=Fin⁡ ⁡ -->α α -->F2+F1cos⁡ ⁡ -->α α -->{\displaystyle \tan \varphi ={\frac {CD}{OD}}={\frac {CD}{OB+BD}}={\frac {F_{1}\sin \alpha }{F_{2}+F_{1}\cos \alpha }}}

以上两式，就是计算合力的大小与方向的公式。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。