原理

滴定过程需要一个定量进行的反应，此反应必须能完全进行，且速率要快，也就是平衡常数、速率常数都要较大。而且反应中干扰测量的副产物以及副反应的程度都必须降到误差允许的范围以内，在常量分析的范畴中，这个限度通常是±0.1％。

在两种溶液的滴定中，通常装在滴定管中的溶液称作 滴定剂 （ titrant ），是已知浓度的溶液，即是 标准溶液 （ standard solution ），而未知浓度的溶液则装在下方的锥形瓶里。标准溶液的浓度是与不易变质的固体 标准试剂 （ primary standard ）滴定而测得的。

滴定结束时，读出用去滴定管中溶液的体积，即可用公式算出浓度。

根据反应类型的不同，滴定分为以下种类：

酸碱中和滴定（利用中和反应）

氧化还原滴定（利用氧化还原反应）

沉淀滴定（利用生成沉淀的反应）

络合滴定（利用络合反应）

指示剂

滴定反应需要灵敏的指示剂来指示反应的完成。指示剂在反应完成时，会迅速变成另一种颜色，这样实验者就可以根据指示剂的变色来确定反应的终止。这两个变化通常不是同时完成的，反应定量完成时的状态叫 计量点 （ stoichiometric point ）或 当量点 （ equivalence point ），指示剂变色时的状态叫 滴定终点 （ end point ）。然而通过选用恰当的指示剂可以将指示剂带来的误差（称作 终点误差 ， end point error ）降到允许范围之内。

指示剂一般有两种形态，两种形态呈现不同的颜色。有的指示剂有三种不同颜色的形态。指示剂在滴定终点前后，在两种颜色之间发生颜色渐变的范围叫做 变色范围 。指示剂在变色范围内呈现过渡色。

中和滴定的指示剂是有机弱酸或弱碱，它们的变色范围在等电点附近。如弱酸的变色（以HIn代表）：

HIn (酸色形) = H + In (碱色形)

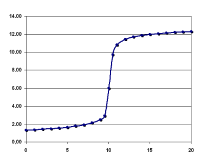
  NaOH滴入HCl的滴定曲线，在pH=7附近发生突跃。横轴是NaOH体积，纵轴是pH值。

由于在变色范围时会发生“突跃”现象，颜色会变得很迅速，只要1滴溶液就可以让指示剂完全变色，因此选择指示剂时，只需让反应完成时的pH值落在突跃范围内即可满足误差要求，不必再苛求准确。

其他种类滴定的指示剂一般是与某种反应物有灵敏反应的物质。络合滴定的指示剂对金属离子的浓度敏感，计量点前后金属离子的浓度发生突跃，可选用终点落在此范围内的指示剂。沉淀滴定的指示剂与金属离子形成沉淀或有色物质，当溶液中被测组分沉淀完全后，金属离子即与指示剂反应发生变色。氧化还原滴定的指示剂是氧化剂或还原剂，在滴定终点时溶液的电势会将其还原（或氧化），从而变色。

有些反应物自身就可以作为指示剂，如高锰酸钾。

操作

滴定操作需要用到一种专门的仪器：“滴定管”。滴定管很细，因此读数也较精确，最小刻度为0.1mL，读数还要估读一位（0.01mL）。

由于滴定要求极准确，所以滴定管及其下方的锥形瓶都要求清洁，在滴定前（若不确保干净）都要用肥皂水洗一遍，再用自来水、蒸馏水各洗2～3遍。由于滴定管是量具，有浓度要求，所以之后还要润洗滴定管，用待装溶液润洗2～3遍。出于节约，、润洗都秉着少量多次的原则。

酸式滴定管能用于酸性，中性，和强氧化性试剂的量取，但不可以装填碱性试剂;碱式滴定管可以用于碱性，中性溶液的量取，但不可以装填酸性和强氧化性试剂（否则会腐蚀橡胶开关）．

滴定之前，先检查滴定管。先将滴定管装满水，竖直放置，检查是否漏液。润洗之后要装上溶液并打开活塞放液，赶尽管的空气泡。滴定之前要读一次数，因此放液之后要把液面调至某个整数刻度（通常是0刻度）以便读数。

在锥形瓶被滴溶液中滴入几滴指示剂。按照实验规程，滴定管中的液体要逐滴滴下，每滴一滴都要摇荡锥形瓶。然而在实际操作中，熟练的实验员可以先很快地放液，在接近变色点时放慢速度，改为逐滴滴下，这样节省不少时间。

当指示剂变色时，停止放液，震荡30秒后，若颜色不褪去，读出滴定管读数。前后两个读数相减即为用去溶液体积。

通常进行滴定实验至少要进行两次，取平均值，两次所用标准溶液体积相差不能超过0.02ml,再取平均值，以确保准确。

仪器分析中的滴定

在没有合适的指示剂可用的情况下，通过仪器分析的方法来判定滴定反应的计量点是一种较好的途径。

电位滴定

电位滴定 利用溶液电势与滴入滴定剂体积的关系判定反应的计量点。计量点前后，溶液电势发生突跃，通过随时测量滴定剂的体积和溶液电势，即可找出该点。

所用的测量装置包括一个电压计，连接一个参比电极（电势不变）和一个指示电极。指示电极内外离子浓度不同导致电势差( E )，这个电势差与待测离子浓度的对数成线性关系。pH计就是依据这个原理制成的。

为了提高测量精度，可以改用 Δ Δ --> E Δ Δ --> V {\displaystyle {\frac {\Delta E}{\Delta V}}} 对 V （滴定剂体积）作图，视“导数”的最高点为滴定终点。也可以用 Δ Δ --> 2 E Δ Δ --> V 2 {\displaystyle {\frac {\Delta ^{2}E}{\Delta V^{2}}}} 对 V 作图，视“二阶导数”的变号之处为滴定终点。需要说明，由于测量是散点式的，这些量并不是真正的导数、而是差分。实际应用时，假定每两个测量点之间的变化幅度是线性的。

参看

分析化学

定量分析

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。