置换的数算

此节使用置换的传统定义。从 n {\displaystyle n} 个相异元素中取出 k {\displaystyle k} 个元素， k {\displaystyle k} 个元素的排列数量为：

其中P意为Permutation（排列），!表示阶乘运算。

以赛马为例，有8匹马参加比赛，玩家需要在彩票上填入前三胜出的马匹的号码，从8匹马中取出3匹马来排前3名，排列数量为：

因为一共存在336种可能性，因此玩家在一次填入中中奖的概率应该是：

不过，教科书则是把从n取k的情况记作 P n k {\displaystyle P_{n}^{k}} 或 A n k {\displaystyle A_{n}^{k}} （A代表Arrangement，即排列）。

重复置换

上面的例子是建立在取出元素不重复出现状况。

从 n {\displaystyle n} 个元素中取出 k {\displaystyle k} 个元素， k {\displaystyle k} 个元素可以重复出现，这排列数量为：

以四星彩为例，10个数字取4个数字，因可能重复所以排列数量为：

这时的一次性添入中奖的概率就应该是：

抽象代数

在集合论与抽象代数等领域中，“置换”一词被保留为集合（通常是有限集）到自身的双射的一个称呼。例如对于从一到十的数字构成的集合，其置换将是从集合 { 1 , … … --> , 10 } {\displaystyle \{1,\ldots ,10\}} 到自身的双射。一个集合上的置换在函数合成运算下构成一个群，称为对称群或置换群。

符号

更多资料：对称群

以下仅考虑有限集上的置换（视为双射），由于 n {\displaystyle n} 个元素的有限集可以一一对应到集合 { 1 , … … --> , n } {\displaystyle \{1,\ldots ,n\}} ，有限集的置换可以化约到形如 {1, ..., n} 的集合之置换。此时有两种表示法。

第一，利用矩阵符号将自然排序写在第一列，而将置换后的排序写在第二列。例如：

表示集合 {1,2,3,4,5} 上的置换 s : s ( 1 ) = 2 , s ( 2 ) = 5 , s ( 3 ) = 4 , s ( 4 ) = 3 , s ( 5 ) = 1 {\displaystyle s:s(1)=2,s(2)=5,s(3)=4,s(4)=3,s(5)=1} 。

第二，借由置换的相继作用描述，这被称为“轮换分解”。分解方式如下：固定置换 s {\displaystyle s} 。对任一元素 x {\displaystyle x} ，由于集合有限而 s {\displaystyle s} 是双射，必存在正整数 N {\displaystyle N} 使得 s N ( x ) = x {\displaystyle s^{N}(x)=x} ，故可将置换 s {\displaystyle s} 对 x {\displaystyle x} 的相继作用表成 ( x s ( x ) s 2 ( x ) ⋯ ⋯ --> s m − − --> 1 ( x ) ) {\displaystyle (x\;s(x)\;s^{2}(x)\cdots s^{m-1}(x))} ，其中 m {\displaystyle m} 是满足 s m ( x ) = x {\displaystyle s^{m}(x)=x} 的最小正整数。

称上述表法为 x {\displaystyle x} 在 s {\displaystyle s} 下的轮换， m {\displaystyle m} 称为轮换的长度。我们在此将轮换视作环状排列，例如

是同一个轮换。由此可知 x {\displaystyle x} 在 s {\displaystyle s} 下的轮换只决定于 x {\displaystyle x} 在 s {\displaystyle s} 作用下的轨道，于是，任两个元素 x , y {\displaystyle x,y} 或给出同一个轮换，或给出不交的轮换。

我们将轮换 ( x 1 ⋯ ⋯ --> x m ) {\displaystyle (x_{1}\;\cdots x_{m})} 理解为一类特殊的置换：仅须定义置换 s {\displaystyle s} 为 s : x 1 ↦ ↦ --> x 2 , … … --> , x m − − --> 1 ↦ ↦ --> x m , x m ↦ ↦ --> x 1 {\displaystyle s:x_{1}\mapsto x_{2},\ldots ,x_{m-1}\mapsto x_{m},x_{m}\mapsto x_{1}} ，而在其它元素上定义为恒等映射。不交的轮换在函数合成的意义下可相交换。

因此我们可以将集合 {1, ..., n} 对一置换分解成不交轮换的合成，此分解若不计顺序则是唯一的。例如前一个例子的 s {\displaystyle s} 就对应到 (1 2 5) (3 4) 或 (3 4) (1 2 5)。

特殊置换

在上节的轮换表法中，长度等于二的轮换称为换位，这种轮换 ( x y ) {\displaystyle (x\;y)} 不外是将元素 x , y {\displaystyle x,y} 交换，并保持其它元素不变。对称群可以由换位生成。

轮换长度为偶数之轮换称为偶轮换，反之则为奇轮换；由此可定义任一置换的奇偶性，并可证明：一个置换是偶置换的充要条件是它可以由偶数个换位生成。偶轮换在置换群中构成一个正规子群，称为交错群。

计算理论中的置换

某些旧课本将置换视为变数值的赋值。在计算机科学中，这就是将值

赋予变数

的赋值运算子，并要求每个值只能赋予一个变数。

赋值/代入的差别表明函数式编程与指令式编程之差异。纯粹的函数式编程并不提供赋值机制。现今数学的惯例是将置换看作函数，其间运算看作函数合成，函数式编程也类似。就赋值语言的观点，一个代入是将给定的值“同时”重排，这是个有名的问题。

置换图

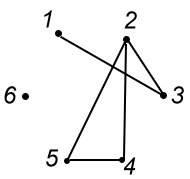
  (2,5,1,4,3,6)的置换图

取一个无向图G，将图G的n个顶点标记v1,...,vn，对应一个置换( s(1) s(2) ... s(n) )，当且仅当s(i) j，则图的vi和vj相连，这样的图称为置换图。

置换图的补图必是置换图。

使用计算机

多数计算机都有个计算置换数的 nPr 键。然而此键在一些最先进的桌上型机种中却被隐藏了。例如：在 TI-83 中，按 MATH、三次右键、再按二。在卡西欧的图形计算机中，按 OPTN，一次右键（F6）、PROB（F3）、nPr（F2）。

试算表语法

多数试算表软件都有函式 PERMUT(Number，Number chosen)，用以计算置换。Number 是描述物件数量的一个整数，Number chosen 是描述每个置换中所取物件数的整数。

C++演算范例

循环法

#includeusingnamespacestd;boolarrsame(int*arr,intlen,intnum){inti;for(i=0;i=n&&i--));if(perm[0]>=n)return0;for(intnum=0,seat=i+1;seat<k;num++)if(!arrsame(perm,i+1,num))perm[seat++]=num;return1;}intmain(){intn,k;cout<<"perm(n,k):"<>n>>k;if(n<k||k<=0)return0;int*perm=newint[k];for(inti=0;i<k;i++)perm[i]=i;dofor(inti=0;i<k;cout<<((++i<k)?",":"\n"))cout<<perm[i]+1;while(next_perm(perm,k,n));delete[]perm;return0;}

递归法

#include#includeusingnamespacestd;namespaceperm{intn,k;intarr[12];intcount;boolarrsame(intsite){for(inti=0;i<site;i++)if(arr[i]==arr[site])return0;return1;}inlinevoidarrprint(){for(inti=0;i<k;i++)printf("%3d",arr[i]);puts("");count++;}voidcalculate(intnow){if(now==k){arrprint();return;}for(inti=0;i<n;i++){arr[now]=i;if(arrsame(now)){calculate(now+1);}}}inlinevoidrun(intnn,intkk){n=nn,k=kk;count=0;if(k=k&&k>0)calculate(0);if(count)printf("\n%d permutation.\n\n",count);elseputs("Input error!");}}intmain(){intn,k;while(scanf("%d%d",&n,&k)!=EOF){perm::run(n,k);fflush(stdout);}return0;}

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。