



朱利亚集合
定义朱利亚集合可以由下式进行反复迭代得到:对于固定的复数c,取某一z值(如z=z0{displaystylez=z_{0}}),可以得到序列这一序列可能发散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的z值的集合称为朱利亚集合。示例下面各图显示了c取不同值时所得到的不同的朱利亚集
定义
朱利亚集合可以由下式进行反复迭代得到:
对于固定的复数c,取某一z值(如 z = z 0 {\displaystyle z=z_{0}} ),可以得到序列
这一序列可能发散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的z值的集合称为朱利亚集合。
示例
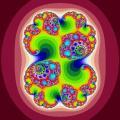
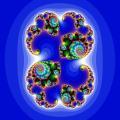
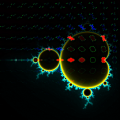
下面各图显示了c取不同值时所得到的不同的朱利亚集合在复平面上的图像:










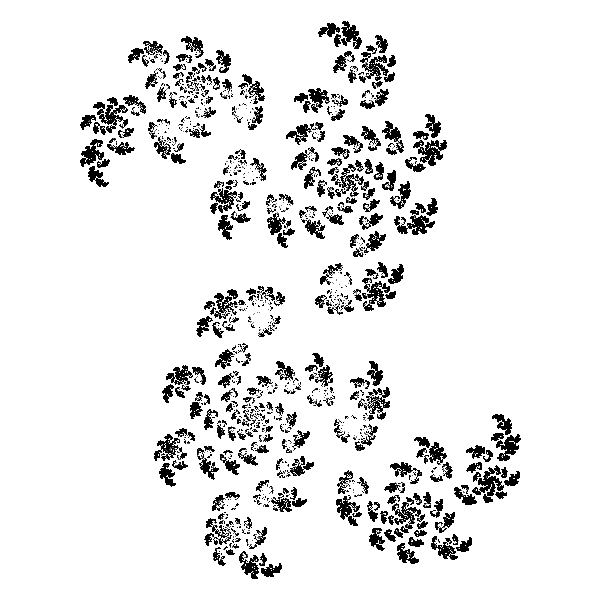











免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 集合

列表在列表中,数据项的顺序是确定的,也可以存在多个相同的数据项。列表支持的操作包括查找项目并找到其位置(若存在),将项目从列表中删除,在特定位置插入项目等。通常的队列,或称FIFO即是一个列表,该列表只能在一端添加项目,而在另一端删除项目。而栈,或LIFO则只能在同一端添加或删除项目。不管是队列还是栈,集合中项目的顺序都应当是一定的,因此这两种情况只是列表的特例。其它列表支持的操作包括排序,再一次说明了其中顺序的重要性。列表的具体形式包括数组,链表等。集与列表不同,在集中,数据项是无序的,也不允许存在相同数据项。集支持添加、删除和查找项目。一些语言内建对集的支持,而在其它语言中,可以利用散列表实现集。多重集多重集的行为类似于集,其中数据项是无序的。但在多重集中,可以存在相同的数据项。多重集支持的操作包括添加、删除项,查询相同项在多重集中出现的次数。多重集可以通过排序转换成列表。关联数组关联
· 集合
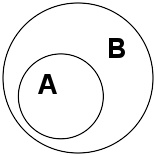
导言定义简单来说,所谓的一个集合,就是将数个对象归类而分成为一个或数个形态各异的大小整体。一般来讲,集合是具有某种特性的事物的整体,或是一些确认对象的汇集。构成集合的事物或对象称作元素或是成员。集合的元素可以是任何事物,可以是人,可以是物,也可以是字母或数字等。在数学交流当中为了方便,集合会有一些别名。比如:族、系通常指它的元素也是一些集合。符号元素通常用a,b,c,d,x{\displaystylea,\b,\c,\d,\x}等小写字母来表示;而集合通常用A,B,C,D,X{\displaystyle\mathbf{A,\B,\C,\D,\X}}等字母来表示。当元素a{\displaystylea}属于集合A{\displaystyle\mathbf{A}}时,记作a∈∈-->A{\displaystylea\in\mathbf{A}}。当元素a{\displaystylea}不属于集合...
· 朱利亚烯烃合成
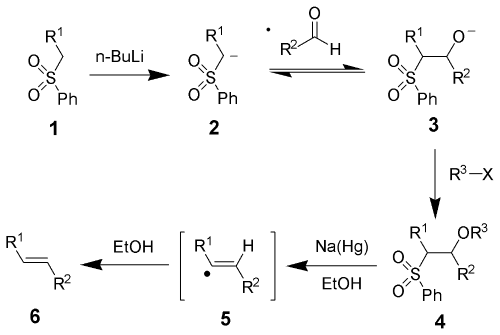
反应机理砜的α-氢具有酸性,在强碱(如正丁基锂、叔丁基锂、甲基锂、二异丙基氨基锂)的作用下失去,得到负离子2,与醛发生加成,生成负离子中间体3。接着3与R3-X反应成酯,经钠汞齐在极性质子溶剂(如甲醇、乙醇)中还原消除,经过自由基机理,生成烯烃6。还原消除一步的详细机理还不是很明确,以前认为是下图中的第一个机理,但1995年时Keck等人发现,如果反应在氘代溶剂中进行,则砜的α-氢几乎被完全氘代,与原来假设的机理不符,故提出了一个新的机理(下图中的第二个机理)。烯烃的立体化学与中间体4无关,无论是苏式还是赤式的反应物经过反应后,都得到反式烯烃。这可能是由于还原时生成的烯基自由基可以自由旋转,从而偏向于热力学稳定产物的缘故。若用二碘化钐作还原剂,反应的立体选择性(E/Z值)明显下降,而且没有上述的氘代现象发生。Keck等人认为其原因是砜基离去后,生成的碳负离子不够稳定,很快就发生消除生成烯烃...
· 集合代数
导言集合代数是研究集合运算和集合关系的基本性质的学科。研究这些性质可以深入探究集合的本质,也有助于实际应用。像普通算术的表达和计算一样,集合的表达和计算可能相当复杂。通过系统研究将有助于熟练使用和理解这些表达方式并进行计算。在算术研究方面,是通过初等代数来研究算术的运算和关系的。例如:加法和乘法运算遵循人们看时候带吃熟知的交换律、结合律和分配律;而"小于等于"关系满足自反性、反对称性和传递性。这些规律提供了简化计算的工具,并描述了算术的本质、运算和关系。集合代数相当于集合论中的算术代数。它是关于集合论运算如交集、并集、补集,和集合论关系如等于、包含等的代数:本文主要介绍这些内容。对集合的基本介绍请参见集合,更详尽的内容请参见朴素集合论。集合上的基本结构集合上通常自然定义的结构包括:这些二元关系和二元运算构成了集合上的基本结构,包括序结构和代数结构。代数结构代数结构是关于运算的结构。以下是集...
· 有界集合
定义如果存在一个实数k,使得对于所有S中的s有k≥s,实数集合S被称为“上有界”的,这个数k被称为S的上界。可用类似的定义术语“下有界”和下界。如果集合S有上界和下界二者,则它是有界的。所以,如果一个实数集合包含在有限区间内,则它是有界的。度量空间度量空间(M,d)的子集S是有界的,如果它包含在有限半径的球内,就是说如果对于所有S中的s,存在M中的x并且r>0,使得d(x,s)<r。M是有界度量空间(或d是有界度量),如果M作为自身的子集是有界的。完全有界性蕴涵有界性。对于R的子集下列二者是等价的。度量空间是紧致的,当且仅当它是完备的并且是完全有界的。欧几里得空间R的子集是紧致的,当且仅当它是闭集并且是有界的。拓扑向量空间内的有界性在拓扑向量空间中,存在一个有界集合的不同定义,通常叫做冯·诺伊曼有界性。如果拓扑向量空间的拓扑是由均匀度量所诱导,如度量是由赋范向量空间的范数所诱导的情况,则这...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















