原理

当光由光密介质（折射率为 n1）入射到光疏介质（折射率为n2）时，入射角为θi则折射角由斯涅尔定律（Snell’s law）可得为θt，可由以下数学式表示：nin⁡ ⁡ -->θ θ -->i=n2sin⁡ ⁡ -->θ θ -->t{\displaystyle n_{1}\sin \theta _{i}=n_{2}\sin \theta _{t}}。

接着改变入射角θi使其慢慢增大，直到折射角θt为90度，我们称此入射角为临界角θc，接着继续增加入射角 θ θ -->i{\displaystyle \theta _{i}} 使其大于临界角 θ θ -->c{\displaystyle \theta _{c}}，全内反射产生全内反射。

在光密介质 n1{\displaystyle n_{1}} 内，反射波与入射波干涉，在界面附近形成驻波，而极小部分的能量会渗入光疏介质 n2{\displaystyle n_{2}} ，电磁场会透出一段距离并沿着界面传播此即为渐逝波。

渐逝波的强度是随着与界面传播的距离成指数衰减的关系，透出一小段距离 δ δ -->z{\displaystyle \delta _{z}} 称为穿透深度（英语：penetration depth）dp（depth of penetration），其定义为当穿透之光波强度减弱至原光波强度的三分之一(1/e=36.8%)时的距离。

δ δ -->z=λ λ -->2π π -->(n1n2)2sin2⁡ ⁡ -->θ θ -->i− − -->1{\displaystyle \delta _{z}={\frac {\frac {\lambda }{2\pi }}{\sqrt {\left({\frac {n_{1}}{n_{2}}}\right)^{2}\sin ^{2}\theta _{i}-1}}}}

采用受抑全内反射的方法可以探测该渐逝波的衰减程度，因此其可用来测量两表面间的距离，进而得知上下两表面的共同粗糙度。

应用

渐逝波在各个领域都有广泛的应用。在光学上特别广泛。 例如利用渐逝波原理制成的分光镜如图。

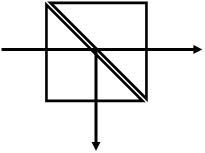
分光镜示意图。

如果只有单片棱镜，光线发生全反射。而使用两片棱镜，改变棱镜间的空气间隙大小，则能改变分光的比例。同样的原理，也可以在光纤的外层上加一光密物质从而得到光纤内部的性质。

参考

电磁波

全内反射

斯涅尔定律

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。