莱布尼兹的发现

这个法则是莱布尼兹发现的，以下是他的证明：设u(x)和v(x)为x的两个可导函数。那么，uv的微分是：

由于du·dv可以忽略不计，因此有：

两边除以dx，便得：

或

例子

假设我们要求出f(x) = xsin(x)的导数。利用乘积法则，可得f"(x) = 2x sin(x) + xcos(x)（这是因为x的导数是2x，sin(x)的导数是cos(x)）。

乘积法则的一个特例，是“常数因子法则”，也就是：如果c是实数，f(x)是可微函数，那么cf(x)也是可微的，其导数为(c × f)"(x) = c × f "(x)。

乘积法则可以用来推出分部积分法和除法定则。

证明一：利用面积

假设

且f和g在x点可导。那么：

现在，以下的差

是图中大矩形的面积减去小矩形的面积。

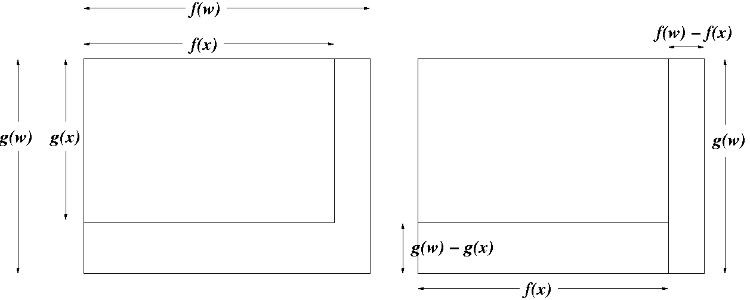
这个区域可以分割为两个矩形，它们面积的和为：

因此，(1)的表达式等于：

如果(5)式中的四个极限都存在，则(4)的表达式等于：

现在：

因为当w → x时，f(x)不变；

因为g在x点可导；

因为f在x点可导；以及

因为g在x点连续（可导的函数一定连续）。

现在可以得出结论，(5)的表达式等于：

证明二：使用对数

设f = uv，并假设u和v是正数。那么：

两边求导，得：

把等式的左边乘以f，右边乘以uv，即得：

证明三：使用导数的定义

设 h(x)=f(x)g(x),{\displaystyle h(x)=f(x)g(x),\,}

且f和g在x点可导。那么：

h′(x)=limΔ Δ -->x→ → -->0h(x+Δ Δ -->x)− − -->h(x)Δ Δ -->x=limΔ Δ -->x→ → -->0f(x+Δ Δ -->x)g(x+Δ Δ -->x)− − -->f(x)g(x)Δ Δ -->x{\displaystyle h"(x)=\lim _{\Delta {x}\to 0}{\frac {h(x+\Delta {x})-h(x)}{\Delta {x}}}=\lim _{\Delta {x}\to 0}{\frac {f(x+\Delta {x})g(x+\Delta {x})-f(x)g(x)}{\Delta {x}}}}

推广

若有n{\displaystyle n}个函数f1,f2,...,fn{\displaystyle f_{1},f_{2},...,f_{n}}，则：

（莱布尼兹法则）若f,g{\displaystyle f,g}均为可导n{\displaystyle n}次的函数，则fg{\displaystyle fg}的n{\displaystyle n}次导数为：

其中(nk){\displaystyle {n \choose k}}是二项式系数。

应用

乘积法则的一个应用是证明以下公式：

其中n是一个正整数（该公式即使当n不是正整数时也是成立的，但证明需要用到其它方法）。我们用数学归纳法来证明这个公式。如果n = 1，ddxx1=limh→ → -->0(x+h)− − -->xh=1=1x1− − -->1{\displaystyle {\frac {d}{dx}}x^{1}=\lim _{h\to 0}{\frac {(x+h)-x}{h}}=1=1x^{1-1}}

假设公式对于某个特定的k成立，那么对于k + 1，我们有：

因此公式对于k + 1也成立。

参见

除法定则

倒数定则

链式法则

分部积分法

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。