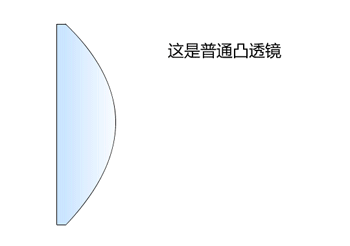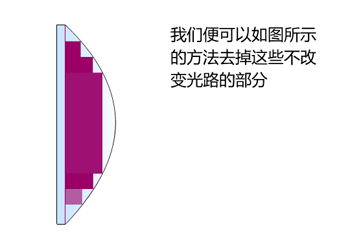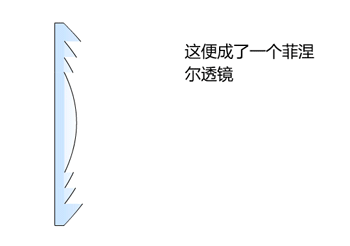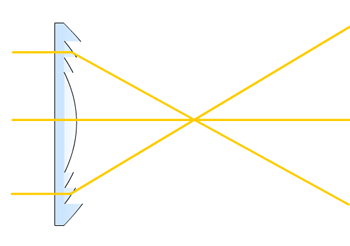
历史通过将数个独立的截面安装在一个框架上从而制作出更轻更薄的透镜，这一想法常被认为是由布封伯爵提出的。孔多塞（1743-1794）提议用单片薄玻璃来研磨出这样的透镜。而法国物理学家兼工程师菲涅耳亦对这种透镜在灯塔上的应用寄予厚望。根据史密森学会的描述，1823年，第一枚菲涅耳透镜被用在了吉伦特河口的哥杜昂灯塔（PharedeCordouan）上；透过它发射的光线可以在20英里（32公里）以外看到。苏格兰物理学家大卫·布儒斯特爵士被看作是促使英国在灯塔中使用这种透镜的推动者。描述菲涅耳透镜的原理演示动画，此为透镜截面视图。由于光的折射发生在介质的交界面，这里以玻璃与空气为例，若能去除光在玻璃中直线传播的部分而保留发生折射的曲面，便能省下大量材料同时达到相同的聚光效果。如图，菲涅耳透镜便是通过此法使透镜变薄。曲面划分得越细，透镜越能够做薄。相比传统的球面透镜，菲涅耳透镜通过将透镜划分出为一系列...

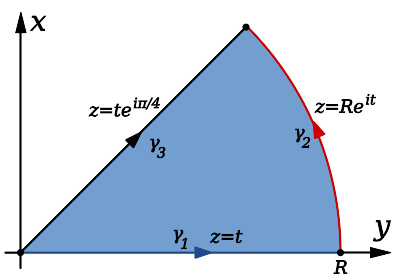
定义菲涅耳积分可由下面两个级数求得，对所有x均收敛。羊角螺线估计值用来计算Fresnelintegrals的扇形路径C和S的值当变数趋近于无穷大时，可用复变分析的方法求得。用以下这个函数的路径积分：在复数平面上的一个扇型的边界，其中下边绕着正x轴，上半边是沿着y=x,x≥0的路径，外圈则是一个半径为R，中心在原点的弧形。当R趋近于无穷大时，路径积分沿弧形的部分将趋近于零，而实数轴部分的积分将可由高斯积分并且经过简单的计算后，第一象限平分线的那条积分便可以变成菲涅耳积分。相关公式下列一些包含菲涅耳积分的关系式∫∫-->0∞∞-->e−−-->atsin(t2){\displaystyle\int_{0}^{\infty}e^{-at}sin(t^{2})}=(1/4)∗∗-->(2)∗∗-->(ππ-->)∗∗-->(cos((1/4)∗∗-->a2)∗∗-->(1−−-->2∗∗-->Fr...

菲涅耳衍射衍射示意图：照射光波于开有孔径的挡板，会在挡板后方区域产生菲涅耳衍射，从而形成波扰于点P。假设照射光波于开有孔径的不透明挡板，则会有衍射图样出现于观察屏。根据惠更斯-菲涅耳原理，从孔径内部任意点次波源Q发射出的圆球面次波，在观察屏点P的波扰ψψ-->(x,y,z){\displaystyle\psi(x,y,z)}为其中，r=(x,y,z){\displaystyle\mathbf{r}=(x,y,z)}是点P的直角坐标，r′=(x′,y′,0){\displaystyle\mathbf{r}"=(x",y",0)}是点Q的直角坐标，λλ-->{\displaystyle\lambda}是波长，S{\displaystyle\mathbb{S}}是积分平面（孔径），ψψ-->(x′,y′,0){\displaystyle\psi(x",y",0)}是位于点次波源...

生平作品1976sybil（心理劫）1977年：《SmokeyandtheBandit》1979年：《诺玛·蕾》1981年：《AbsenceofMalice》1984年：《我心深处》1991年：《Soapdish》1993年：《看狗在说话之旧金山历险记》1993年：《窈窕奶爸》1994年：《阿甘正传》1996年：《逍遙法外》2000年：《女孩第一名》2001年：《芭乐鸳鸯》2003年：《律政俏佳人2》2006年：《生命旅程》2008年：《小美人鱼3：回到当初》2012年：《超凡蜘蛛侠》2012年：《林肯传》2014年：《超凡蜘蛛侠2》2015年：《Hello,mynameisDoris》

连结BlogofAurélieFilippetti(inFrench)