定义

图又有各种变体，包括简单图/多重图;有向图/无向图等，但大体上有以下两种定义方式。

二元组的定义

图 G {\displaystyle G} 是一个二元组 ( V , E ) {\displaystyle (V,E)} ，其中 V {\displaystyle V} 称为顶点集， E {\displaystyle E} 称为边集。它们亦可写成 V ( G ) {\displaystyle V(G)} 和 E ( G ) {\displaystyle E(G)} 。 E {\displaystyle E} 的元素是一个二元组数对，用 ( x , y ) {\displaystyle (x,y)} 表示，其中 x , y ∈ ∈ --> V {\displaystyle x,y\in V} 。

三元组的定义

一个 图 ，是指一个三元组 ( V , E , I ) {\displaystyle (V,E,I)} ，其中 V {\displaystyle V} 称为顶集（Vertices set）， E {\displaystyle E} 称为边集（Edges set）， E {\displaystyle E} 与 V {\displaystyle V} 不相交； I {\displaystyle I} 称为关联函数， I {\displaystyle I} 将 E {\displaystyle E} 中的每一个元素映射到 V × × --> V {\displaystyle V\times V} 。如果 I ( e ) = ( u , v ) ( e ∈ ∈ --> E , u , v ∈ ∈ --> V ) {\displaystyle I(e)=(u,v)(e\in E,u,v\in V)} 那么称边 e {\displaystyle e} 连接顶点 u , v {\displaystyle u,v} ，而 u , v {\displaystyle u,v} 则称作 e {\displaystyle e} 的端点， u , v {\displaystyle u,v} 此时关于 e {\displaystyle e} 相邻。同时，若两条边 i , j {\displaystyle i,j} 有一个公共顶点 u {\displaystyle u} ，则称 i , j {\displaystyle i,j} 关于 u {\displaystyle u} 相邻。

分类

有/无 向图

如果给图的每条边规定一个方向，那么得到的图称为有向图，其边也称为有向边。在有向图中，与一个节点相关联的边有出边和入边之分，而与一个有向边关联的两个点也有始点和终点之分。相反，边没有方向的图称为 无向图 。

简单图

一个图如果

没有两条边，它们所关联的两个点都相同（在 有向图 中，没有两条边的起点终点都分别相同）；

每条边所关联的是两个不同的顶点

多重图

若允许两结点间的边数多于一条，又允许顶点通过同一条边和自己关联，则为多重图的概念。它只能用“三元组的定义”。

基本术语

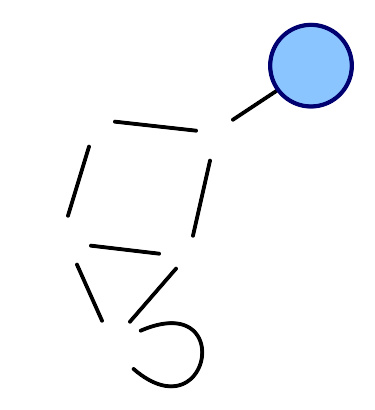
在顶点1有一个环

阶 （Order）：图 G {\displaystyle G} 中顶集 V {\displaystyle V} 的大小称作图 G {\displaystyle G} 的阶。

子图 （Sub-Graph）：图 G ′ {\displaystyle G"} 称作图 G {\displaystyle G} 的子图如果 V ( G ′ ) ⊆ ⊆ --> V ( G ) {\displaystyle V(G")\subseteq V(G)} 以及 E ( G ′ ) ⊆ ⊆ --> E ( G ) {\displaystyle E(G")\subseteq E(G)} 。

生成子图 （Spanning Sub-Graph）：指满足条件 V ( G ′ ) = V ( G ) {\displaystyle V(G")=V(G)} 的 G {\displaystyle G} 的子图 G ′ {\displaystyle G"} 。

度 （Degree）是一个顶点的度是指与该顶点相关联的总边数，顶点 v {\displaystyle v} 的度记作 d ( v ) {\displaystyle d(v)} 。度和边有如下关系： ∑ ∑ --> v ∈ ∈ --> V d ( v ) = 2 | E | {\displaystyle \sum _{v\in V}d(v)=2\left|E\right|} 。

出度 （Out-degree）和 入度 （In-degree）：对有向图而言，顶点的度还可分为出度和入度。一个顶点的出度为 d o {\displaystyle d_{o}} ，是指有 d o {\displaystyle d_{o}} 条边以该顶点为起点，或说与该点关联的出边共有 d o {\displaystyle d_{o}} 条。入度的概念也类似。

邻接矩阵

自环 （Loop）：若一条边的两个顶点相同，则此边称作自环。

路径 （Path）：从顶点u到顶点v的一条路径是指一个序列 v 0 , e 1 , v 1 , e 2 , v 2 , . . . e k , v k {\displaystyle v_{0},e_{1},v_{1},e_{2},v_{2},...e_{k},v_{k}} ， e i {\displaystyle e_{i}} 的起点终点为 v i − − --> 1 {\displaystyle v_{i-1}} 及 v i {\displaystyle v_{i}} ； k {\displaystyle k} 称作路径的长度； v 0 = u {\displaystyle v_{0}=u} ，称为路径的起点； v k = v {\displaystyle v_{k}=v} ，称为路径的终点。如果 u = v {\displaystyle u=v} ，称该路径是 闭 的，反之则称为 开 的；如果 v 1 , . . . , v k {\displaystyle v_{1},...,v_{k}} 两两不等，则称之为 简单路径 （Simple path，注意， u = v {\displaystyle u=v} 是允许的）。

行迹 （Trace）：如果路径 P ( u , v ) {\displaystyle P(u,v)} 中边各不相同，则该路径称为 u {\displaystyle u} 到 v {\displaystyle v} 的一条行迹。

轨道 （Track）：即简单路径。

闭的行迹称作 回路 （Cirt），闭的轨道称作 圈 （Cycle）。

（现存文献中的命名法并无统一标准。比如在另一种定义中，walk对应上述的path，path对应上述的track，trail对应上述的trace。）

距离 （Distance）： 从顶点u出发到顶点v的最短路径若存在，则此路径的长度称作从u到v的距离。若从u到v根本不存在路径，则记该距离为无穷（∞）。

距离矩阵

桥 （Bridge）：若去掉一条边，便会使得整个图不连通，该边称为桥。

图的存储表示

数组（邻接矩阵）存储表示（有向或无向）

邻接表存储表示

前向星存储表示

有向图的十字链表存储表示

无向图的邻接多重表存储表示

一个不带权图中若两点不相邻，邻接矩阵相应位置为0，对带权图（网），相应位置为∞。一个图的邻接矩阵表示是唯一的，但其邻接表表示不唯一。在邻接表中，对图中每个顶点建立一个单链表（并按建立的次序编号），第i个单链表中的结点表示依附于顶点vi的边（对于有向图是以顶点vi为尾的弧）。每个结点由两个域组成：邻接点域（Adjvex），用以指示与vi邻接的点在图中的位置，链域（Nextarc）用以指向依附于顶点vi的下一条边所对应的结点。如果用邻接表存放网（带权图）的信息，则还需要在结点中增加一个存放权值的域（Info）。每个顶点的单链表中结点的个数即为该顶点的出度（与该顶点连接的边的总数）。无论是存储图或网，都需要在每个单链表前设一表头结点，这些表头结点的第一个域data用于存放结点vi的编号i，第二个域firstarc用于指向链表中第一个结点。

图的遍历

图的遍历方法有深度优先搜索法和广度（宽度）优先搜索法。

深度优先搜索法 是树的先根遍历的推广，它的基本思想是：从图G的某个顶点v0出发，访问v0，然后选择一个与v0相邻且没被访问过的顶点vi访问，再从vi出发选择一个与vi相邻且未被访问的顶点vj进行访问，依次继续。如果当前被访问过的顶点的所有邻接顶点都已被访问，则退回到已被访问的顶点序列中最后一个拥有未被访问的相邻顶点的顶点w，从w出发按同样的方法向前遍历，直到图中所有顶点都被访问。其递归算法如下：

Booleanvisited[MAX_VERTEX_NUM];//访问标志数组Status(*VisitFunc)(intv);//VisitFunc是访问函数，对图的每个顶点调用该函数voidDFSTraverse(GraphG,Status(*Visit)(intv)){VisitFunc=Visit;for(v=0;v<G.vexnum;++v)visited[v]=FALSE;//访问标志数组初始化for(v=0;v=0;w=NextAdjVex(G,v,w))//FirstAdjVex返回v的第一个邻接顶点，若顶点在G中没有邻接顶点，则返回空（0）。//若w是v的邻接顶点，NextAdjVex返回v的（相对于w的）下一个邻接顶点。//若w是v的最后一个邻接点，则返回空（0）。if(!visited[w])DFS(G,w);//对v的尚未访问的邻接顶点w调用DFS}

图的 广度优先搜索 是树的按层次遍历的推广，它的基本思想是：首先访问初始点vi，并将其标记为已访问过，接着访问vi的所有未被访问过的邻接点vi1,vi2,…, vi t，并均标记已访问过，然后再按照vi1,vi2,…, vi t的次序，访问每一个顶点的所有未被访问过的邻接点，并均标记为已访问过，依次类推，直到图中所有和初始点vi有路径相通的顶点都被访问过为止。其非递归算法如下：

Booleanvisited[MAX_VERTEX_NUM];// 访问标志数组Status(*VisitFunc)(intv);// VisitFunc是访问函数，对图的每个顶点调用该函数voidBFSTraverse(GraphG,Status(*Visit)(intv)){VisitFunc=Visit;for(v=0;v<G.vexnum;++v){visited[v]=FALSE;}initQueue(Q);// 置空辅助队列Qfor(v=0;v=0;w=NextAdjVex(G,u,w)){if(!Visited[w]){// w为u的尚未访问的邻接顶点Visited[w]=TRUE;VisitFunc(w);EnQueue(Q,w);}}}}}}

图的重要类型

补图：与G拥有相同的点的完全图删除原图G的边所得到的图成为G的补图

树状图

平面图

连通图

有向无环图

完全图：每一对不同顶点间都有边相连的的图，记作 K n {\displaystyle K_{n}} 。

二分图：顶集 V = X ∪ ∪ --> Y ( X ∩ ∩ --> Y = ϕ ϕ --> ) {\displaystyle V=X\cup Y(X\cap Y=\phi )} ，且每一条边都有一个顶点在 X {\displaystyle X} 中，而另一个顶点在 Y {\displaystyle Y} 中。

正则图：如果图中所有顶点的度皆相等，则此图称为正则图

欧拉图:存在经过所有边一次（可以多次经过点）的路径的图

哈密顿图:存在经过所有点一次的路径的图

图的同构

对于图 G ( V , E ) {\displaystyle G(V,E)} 与图 G ′ ( V ′ , E ′ ) {\displaystyle G"(V",E")} ，若存在从 V {\displaystyle V} 到 V ′ {\displaystyle V"} 的一一映射f，使任意 ( u , v ) ∈ ∈ --> E {\displaystyle (u,v)\in E} ,都有 ( f ( u ) , f ( v ) ) ∈ ∈ --> E ′ {\displaystyle (f(u),f(v))\in E"} ，则称 G {\displaystyle G} 与 G ′ {\displaystyle G"} 同构

参考文献

引用

来源

Introduction To Graph Theory , by Gary Chartrand and Ping Zhang, McGraw Hill

参见

图论

邻接矩阵

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。