投影变形

经过投影变形后的世界地图，注意南北极的形状都已经拉长

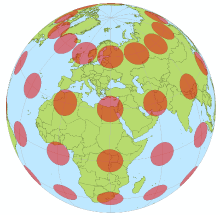
可以用椭圆来说明地图投影的变形

在使用投影时，可以在平面与球面之间建立相对应函数关系，但是经过投影后的平面并不能保持球面上的长度、角度和面积的原形。所以经过投影的地图只能在长度、角度和面积之中的一项不变形，而其他几种变形，只能是变形值相对较小。

通常引进一个椭圆来说明地图投影的变形。在地面上取一个极小的微分圆（面积可以忽略，因此可以看成一个平面），投影变形后将成为一个椭圆，这个椭圆称作“变形椭圆”。利用这个椭圆，可以检验地图投影的变形性质和大小。

长度变形：可以使用长度比μ来表示。长度比是指地面上的微分线段经过投影后的长度与原有长度的比值。值得注意的是，这与比例尺并非一个概念。长度比是一个变量，它随着在地图上位置的变化而变化。

面积变形：可以使用面积比Ρ来表示。面积比是指地面上的微分面积经过投影后的大小与原有大小的比值。面积比也是一个变量。

角度变形：是指地面上的任意两条线的夹角α与经过投影后的角α′的差。由于地面上的一点可以引出无穷条方向线，因此角度变形一般指最大角度变形。

衡量上述投影变形可由下列公式给出 ：

h = 1 R ( ∂ ∂ --> x ∂ ∂ --> ϕ ϕ --> ) 2 + ( ∂ ∂ --> y ∂ ∂ --> ϕ ϕ --> ) 2 {\displaystyle h={\frac {1}{R}}{\sqrt {{{\left({\frac {\partial x}{\partial \phi }}\right)}^{2}}+{{\left({\frac {\partial y}{\partial \phi }}\right)}^{2}}}}}

k = 1 R cos ⁡ ⁡ --> ϕ ϕ --> ( ∂ ∂ --> x ∂ ∂ --> λ λ --> ) 2 + ( ∂ ∂ --> y ∂ ∂ --> λ λ --> ) 2 {\displaystyle k={\frac {1}{R\cos \phi }}{\sqrt {{{\left({\frac {\partial x}{\partial \lambda }}\right)}^{2}}+{{\left({\frac {\partial y}{\partial \lambda }}\right)}^{2}}}}}

sin ⁡ ⁡ --> θ θ --> ′ = 1 h k R 2 cos ⁡ ⁡ --> ϕ ϕ --> ( ∂ ∂ --> y ∂ ∂ --> ϕ ϕ --> ∂ ∂ --> x ∂ ∂ --> λ λ --> − − --> ∂ ∂ --> x ∂ ∂ --> ϕ ϕ --> ∂ ∂ --> y ∂ ∂ --> λ λ --> ) {\displaystyle \sin \theta "={\frac {1}{hk{R^{2}}\cos \phi }}\left({{\frac {\partial y}{\partial \phi }}{\frac {\partial x}{\partial \lambda }}-{\frac {\partial x}{\partial \phi }}{\frac {\partial y}{\partial \lambda }}}\right)}

a ′ = h 2 + k 2 + 2 h k sin ⁡ ⁡ --> θ θ --> ′ {\displaystyle a"={\sqrt {{h^{2}}+{k^{2}}+2hk\sin \theta "}}}

b ′ = h 2 + k 2 − − --> 2 h k sin ⁡ ⁡ --> θ θ --> ′ {\displaystyle b"={\sqrt {{h^{2}}+{k^{2}}-2hk\sin \theta "}}}

a = a ′ + b ′ 2 {\displaystyle a={\frac {a"+b"}{2}}}

b = a ′ − − --> b ′ 2 {\displaystyle b={\frac {a"-b"}{2}}}

s = h k sin ⁡ ⁡ --> θ θ --> ′ {\displaystyle s=hk\sin \theta "}

ω ω --> = 2 arcsin ⁡ ⁡ --> ( b ′ / a ′ ) {\displaystyle \omega =2\arcsin \left({b"/a"}\right)}

其中， x {\displaystyle x} 和 y {\displaystyle y} 为投影平面上的坐标， ϕ ϕ --> {\displaystyle \phi } 和 λ λ --> {\displaystyle \lambda } 为纬度和经度， h {\displaystyle h} 和 k {\displaystyle k} 表示在给定位置沿着纬度线和经度线方向的变形， a {\displaystyle a} 和 b {\displaystyle b} 表示给定位置的最大变形和最小变形，用来表征长度变形， s {\displaystyle s} 用来表征面积变形， ω ω --> {\displaystyle \omega } 用来表征角度变形。

上述公式需要通过微分计算，才能得到 a {\displaystyle a} 、 b {\displaystyle b} 、 s {\displaystyle s} 和 ω ω --> {\displaystyle \omega } ， 用于衡量地图投影的变形。

若不采用微分计算，则可以通过下述公式中的 ρ ρ --> C P ( i ) {\displaystyle {\rho _{CP}}\left(i\right)} ， 近似地衡量角度变形 ω ω --> {\displaystyle \omega } 。

ρ ρ --> C P ( i ) {\displaystyle {\rho _{CP}}\left(i\right)} 被称作互补侧面比率的均值（Averaged ratio between complementary profiles，AveRaComp）。 AveRaComp由两部分构成， ρ ρ --> ~ ~ --> D 3 ( i ) {\displaystyle {{\tilde {\rho }}_{D3}}\left(i\right)} 表征了对角线的长度比， ρ ρ --> ~ ~ --> D 3 ( i ) {\displaystyle {{\tilde {\rho }}_{D3}}\left(i\right)} 表征了对角线之间的夹角。

计算AveRaComp时，首先在投影平面上均匀地划分出 N = n 2 {\displaystyle N=n^{2}} 个网格， 然后，通过逆投影变换，将投影平面上第 i {\displaystyle i} 个网格的四个角点，变换到球面（或椭球体）上，记球面（或椭球体）上的点为 P j {\displaystyle P_{j}} ， j = 1 , ⋯ ⋯ --> , 4 {\displaystyle j=1,\cdots ,4} 。 网格 i {\displaystyle i} 在投影平面上网格的中心点，经过逆投影变换得到的球面（或椭球体）上的点，记作 P ∗ ∗ --> {\displaystyle P_{*}} 。

ω ω --> ≈ ≈ --> ρ ρ --> ~ ~ --> C P ( i ) = [ ρ ρ --> ~ ~ --> D 3 ( i ) + ρ ρ --> ~ ~ --> α α --> ( i ) ] / 2 {\displaystyle \omega \approx {{\tilde {\rho }}_{CP}}\left(i\right)=\left[{{{\tilde {\rho }}_{D3}}\left(i\right)+{{\tilde {\rho }}_{\alpha }}\left(i\right)}\right]/2}

ρ ρ --> ~ ~ --> D 3 ( i ) = max ( | P 1 P ∗ ∗ --> → → --> | + | P ∗ ∗ --> P 3 → → --> | , | P 2 P ∗ ∗ --> → → --> | + | P ∗ ∗ --> P 4 → → --> | ) min ( | P 1 P ∗ ∗ --> → → --> | + | P ∗ ∗ --> P 3 → → --> | , | P 2 P ∗ ∗ --> → → --> | + | P ∗ ∗ --> P 4 → → --> | ) {\displaystyle {{\tilde {\rho }}_{D3}}\left(i\right)={\frac {\max \left({\left|{\overrightarrow {{P_{1}}{P_{*}}}}\right|+\left|{\overrightarrow {{P_{*}}{P_{3}}}}\right|,\left|{\overrightarrow {{P_{2}}{P_{*}}}}\right|+\left|{\overrightarrow {{P_{*}}{P_{4}}}}\right|}\right)}{\min \left({\left|{\overrightarrow {{P_{1}}{P_{*}}}}\right|+\left|{\overrightarrow {{P_{*}}{P_{3}}}}\right|,\left|{\overrightarrow {{P_{2}}{P_{*}}}}\right|+\left|{\overrightarrow {{P_{*}}{P_{4}}}}\right|}\right)}}}

ρ ρ --> ~ ~ --> α α --> ( i ) = cot ⁡ ⁡ --> ( 1 2 arccos ⁡ ⁡ --> | P 1 P 3 → → --> | P 1 P 3 → → --> | ⋅ ⋅ --> P 2 P 4 → → --> | P 2 P 4 → → --> | | ) {\displaystyle {{\tilde {\rho }}_{\alpha }}\left(i\right)=\cot \left({{\frac {1}{2}}\arccos \left|{{\frac {\overrightarrow {{P_{1}}{P_{3}}}}{\left|{\overrightarrow {{P_{1}}{P_{3}}}}\right|}}\cdot {\frac {\overrightarrow {{P_{2}}{P_{4}}}}{\left|{\overrightarrow {{P_{2}}{P_{4}}}}\right|}}}\right|}\right)}

其中， i {\displaystyle i} 为位于投影平面上的给定网格的编号， i = 1 , ⋯ ⋯ --> , N {\displaystyle i=1,\cdots ,N} ， N {\displaystyle N} 为划分网格的总数， P s P t → → --> {\displaystyle {\overrightarrow {{P_{s}}{P_{t}}}}} 表示连接点 P s {\displaystyle P_{s}} 和点 P t {\displaystyle P_{t}} 的向量。

投影方法和分类

投影方法分为几何投影法和数学解析法。几何投影法是按照几何原理绘制的投影变形，适用于比较简单的投影，比如球心正轴方位投影；而数学解析法是利用笛卡尔提出的解析几何理论绘制的投影变形，适用于比较复杂的投影，比如等角正轴方位投影。

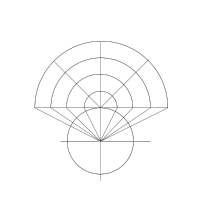
球心正轴方位投影的画法示意图

到目前为止，还没有一个对地图投影分类的统一标准。实际上，通常是按照构成方法或构成性质把地图投影分类。

如果按照构成方法分类，可以分成几何投影和非几何投影。几何投影源于几何透视原理。以几何特征为依据，将地球上的经纬网投影到可以展开的平面（如圆锥、圆柱等）上，可以构成方位投影、圆柱投影（麦卡托投影法）和圆锥投影（亚尔勃斯投影）。非几何投影不借助辅助投影面，用数学解析法求出公式来确立地面与地图上点的函数关系，有伪方位投影、伪圆柱投影、伪圆锥投影（彭纳投影）和多圆锥投影。

按照构成性质分类，可以分为等角投影（正形投影）、等积投影以及任意投影。

目前主要的投影方式主要有方位角（Azimuthal）与方位投影（Azimuthal Equidistant）、正射切面投影（Orthographic）、球心切面投影（Gnomic）、球面透视切面投影（Stereographic）、心状投影（Cordiform）、拟心状投影（Pseudocordiform）、球状投影（Globular）、梯形投影（Trapezoidal）以及椭圆形投影（Oval）。：

格林登投影

麦卡托投影法

亚尔勃斯投影

古德投影

彭纳投影

毛尔威特投影

等角圆柱投影

等距圆锥投影

等角圆锥投影

等积方位投影

等角方位投影

等距投影

等差分纬线多圆锥投影

罗宾森投影

地图投影的应用

制图的区域的位置、形状和范围，地图的比例尺、内容、出版方式影响了投影的种类。比如在极地就应该是正轴方位投影，中纬地区使用正轴圆锥投影。

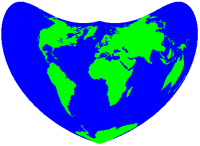
制作世界地图时使用的彭纳投影

制作地形图通常使用高斯－克吕格投影，制作区域图通常使用方位投影、圆锥投影、伪圆锥投影，制作世界地图通常使用多圆锥投影、圆柱投影和伪圆柱投影。但通常而言，要依据实际情况具体选择。

历史

早使用投影法绘制地图的是公元前3世纪古希腊地理学家埃拉托斯特尼，在这之前地图投影曾用来编制星图。他在编制以地中海为中心的当时已知世界地图，应了经纬线互相垂直的等距离圆柱投影。

1569年，佛兰德地图学家尼古拉斯·墨卡托首次采用正轴等角圆柱投影编制航海图，使航海者可以不转换罗盘方向，而采用直线导航。

乔凡尼·多美尼科·卡西尼设计用于三角测量的投影、兰勃特提出的等角投影理论的兰勃特投影和设计出的等角圆锥、等面积方位和等面积圆柱投影，使得十七、十八世纪的地图投影具有时代的特点。

十九世纪，地图投影主要保证大比例尺地图的数学基础，以适应军事制图发展和地形测量扩大的需要，出现德国高斯设计提出的横轴等角椭圆柱投影的高斯投影，这种投影法经德国克吕格尔加以补充，成为高斯-克吕格尔投影。十九世纪末期，俄国一些学者对投影作了较深入地研究，对圆锥投影常数的确定提出了新见解，又提出了根据已知变形分布推求新投影和利用数值法求出投影坐标的新方法。

参考资料

* 周占鳌. 新编地图学教程. 高等教育出版社. ISBN 978-7-04-007263-1.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。