定义

假设一个物理系统符合完整系统的要求，即所有广义坐标都互相独立，则拉格朗日方程成立：

其中，L(q, q˙ ˙ -->, t){\displaystyle {\mathcal {L}}(\mathbf {q} ,\ {\dot {\mathbf {q} }},\ t)\,\!}是拉格朗日量，q=(q1,q2,… … -->,qN){\displaystyle \mathbf {q} =\left(q_{1},q_{2},\ldots ,q_{N}\right)\,\!}是广义坐标，是时间t{\displaystyle t\,\!}的函数，q˙ ˙ -->=(q˙ ˙ -->1,q˙ ˙ -->2,… … -->,q˙ ˙ -->N){\displaystyle {\dot {\mathbf {q} }}=\left({\dot {q}}_{1},{\dot {q}}_{2},\ldots ,{\dot {q}}_{N}\right)\,\!}是广义速度。

导引

在分析力学里，有三种方法可以导引出拉格朗日方程。最原始的方法是使用达朗贝尔原理导引出拉格朗日方程（参阅达朗贝尔原理）；更进阶层面，可以从哈密顿原理推导出拉格朗日方程（参阅哈密顿原理）；最简明地，可以借用数学变分法的欧拉-拉格朗日方程来推导：

设定函数y(x){\displaystyle \mathbf {y} (x)\,\!}和f(y, y˙ ˙ -->, x){\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}：

其中，x{\displaystyle x\,\!}是自变数（independent variable）。

若y(x)∈ ∈ -->(C1[a, b])N{\displaystyle \mathbf {y} (x)\in (C^{1}[a,\ b])^{N}\,\!}使泛函J(y)=∫ ∫ -->abf(y, y˙ ˙ -->, x)dx{\displaystyle J(\mathbf {y} )=\int _{a}^{b}f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)dx\,\!}取得局部平稳值，则在区间(a, b){\displaystyle (a,\ b)\,\!}内，欧拉-拉格朗日方程成立：

现在，执行下述转换：

设定独立变数x{\displaystyle x\,\!}为时间t{\displaystyle t\,\!}、

设定函数yi{\displaystyle y_{i}\,\!}为广义坐标qi{\displaystyle q_{i}\,\!}、

设定泛函f(y, y˙ ˙ -->, x){\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}为拉格朗日量L(q, q˙ ˙ -->, t){\displaystyle {\mathcal {L}}(\mathbf {q} ,\ {\dot {\mathbf {q} }},\ t)\,\!}，

则可得到拉格朗日方程

为了满足这转换的正确性，广义坐标必须互相独立，所以，这系统必须是完整系统。

拉格朗日量是动能减去位势，而位势必须是广义位势。所以，这系统必须是单演系统。

半完整系统

一个不是完整系统的物理系统是非完整系统，不能用上述形式论来分析。假若，一个非完整系统的约束可以以方程表示为

则称此系统为半完整系统。

半完整系统可以用拉格朗日形式论来分析。更具体地说，分析半完整系统必须用到拉格朗日乘子λ λ -->i{\displaystyle \lambda _{i}\,\!}：

其中，λ λ -->i=λ λ -->i(q, q˙ ˙ -->, t){\displaystyle \lambda _{i}=\lambda _{i}(\mathbf {q} ,\ {\dot {\mathbf {q} }},\ t)\,\!}是未知函数。

由于这N{\displaystyle N\,\!}个广义坐标中，有n{\displaystyle n\,\!}个相依的广义坐标，泛函f(y, y˙ ˙ -->, x){\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}不能直接被转换为拉格朗日量L{\displaystyle {\mathcal {L}}\,\!}；必须加入拉格朗日乘子，将泛函f(y, y˙ ˙ -->, x){\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}转换为L+∑ ∑ -->i=1n λ λ -->igi{\displaystyle {\mathcal {L}}+\sum _{i=1}^{n}\ \lambda _{i}g_{i}\,\!}。这样，可以得到拉格朗日广义力方程：

其中，F{\displaystyle {\boldsymbol {\mathcal {F}}}\,\!}是广义力，F=∂ ∂ -->∂ ∂ -->q(∑ ∑ -->i=1n λ λ -->igi)− − -->ddt[∂ ∂ -->∂ ∂ -->q˙ ˙ -->(∑ ∑ -->i=1n λ λ -->igi)]{\displaystyle {\boldsymbol {\mathcal {F}}}={\frac {\partial }{\partial \mathbf {q} }}\left(\sum _{i=1}^{n}\ \lambda _{i}g_{i}\right)-{\frac {d}{dt}}\left[{\frac {\partial }{\partial {\dot {\mathbf {q} }}}}\left(\sum _{i=1}^{n}\ \lambda _{i}g_{i}\right)\right]\,\!}。

这N{\displaystyle N\,\!}个广义力运动方程加上n{\displaystyle n\,\!}个约束方程，给出N+n{\displaystyle N+n\,\!}个方程来解N{\displaystyle N\,\!}个未知广义坐标与n{\displaystyle n\,\!}个拉格朗日乘子。

实例

这个段落会展示拉格朗日方程的两个应用实例。第一个实例展示出，用牛顿方法与拉格朗日方法所得的答案相同。第二个实例展示出拉格朗日方法的威力，因为这问题比较不适合用牛顿方法来分析。

自由落体

思考一个粒子从静止状态自由地下落。由于引力F=mg{\displaystyle F=mg\,\!}作用于此粒子，应用牛顿第二定律，可以得到运动方程

其中，x-坐标垂直于地面，由初始点（原点）往地面指。

这个结果也可以从拉格朗日形式论得到。动能T{\displaystyle T\,\!}是

位势V{\displaystyle V\,\!}是

所以，拉格朗日量L{\displaystyle {\mathcal {L}}\,\!}是

将L{\displaystyle {\mathcal {L}}\,\!}代入拉格朗日方程，

运动方程是

与牛顿方法的运动方程相同。

具有质量的移动支撑点的简单摆

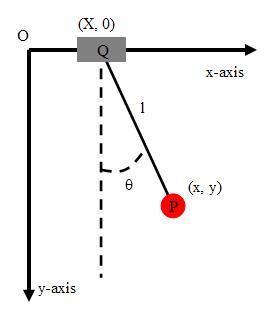
思考一个简单摆系统。系统的x-轴平行于地面，y-轴垂直于x-轴，指向地面。摆锤P的质量是m{\displaystyle m\,\!}，位置是(x, y){\displaystyle (x,\ y)\,\!}。摆绳的长度是l{\displaystyle l\,\!}。摆的支撑点Q的质量是M{\displaystyle M\,\!}。这支撑点Q可以沿着一条平行于x-轴的直线移动。点Q的位置是(X, 0){\displaystyle (X,\ 0)\,\!}。摆绳与y-轴的夹角是θ θ -->{\displaystyle \theta \,\!}。那么，动能是

位势为

所以，拉格朗日量是

两个约束方程为

将约束方程代入拉格朗日量方程,

特别注意，在这里，广义坐标是X{\displaystyle X\,\!}与θ θ -->{\displaystyle \theta \,\!}。应用拉格朗日方程，经过微分运算，对于X{\displaystyle X\,\!}坐标，可以得到

运动方程为

由于拉格朗日量不显含广义坐标X{\displaystyle X\,\!}，称X{\displaystyle X\,\!}为可略坐标，而其相对应的广义动量pX{\displaystyle p_{X}\,\!}是常数K1{\displaystyle K_{1}\,\!}：

对于θ θ -->{\displaystyle \theta \,\!}坐标，可以得到

所以，运动方程为

假如用牛顿第二定律，则必须仔细地辨明所有的相关作用力。这是一项既困难又容易出错的工作。

相关条目

拉格朗日量

拉格朗日力学

哈密顿力学

牛顿力学

变分法

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。