独立的广义坐标

当分析有的问题时（尤其是当有许多约束条件的时候），最好尽量选择独立的广义坐标。因为，这样可以减少代表约束的变数。但是，当遇到非完整约束时，或者当计算约束力时，就必须使用关于这约束力的，相依的广义坐标。

在三维空间里，假设一个物理系统拥有n{\displaystyle n\,\!}颗粒子；那么，这系统的自由度是3n{\displaystyle 3n\,\!}。再假设这系统有h{\displaystyle h\,\!}个完整约束；那么，这系统的自由度变为m=3n− − -->h{\displaystyle m=3n-h\,\!}。必须用m{\displaystyle m\,\!}个独立广义坐标(q1, q2, … … -->, qm){\displaystyle (q_{1},\ q_{2},\ \dots ,\ q_{m})\,\!}与时间t{\displaystyle t\,\!}来完全描述这系统的运动。坐标的转换方程可以表示如下：

虽然我们可能会遇到复杂的系统时，这转换方程具有足够的灵活性来选择最合适的坐标。在思考虚位移与广义力时，这转换方程也可以用来建造微分。

实例

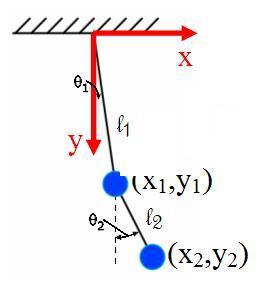
双摆

一个复摆，被约束地移动于一垂直平面，可以用四个直角坐标{x1, y1, x2, y2}{\displaystyle \lbrace x_{1},\ y_{1},\ x_{2},\ y_{2}\rbrace \,\!}来描述。但是，这系统的自由度是2；我们可以用两个广义坐标来更精简地描述这双摆运动：

这里，

一粒珠子，被约束地移动在一条穿过它的铁丝上，自由度是1。它的运动可以用一个广义坐标来描述

这里，s{\displaystyle s\,\!}是珠子离铁丝上一个参考点的径长。这三维空间运动已被减缩为一维空间运动了。

一个物体，被约束在一个表面上，自由度是2；虽然它的运动也是嵌在三维空间里。如果这表面是球表面，一个很好的选择是

这里，θ θ -->{\displaystyle \theta \,\!}与ϕ ϕ -->{\displaystyle \phi 球坐标系}是球坐标系的角坐标。因为r{\displaystyle r\,\!}坐标是常数，可以被忽略掉。

参阅

拉格朗日力学

哈密顿力学

虚功

广义力

广义速度

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。