性质

正方形是正四边形，是特殊的矩形、菱形、对称四边形、平行四边形。其四个内角为直角。除了四边四角相等的性质，正方形还有以下性质：

所有对边平行；

所有内角为直角（ 90 ∘ ∘ --> {\displaystyle 90^{\circ }} ）；

对角线相等且互相垂直平分；

一组对角线平分一组对角；

正方形是圆内接四边形。

面积和周长

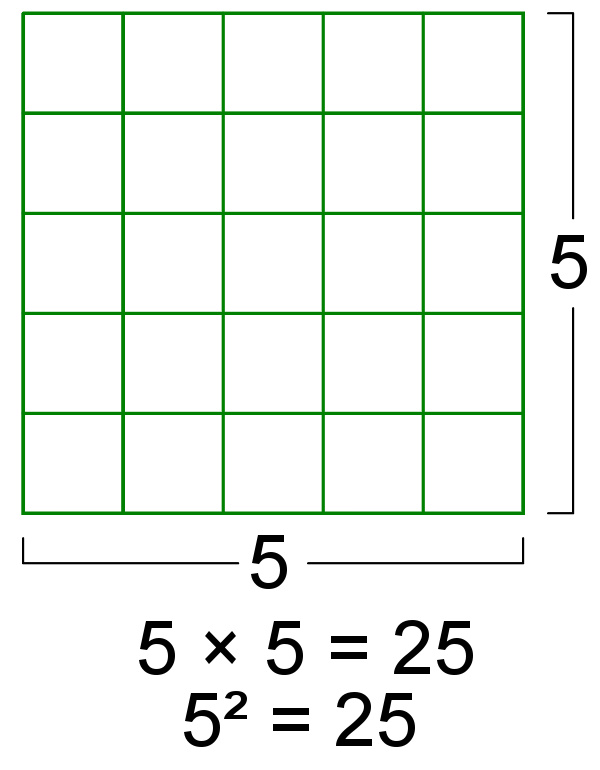
正方形的面积是其边长的平方

正方形的周长是它的边长的 4 倍。如果边长为 a ，那么周长 P = 4 a {\displaystyle P=4a} 。正方形的面积是其边长的平方。如果边长为 a ，那么面积 A = a 2 {\displaystyle A=a^{2}} 。如果我们知道正方形的对角线长 d ，那么我们也可以之计算面积 A = d 2 2 {\displaystyle A={\frac {d^{2}}{2}}} ，如果正方形边心距为r，外接圆半径是R，那么 A = 4 r 2 {\displaystyle A=4r^{2}} 。， A = 2 R 2 {\displaystyle A=2R^{2}} 。

若正方形的边长为整数，其面积就是一个完全平方数。在周长固定时，正方形的面积一定大于其他非正方形的四边形的面积。

对称性

正方形是一种高度对称的平面图形，它关于两条对角线的交点中心对称（这个点又被称作正方形的 中心 ）。它的对称轴有四条，分别是对边中点的连线以及两条对角线。保持正方形不变的变换有8种，包括全等变换，以正方形中心为中心、角度为90度、180度和270度的旋转，以及关于四条对称轴的反射。这八个变换组成了一个群，是二面体群中的一个，记作 D 4 。

正方形与无理数

公元前五世纪时，毕达哥拉斯学派最早证明了正方形的对角线长度与边长长度的比例： 2 {\displaystyle {\sqrt {2}}} ，是无法表示为两个自然数的公比的。

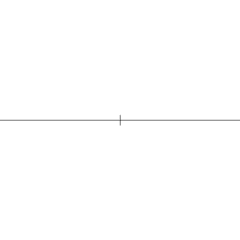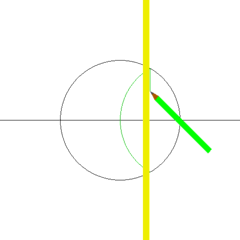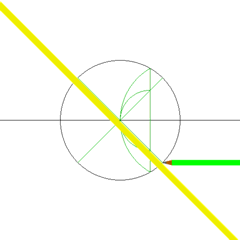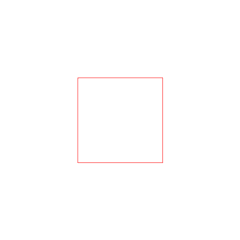
使用圆规与直尺建构出正方形。

平面镶嵌

用同一种多边形不重叠地将平面“铺满”，称为平面的正镶嵌图。正方形是能够组成平面的正镶嵌图的三种正多边形之一（另外两种分别是正三角形和正六边形）。

参见

立方体

根号2

四维超正方体

垂直

圆规四等分圆

幻方

完美正方形

格点

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。