概念

飞轮拥有很大的转动惯量，可以用来使机械运转顺滑。

对于一个质点， I = m r 2 {\displaystyle I=mr^{2}} ，其中 m {\displaystyle m} 是其质量， r {\displaystyle r} 是质点和转轴的垂直距离。

对于一个有多个质点的系统， I = ∑ ∑ --> i = 1 N m i r i 2 {\displaystyle I=\sum _{i=1}^{N}{m_{i}r_{i}^{2}}} 。

对于刚体，可以用无限个质点的转动惯量和，即用积分计算其转动惯量， I = ∫ ∫ --> ρ ρ --> r 2 d V {\displaystyle I=\int {\rho r^{2}}dV} ，其中 ρ ρ --> {\displaystyle \rho } 是密度， d V {\displaystyle dV} 是体积元。

如果一个质量为 m {\displaystyle m} 的物件，以某条经过质心 A {\displaystyle A} 点的直线为轴，其转动惯量为 I A {\displaystyle I_{A}} 。在空间取点 B {\displaystyle B} ，使得 A B {\displaystyle AB} 垂直于原本的轴。那么如果以经过 B {\displaystyle B} 、平行于原本的轴的直线为轴， A B {\displaystyle AB} 的距离为 d {\displaystyle d} ，则 I B = I A + m d 2 {\displaystyle I_{B}=I_{A}+md^{2}} 。

力矩

在直线运动， F = m a {\displaystyle F=ma} 。在旋转运动，则有 τ τ --> = I α α --> {\displaystyle {\tau }=I{\alpha }} ，其中 τ τ --> {\displaystyle {\tau }} 是力矩， α α --> {\displaystyle {\a速度ha }} 是角加速度。

动能

一般物件的动能是 K = 1 2 m v 2 {\displaystyle K={\frac {1}{2}}mv^{2}} 。将速度v和质量m，用转动力学的定义取代：

得出

简化得

如果一个人坐在一张可转动的椅子，双手拿重物，张开双手，转动椅子，然后突然将手缩到胸前，转动的速度将突然增加，因为转动惯量减少了。

惯性张量

对于三维空间中任意一参考点Q与以此参考点为原点的直角坐标系Qxyz，一个刚体的 惯性张量 I {\displaystyle \mathbf {I} \,\!} 是

这里，矩阵的对角元素 I x x {\displaystyle I_{xx}\,\!} 、 I y y {\displaystyle I_{yy}\,\!} 、 I z z {\displaystyle I_{zz}\,\!} 分别为对于x-轴、y-轴、z-轴的 转动惯量 。设定 ( x , y , z ) {\displaystyle (x,\ y,\ z)\,\!} 为微小质量 d m {\displaystyle dm\,\!} 对于点Q的相对位置。则这些转动惯量以方程定义为

矩阵的非对角元素，称为 惯量积 ，以方程定义为

导引

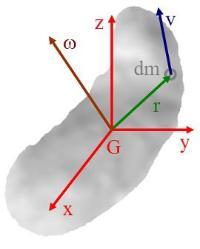
图A

如图A，一个刚体对于质心G与以点G为原点的直角坐标系Gxyz的角动量 L G {\displaystyle \mathbf {L} _{G}\,\!} 定义为

这里， r {\displaystyle \mathbf {r} \,\!} 代表微小质量 d m {\displaystyle dm\,\!} 在Gxyz坐标系的位置， v {\displaystyle \mathbf {v} \,\!} 代表微小质量的速度。因为速度是角速度 ω ω --> {\displaystyle {\boldsymbol {\omega }}\,\!} 叉积位置，所以，

计算x-轴分量，

相似地计算y-轴与z-轴分量，角动量为

如果，我们用方程（1）设定对于质心G的惯性张量 I G {\displaystyle \mathbf {I} _{G}\,\!} ，让角速度 ω ω --> {\displaystyle {\boldsymbol {\omega }}\,\!} 为 ( ω ω --> x , ω ω --> y , ω ω --> z ) {\displaystyle (\omega _{x}\;,\;\omega _{y}\;,\;\omega _{z})\,\!} ，那么，

平行轴定理

平行轴定理能够很简易的，从对于一个以质心为原点的坐标系统的惯性张量，转换至另外一个平行的坐标系统。假若已知刚体对于质心G的惯性张量 I G {\displaystyle \mathbf {I} _{G}\,\!} ，而质心G的位置是 ( x ¯ ¯ --> , y ¯ ¯ --> , z ¯ ¯ --> ) {\displaystyle ({\bar {x}},\ {\bar {y}},\ {\bar {z}})\,\!} ，则刚体对于原点O的惯性张量 I {\displaystyle \mathbf {I} \,\!} ，依照平行轴定理，可以表述为

证明：

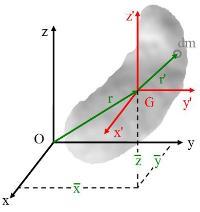
图B

a)参考图B，让 ( x ′ , y ′ , z ′ ) {\displaystyle (x\,",\ y\,",\ z\,")\,\!} 、 ( x , y , z ) {\displaystyle (x,\ y,\ z)\,\!} 分别为微小质量 d m {\displaystyle dm\,\!} 对质心G与原点O的相对位置：

依照方程（2），

所以，

相似地，可以求得 I y y {\displaystyle I_{yy}\,\!} 、 I z z {\displaystyle I_{zz}\,\!} 的方程。

b)依照方程（3），

因为 x = x ′ + x ¯ ¯ --> {\displaystyle x=x\,"+{\bar {x}}\,\!} ， y = y ′ + y ¯ ¯ --> {\displaystyle y=y\,"+{\bar {y}}\,\!} ，所以

相似地，可以求得对于点O的其他惯量积方程。

对于任意轴的转动惯量

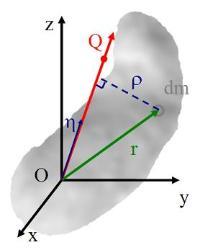
图C

参视图C，设定点O为直角坐标系的原点，点Q为三维空间里任意一点，Q不等于O。思考一个刚体，对于OQ-轴的转动惯量是

这里， ρ ρ --> {\displaystyle \rho \,\!} 是微小质量 d m {\displaystyle dm\,\!} 离OQ-轴的垂直距离， η η --> {\displaystyle {\boldsymbol {\eta }}\,\!} 是沿着OQ-轴的单位矢量， r = ( x , y , z ) {\displaystyle \mathbf {r} =(x,\ y,\ z)\,\!} 是微小质量 d m {\displaystyle dm\,\!} 的位置。

展开叉积，

稍微加以编排，

特别注意，从方程（2）、（3），这些积分项目，分别是刚体对于x-轴、y-轴、z-轴的转动惯量与惯量积。因此，

如果已经知道，刚体对于直角坐标系的三个坐标轴，x-轴、y-轴、z-轴的转动惯量。那么，对于OQ-轴的转动惯量，可以用此方程求得。

主转动惯量

因为惯性张量 I {\displaystyle \mathbf {I} \,\!} 是个实值的三维对称矩阵，我们可以用对角线化，将惯量积变为零，使惯性张量成为一个对角矩阵 。所得到的三个特征值必是正实值；三个特征矢量必定互相正交。

换另外一种方法，我们需要解析特征方程

也就是以下行列式等于零的的三次方程：

这方程的三个根 λ λ --> 1 {\displaystyle \lambda _{1}\,\!} 、 λ λ --> 2 {\displaystyle \lambda _{2}\,\!} 、 λ λ --> 3 {\displaystyle \lambda _{3}\,\!} 都是正实的特征值。将特征值代入方程（8），再加上方向余弦方程，

我们可以求到特征矢量 ω ω --> ^ ^ --> 1 {\displaystyle {\hat {\boldsymbol {\omega }}}_{1}\,\!} 、 ω ω --> ^ ^ --> 2 {\displaystyle {\hat {\boldsymbol {\omega }}}_{2}\,\!} 、 ω ω --> ^ ^ --> 3 {\displaystyle {\hat {\boldsymbol {\omega }}}_{3}\,\!} 。这些特征矢量都是刚体的 惯量主轴 ；而这些特征值则分别是刚体对于惯量主轴的 主转动惯量 。

假设x-轴、y-轴、z-轴分别为一个刚体的惯量主轴，这刚体的主转动惯量分别为 I x {\displaystyle I_{x}\,\!} 、 I y {\displaystyle I_{y}\,\!} 、 I z {\displaystyle I_{z}\,\!} ，角速度是 ω ω --> {\displaystyle {\boldsymbol {\omega }}\,\!} 。那么，角动量为

动能

刚体的动能 K {\displaystyle K\,\!} 可以定义为

这里， v ¯ ¯ --> {\displaystyle {\bar {v}}\,\!} 是刚体质心的速度， v {\displaystyle v\,\!} 是微小质量 d m {\displaystyle dm\,\!} 相对于质心的速度。在方程里，等号右边第一个项目是刚体平移运动的动能，第二个项目是刚体旋转运动的动能 K ′ {\displaystyle K\,\!"\,\!} 。由于这旋转运动是绕着质心转动的，

这里， ω ω --> {\displaystyle {\boldsymbol {\omega }}\,\!} 是微小质量 d m {\displaystyle dm\,\!} 绕着质心的角速度， r {\displaystyle \mathbf {r} \,\!} 是 d m {\displaystyle dm\,\!} 对于质心的相对位置。

应用矢量恒等式，可以得到

或者，用矩阵来表达，

所以，刚体的动能为

假设x-轴、y-轴、z-轴分别为一个刚体的惯量主轴，这刚体的主转动惯量分别为 I x {\displaystyle I_{x}\,\!} 、 I y {\displaystyle I_{y}\,\!} 、 I z {\displaystyle I_{z}\,\!} ，角速度是 ω ω --> {\displaystyle {\boldsymbol {\omega }}\,\!} 。那么，刚体的动能为

计算范例

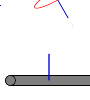
细长棒子的转动惯量是 1 12 m ℓ ℓ --> 2 {\displaystyle {\begin{smallmatrix}{\frac {1}{12}}\,m\ell ^{2}\end{smallmatrix}}}

当自转轴移到末端，转动惯量是 1 3 m ℓ ℓ --> 2 {\displaystyle {\begin{smallmatrix}{\frac {1}{3}}\,m\ell ^{2}\end{smallmatrix}}}

利用线密度 λ λ --> = m ℓ ℓ --> {\displaystyle {\begin{smallmatrix}\lambda ={\frac {m}{\ell }}\end{smallmatrix}}} 可轻易计算出细长棒子沿质心（CM）自转的转动惯量。

当自转轴移到末端，转动惯量变成：

相关条目

横截面的惯性矩：截面二次轴矩

星球质量分布指标：无量纲转动惯量

转动惯量列表

角动量

飞轮矩

参考文献

Beer, Ferdinand; E. Russell Johnston, Jr., William E. Clausen (2004). Vector Mechanics for Engineers. 7th edition. USA: McGraw-Hill, ISBN 978-0-07-230492-3

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。