类型

小角度简单摆

若最高处(v=0)的绳子和最低处(速度最大值)的绳子的角度为 θ θ --> {\displaystyle \theta } ，符合:

θ θ --> ≤ ≤ --> 5 ∘ ∘ --> {\displaystyle \theta \leq 5^{\circ }}

则可使用下列公式算出它的振动周期。

周期公式

T = 2 π π --> L g {\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}}

公式证明

一物体正在摆荡最高处(此时v=0)，绳和中间绳有夹角 θ θ --> {\displaystyle \theta } ，绳长为 L {\displaystyle L} ，相对于中间摆物的位移为 x {\displaystyle x}

此物体受下列力的影响

绳子之拉力大小 F {\displaystyle F}

重力大小 F g = m g {\displaystyle F_{g}=mg}

绳子的拉力 F {\displaystyle F} 有分力

F cos ⁡ ⁡ --> θ θ --> = m g {\displaystyle F\cos \theta =mg}

F sin ⁡ ⁡ --> θ θ --> = k x {\displaystyle F\sin \theta =kx}

∵ ∵ --> lim θ θ --> → → --> 0 cos ⁡ ⁡ --> θ θ --> = 1 {\displaystyle \because {\underset {\theta \to 0}{\mathop {\lim }}}\,\cos \theta =1} ∴ ∴ --> F ≈ ≈ --> m G g {\displaystyle \therefore F\approx m_{G}g} F sin ⁡ ⁡ --> θ θ --> = m G g ( x L ) = k x {\displaystyle F\sin {\theta }=m_{G}g\left({\frac {x}{L}}\right)=kx} 解得 k = m G g L {\displaystyle k={\frac {m_{G}g}{L}}}

代入 T = 2 π π --> m I k {\displaystyle T=2\pi {\sqrt {\frac {m_{I}}{k}}}}

得到 T = 2 π π --> m I L m G g {\displaystyle T=2\pi {\sqrt {\frac {m_{I}L}{m_{G}g}}}}

根据广义相对论可知， m I = m G {\displaystyle m_{I}=m_{G}\,}

故 T = 2 π π --> L g {\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}}

简单摆

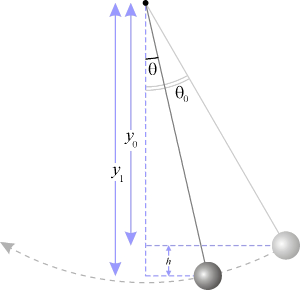
  sin θ 取为θ的误差。

取 L {\displaystyle L} 为绳的长度， θ θ --> {\displaystyle \theta } 为绳和垂直平面的线的交角， θ θ --> 0 {\displaystyle \theta _{0}} 为 θ θ --> {\displaystyle \theta } 的最大值， m {\displaystyle m} 为锤的质量， θ θ --> ¨ ¨ --> {\displaystyle {\ddot {\theta }}} 表示角度加速度 α α --> = d 2 θ θ --> d t 2 {\displaystyle \alpha ={\frac {{\rm {d}}^{2}\theta }{{\rm {d}}t^{2}}}} 。

忽略空气阻力以及绳的弹性、重量的影响：

锤速率最高是在 θ θ --> = 0 {\displaystyle \theta =0} 时。当锤昇到最高点，其速率为 0。绳的张力没有对锤做功，整个过程中动能和位能的和不变。

运动方程为：

注意不论θ的值为何，运动周期和锤的质量无关。

当 θ θ --> {\displaystyle \theta } 相当小的时候， sin ⁡ ⁡ --> θ θ --> ≈ ≈ --> θ θ --> {\displaystyle \sin \theta \approx \theta } ，因此可得到简谐运动常系数微分方程。此为一简谐运动，周期 T = 2 π π --> L g {\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}} 。

准确的运动周期不可以用基础函数求得。考虑微分方程：

将上式重写成第一类椭圆函数的形式：

其中 F ( k , ϕ ϕ --> ) = ∫ ∫ --> 0 ϕ ϕ --> 1 1 − − --> k 2 sin 2 ⁡ ⁡ --> θ θ --> d θ θ --> . {\displaystyle F(k,\phi )=\int _{0}^{\phi }{1 \over {\sqrt {1-k^{2}\sin ^{2}{\theta }}}}\,{\rm {d}}\theta .}

周期可以用级数表示成：

冲击摆

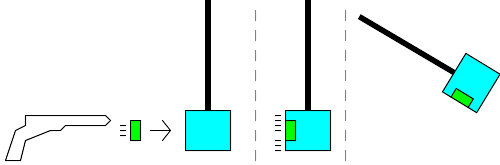
冲击摆是来用计算子弹速度的实验室仪器。它的原理为：物件碰撞前后动量守恒，摆运动时能量守恒。

冲击摆和普通摆相似，特别之处它的锤会和射入子弹产生完全非弹性碰撞，即碰撞后两者会合为一。

将子弹射向停止的锤，使锤和子弹合在一起摆动。设锤质量为 m p {\displaystyle m_{p}\,} ，子弹质量和初速度分别为 m b {\displaystyle m_{b}\,} 和v，锤和子弹碰撞后的速度为u。

以下是子弹速度的计算方法：

由动量守恒定律，

由能量守恒定律，

解得 v = ( m b + m p ) 2 g h m b {\displaystyle v={\frac {(m_{b}+m_{p}){\sqrt {2gh}}}{m_{b}}}} 。

倒单摆

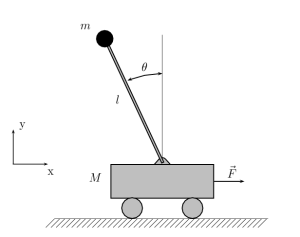
小车上的倒单摆

由一个倒单摆与一个带有水平平带的小车组成的系统。

锥摆

锥摆的路径是平面上圆。摆运动时，绳的路径为一个圆锥面。这是圆周运动。

复摆

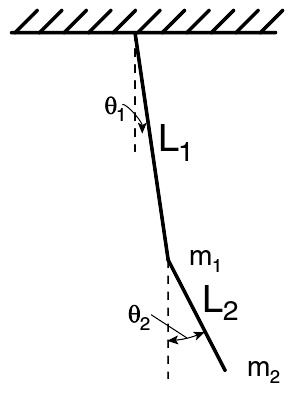
  复摆系统的一例

复摆系统是混沌的。

磁性摆

和复摆一样，磁性摆系统是混沌的。

应用

傅科摆

傅科摆的移动可作为地球自转的证据。

钟摆

摆钟。

为了减少温度变化的影响，有不同的设计：

栅形补偿摆（Gridiron Pendulum）：以不同金属（钢和铜）配搭，保持摆的长度不变[1]

Graham"s pendulum：有一个水银管柱，保持摆的重心不变

以木制摆[2]

Ellicott compensated pendulum：用多个摆的结构配合

参考

en:Pendulum (mathematics)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。