概述

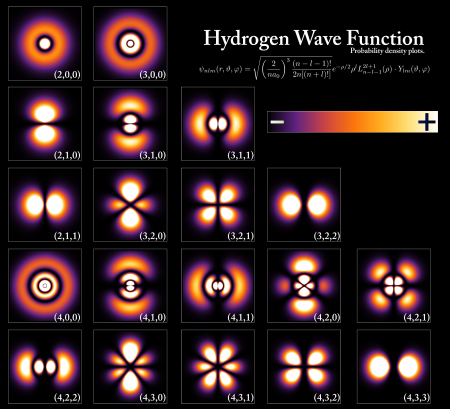
  在不同量子态氢原子的电子概率密度。

经典力学的状态

设想在某经典系统里，有一个粒子移动于一维空间，在时间 t = 0 {\displaystyle t=0} ，粒子的位置 q {\displaystyle q} 是 q 0 {\displaystyle q_{0}} ，动量 p {\displaystyle p} 是 p 0 {\displaystyle p_{0}} 。这些初始条件设定了这系统在时间 t = 0 {\displaystyle t=0} 的状态 σ σ --> 0 {\displaystyle \sigma _{0}} 。经典力学具有决定性，若知道粒子的初始条件与作用于粒子的外力，则可决定粒子的运动行为。

在实验方面，制备经典系统在时间 t = 0 {\displaystyle t=0} 的状态 σ σ --> 0 {\displaystyle \sigma _{0}} 。稍后，在时间 t > 0 {\displaystyle t>0} ，若想知道这系统的物理状态 σ σ --> ( t ) {\displaystyle \sigma (t)} ，可以测量这粒子的运动参数，即位置 q ( t ) {\displaystyle q(t)} 与动量 p ( t ) {\displaystyle p(t)} 。其它物理量，像加速度、动能等等，都是这两个物理量的函数。

在理论方面，假设经典系统在 t = 0 {\displaystyle t=0} 的状态是 σ σ --> 0 {\displaystyle \sigma _{0}} ，则应用牛顿运动定律，即可计算出这系统在任何时间 t > 0 {\displaystyle t>0} 的可观察量数值。这些数值应该符合实验测量的结果。标记这些数值为 p ( t ) {\displaystyle p(t)} 与 q ( t ) {\displaystyle q(t)} 。例如，假设粒子以等速移动，则

其中， m {\displaystyle m} 是粒子质量。

量子力学的量子态

实验的过程可以按照先后顺序细分为制备与测量两个步骤。在统计实验（statistical experiment）里，虽然以同样的方法制备多个物理系统，然后以同样的方法进行测量，仍旧不能可靠地获得出同样的结果，但是，假若经过很多次重复地制备与测量，则会发觉，同样结果的出现频率会收敛至某固定值。量子力学也具有类似特性，虽然每一次测量能够很准确地获得粒子运动地数据，但不能准确预测对于可观察量做单次测量而获得的结果，只能够给出各种可能获得的结果与获得这结果的概率分布，这是因为制备步骤必须遵守不确定性原理。

在量子系统里，量子态可以从一系列制备程序来辨认，即这程序所制成的量子系统拥有这量子态。例如，使用z-轴方向的施特恩-格拉赫实验仪器，可以将入射的银原子束，依照自旋的z-分量 S z {\displaystyle S_{z}} 分裂成两道，一道的 S z {\displaystyle S_{z}} 为上旋，量子态为 | ↑ ↑ --> 〉 〉 --> {\displaystyle |\uparrow \rangle } 或 | z + 〉 〉 --> {\displaystyle |z+\rangle } ，另一道的 S z {\displaystyle S_{z}} 为下旋，量子态为 | ↓ ↓ --> 〉 〉 --> {\displaystyle |\downarrow \rangle } 或 | z − − --> 〉 〉 --> {\displaystyle |z-\rangle } 。又例如，假若等待足够长久时间，就可以使得量子系统衰变至基态，前提是从激发态只能朝着无穷远发射出能量，永远不会反射回来。这样，就可以制备出基态。 再照射适当频率的激光，则可制备出指定的激发态。

在实验方面，量子力学显露出一种内禀统计行为。同样的一个实验重复地做很多次，每次实验的测量结果通常不会一样，只有从很多次的实验结果计算出来的统计平均值，才是可复制的数值。假设，在每次实验里，在时间 t = 0 {\displaystyle t=0} ，量子系统的量子态为 | σ σ --> 0 〉 〉 --> {\displaystyle |\sigma _{0}\rangle } 。稍后，在时间 t > 0 {\displaystyle t>0} ，测量这粒子在各个量子系统的可观察量 q ( t ) {\displaystyle q(t)} 或 p ( t ) {\displaystyle p(t)} ，则能获得在时间 t > 0 {\displaystyle t>0} 这些可观察量的统计平均值。特别注意，对于这两种可观察量并不是一起进行测量，而是独立分开进行测量。更详细地说，重复地做很多次同样的实验，测量可观察量 q ( t ) {\displaystyle q(t)} 。由于这可观察量是随机变量，所以无法可靠地复制同样结果。但是，假若重复次数足够多（概念而言，无穷多），则能获得在时间 t > 0 {\displaystyle t>0} 这可观察量 q ( t ) {\displaystyle q(t)} 的统计平均值。类似地，重复地做很多次同样的实验，测量可观察量 p ( t ) {\displaystyle p(t)} ，也能获得在时间 t > 0 {\displaystyle t>0} 这可观察量 p ( t ) {\displaystyle p(t)} 的统计平均值。

在理论方面，假设量子系统在 t = 0 {\displaystyle t=0} 的量子态是 | σ σ --> 0 〉 〉 --> {\displaystyle |\sigma _{0}\rangle } ，应用埃伦费斯特定理，可以计算出可观察量在任何时间 t > 0 {\displaystyle t>0} 的期望值。这期望值应该完全符合实验获得的统计平均值。标记这些期望值为 〈 〈 --> q ( t ) 〉 〉 --> {\displaystyle \langle q(t)\rangle } 、 〈 〈 --> p ( t ) 〉 〉 --> {\displaystyle \langle p(t)\rangle } 。假设没有任何外力作用于自由移动的粒子，则

位置的期望值与动量的期望值表现出类似经典力学的运动行为。在量子力学里，量子态可以预测所有测量可观察量的实验统计结果。

薛定谔绘景与海森堡绘景

量子系统的每一种可观察量都有其对应的量子算符。将这量子算符作用于量子态，可以诠释为测量其量子系统的可观察量。在前一节量子力学论述里，量子算符 q ( t ) {\displaystyle q(t)} ， p ( t ) {\displaystyle p(t)} 被设定为与时间有关，而量子态则在初始时间 t = 0 {\displaystyle t=0} 就被固定为 | σ σ --> 0 〉 〉 --> {\displaystyle |\sigma _{0}\rangle } ，与时间无关。这种理论方法称为海森堡绘景。另一种称为薛定谔绘景的理论方法设定量子算符与时间无关，又设定量子态与时间有关。在概念方面或在数学方面，这两种绘景等价，推导出的结果一样。大多数初级量子力学教科书采用的是薛定谔绘景，通过生动活泼的量子态，学生可以迅速地了解量子系统如何随着时间演变。海森堡绘景比较适用于研究一些像对称性或守恒定律的基础论题领域，例如量子场论，或者研究超大自由度系统的学术，例如统计力学。

量子力学形式论

量子物理通常使用线性代数来做数学表述。每一种量子系统都有其对应的希尔伯特空间，其量子态都可以用对应的希尔伯特空间里的矢量来表现，这矢量称为态矢量。假若，某态矢量是另外一个态矢量的标量倍数，则这两个态矢量都对应于同样的量子态。因此，态矢量的范数不具有物理意义，只有方向具有物理意义。

假若将态矢量归一化，所有态矢量的范数都等于1，则所有态矢量的集合是希尔伯特空间的单位球。假若，两个归一化态矢量的唯一不同之处是它们的相位因子，则这两个态矢量代表同样的量子态。

狄拉克标记

在量子力学里，数算时常用到线性算符、内积、对偶空间与厄米共轭等概念。为了让运算更加简易、更加抽象，为了让使用者不需要选择表现空间，保罗·狄拉克发明了狄拉克标记。这种标记法能够精准地表示各种各样的量子态与其相关运算，简略表述如下：

矢量的标记形式为 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ；其中 ψ ψ --> {\displaystyle \psi } 可以是任何符号，字母，数字，或单字。这与一般的数学标记形式显然地不同；通常，矢量是以粗体字母，或者在上方加了一个矢号的字母来标记。

称矢量为“右矢”。

对于每一个右矢 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ，都独特地存在一个对应的左矢 〈 〈 --> ψ ψ --> | {\displaystyle \langle \psi |} ，左矢与右矢指的是同一个量子态。在数学里，左矢与右矢分别是彼此的厄米共轭，左矢属于另外一个希尔伯特空间，称为对偶空间。假设右矢 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 的维度为有限值，则可以将右矢写为竖排，左矢写为横排共轭复数的厄米共轭（即取转置运算加上共轭复数运算），就可以得到左矢。

左矢 〈 〈 --> ϕ ϕ --> | {\displaystyle \langle \phi |} 与右矢 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 的内积，可以写为 〈 〈 --> ϕ ϕ --> | ψ ψ --> 〉 〉 --> {\displaystyle \langle \phi |\psi \rangle } 。这内积的物理意义为在量子态 | ϕ ϕ --> 〉 〉 --> {\displaystyle |\phi \rangle } 里找到量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 的概率幅。

量子态的测量

量子理论只能从量子态计算出可观察量的概率分布，因此只能预测可观察量的概率分布，除了一些特别案例之外，不能准确预测（概率小于1）对可观察量做测量获得的数值，这反映出经典物理与量子物理之间的重要差异，在经典力学里，测量的结果本质上是决定性的，而不是概率性的。尽管如此，在量子力学里，对于任意可观察量，必定存在一组本征态。假设量子系统的量子态是其中任意本征态，则测量这量子系统的可观察量得到的数值必定等于其对应的本征值，量子力学可以准确预测这本征值

反过来说，假设给定了量子系统所有可观察量的概率分布，则可决定量子系统的量子态。 但是，决定量子态，并不一定需要所有可观察量的概率分布；大多数时候，只需要给定某些可观察量的概率分布，就可以决定量子态，其它可观察量的概率分布，可以从量子态计算出来。

假设，某量子系统的可观察量标记为 O {\displaystyle O} ，其对应的量子算符 O ^ ^ --> {\displaystyle {\hat {O}}} ，可能有很多不同的本征值 O i {\displaystyle O_{i}} 与对应的本征态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } ，这些本征态 | e i 〉 〉 --> , i = 1 , 2 , 3 , ⋯ ⋯ --> {\displaystyle |e_{i}\rangle ,\quad i=1,\ 2,\ 3,\ \cdots } ，形成了具有正交归一性的基底：

其中， δ δ --> i j {\displaystyle \delta _{ij}} 是克罗内克函数。

描述这量子系统的量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ，可以用这基底表示为

其中， c i = 〈 〈 --> e i | ψ ψ --> 〉 〉 --> {\displaystyle c_{i}=\langle e_{i}|\psi \rangle } 是复系数，是在量子态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } 里找到量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 的概率幅。

重复地做很多次同样的实验，在每次实验里，量子系统的量子态都设定为 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ，则对于每一个量子系统的可观察量 O {\displaystyle O} 做测量，可能得到的结果是各种本征态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } 的本征值 O i {\displaystyle O_{i}} ，获得这些不同结果的次数具有概率性，可以表达为概率分布，结果为 O i {\displaystyle O_{i}} 的概率是 | c i | 2 {\displaystyle |c_{i}|^{2}} 。

假设测量的结果是本征值 O i {\displaystyle O_{i}} ，则可以推断测量后的量子态是本征态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } 。假若立刻再测量可观察量 O {\displaystyle O} ，由于量子态仍旧是本征态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } ，所得到的测量值是本征值 O i {\displaystyle O_{i}} 的概率为1，量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 是“确定态”。

设想另一种可观察量 R {\displaystyle R} ，其对应的算符 R ^ ^ --> {\displaystyle {\hat {R}}} 与算符 O ^ ^ --> {\displaystyle {\hat {O}}} 的对易关系为

称这两种可观察量为不相容可观察量。假若立刻再对本征态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } 测量可观察量 R {\displaystyle R} ，则又会得到统计性的答案。

单粒子系统的基底量子态

离散案例

假设，某量子系统的可观察量标记为 O {\displaystyle O} ，其对应的量子算符 O ^ ^ --> {\displaystyle {\hat {O}}} ，可能有很多不同的本征值 O i {\displaystyle O_{i}} 与对应的本征态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } ，这些本征态 | e i 〉 〉 --> , i = 1 , 2 , 3 , ⋯ ⋯ --> {\displaystyle |e_{i}\rangle ,\quad i=1,\ 2,\ 3,\ \cdots } ，形成了具有正交归一性的基底。 描述这量子系统的量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ，可以用这基底的本征态表示为

其中， c i = 〈 〈 --> e i | ψ ψ --> 〉 〉 --> {\displaystyle c_{i}=\langle e_{i}|\psi \rangle } 是复系数，是在量子态 | e i 〉 〉 --> {\displaystyle |e_{i}\rangle } 里找到量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 的概率幅。

c i {\displaystyle c_{i}} 是 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 与 | e i 〉 〉 --> {\displaystyle |{e_{i}}\rangle } 的内积：

因此， | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 可以表示为

定义投影算符 Λ Λ --> ^ ^ --> i {\displaystyle {\hat {\Lambda }}_{i}} 为

投影算符 Λ Λ --> ^ ^ --> i {\displaystyle {\hat {\Lambda }}_{i}} 作用于量子态，投射出平行于 | e i 〉 〉 --> {\displaystyle |{e_{i}}\rangle } 的部分：

量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 是所有投影部分的总和：

由于量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 可以是任意量子态，因此，基闭包子态具完备性性，或完备性：

其中，在公式最右边的 1 {\displaystyle 1} 代表单位算符。

由于这基底满足正交归一性，

连续案例

位置 x {\displaystyle x} 是一种连续的可观察量，具有连续的本征值谱：

其中， x ^ ^ --> {\displaystyle {\hat {x}}} 是对应于可观察量 x {\displaystyle x} 的算符， | x 〉 〉 --> {\displaystyle |x\rangle } 是本征值为 x {\displaystyle x} 的连续本征态。

对于这连续本征态 | x 〉 〉 --> {\displaystyle |x\rangle } 所组成的基底，必须将前一节提到的离散和，加以修改为积分：

又必须将克罗内克函数改变为狄拉克δ函数：

由于量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 可以是任意量子态，因此，连续基底量子态具有闭包性，或完备性：

由于这基底满足正交归一性，

从这方程，可以推论 | 〈 〈 --> x | ψ ψ --> 〉 〉 --> | 2 d x {\displaystyle |\langle x|\psi \rangle |^{2}\mathrm {d} x} 是粒子处于位置 x {\displaystyle x} 与 x + d x {\displaystyle x+\mathrm {d} x} 之间的概率。

内积 〈 〈 --> x | ψ ψ --> 〉 〉 --> {\displaystyle \langle x|\psi \rangle } 就是波动力学的波函数 ψ ψ --> ( x ) {\displaystyle \psi (x)} ：

态叠加原理

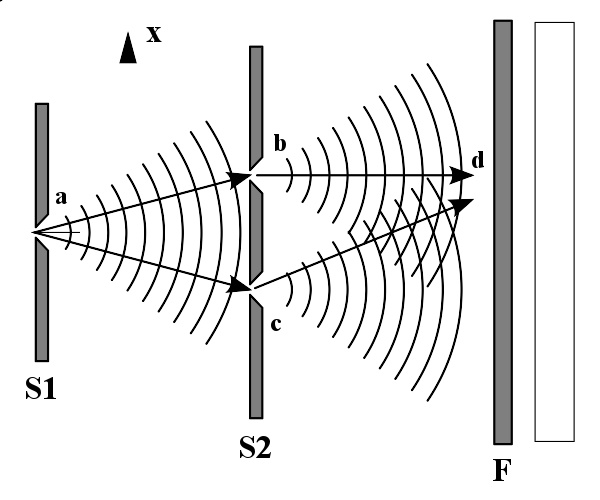
  双缝实验草图，从光源 a {\displaystyle a} 散发出来的单色光，照射在一座有两条狭缝 b {\displaystyle b} 与 c {\displaystyle c} 的不透明挡墙 S 2 {\displaystyle S2} 。在挡墙的后面，设立了一个照相底片或某种侦测屏障 F {\displaystyle F} ，用来纪录到达 F {\displaystyle F} 的任何位置 d {\displaystyle d} 的光波数据。最右边黑白相间的条纹，显示出光波在侦测屏障 F {\displaystyle F} 的干涉图样

假设某量子系统的量子态可能是 | α α --> 〉 〉 --> {\displaystyle |\alpha \rangle } 或 | β β --> 〉 〉 --> {\displaystyle |\beta \rangle } 这两个不同的归一化量子态，则这量子系统也可能处于它们线性叠加而成的量子态 c α α --> | α α --> 〉 〉 --> + c β β --> | β β --> 〉 〉 --> {\displaystyle c_{\alpha }|\alpha \rangle +c_{\beta }|\beta \rangle } （可能尚未归一化）。假设 θ θ --> {\displaystyle \theta } 为实数，则虽然量子态 e i θ θ --> | β β --> 〉 〉 --> {\displaystyle e^{i\theta }|\beta \rangle } 与 | β β --> 〉 〉 --> {\displaystyle |\beta \rangle } 对应于同样的量子态，他们并无法互相替换。例如， | α α --> 〉 〉 --> + | β β --> 〉 〉 --> {\displaystyle |\alpha \rangle +|\beta \rangle } 和 | α α --> 〉 〉 --> + e i θ θ --> | β β --> 〉 〉 --> {\displaystyle |\alpha \rangle +e^{i\theta }|\beta \rangle } 是两个不同的量子态。但是， | α α --> 〉 〉 --> + | β β --> 〉 〉 --> {\displaystyle |\alpha \rangle +|\beta \rangle } 和 e i θ θ --> ( | α α --> 〉 〉 --> + | β β --> 〉 〉 --> ) {\displaystyle e^{i\theta }(|\alpha \rangle +|\beta \rangle )} 对应于同一个量子态。因此可以这样说，整体的相位因子并不具有物理意义，但相对的相位因子具有重要的物理意义。

例如，在双缝实验里，光子的量子态是两个不同量子态的叠加。其中一个量子态是通过狭缝 b {\displaystyle b} 。另外一个量子态是通过狭缝 c {\displaystyle c} 。光子抵达侦测屏障的位置 d {\displaystyle d} ，这位置离开两条狭缝的距离之差值 b d − − --> c d {\displaystyle bd-cd} ，与两个量子态的相对相位有关。由于这相对相位，在侦测屏障的某些位置，会造成相长干涉，在另外一些位置，会造成相消干涉。

再举一个例子，拉比振动，可以显示出相对相位在量子态叠加中的重要性。这是一个双态系统，两个本征态的本征能级不一样。那么，因为态叠加的相对相位随着时间而改变，叠加后的量子态会反复不停地振动于两个本征态。

参阅

量子谐振子

定态

激发态

注释

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。