定义

自1860年以来，许多科学家都在研究此种现象，后来发现布朗运动有下列的主要特性：

粒子的运动由平移及转移所构成，显得非常没规则而且其轨迹几乎是处处没有切线。

粒子之移动显然互不相关，甚至于当粒子互相接近至比其直径小的距离时也是如此。

粒子越小或液体粘性越低或温度越高时，粒子的运动越活泼。

粒子的成分及密度对其运动没有影响。

粒子的运动永不停止。

对于布朗运动之误解

值得注意的是，布朗运动指的是花粉迸出的微粒的随机运动，而不是分子的随机运动。但是通过布朗运动的现象可以间接证明分子的无规则运动。

一般而言，花粉之直径分布于30～50μm、最小亦有10μm之谱，相较之下，水分子直径约0.3nm（非球形，故依部位而有些许差异。），略为花粉的十万分之一。因此，花粉难以产生不规则振动，事实上花粉几乎不受布朗运动之影响。在罗伯特·布朗的手稿中，“tiny particles from the pollen grains of flowers”意味着“自花粉粒中迸出之微粒子”，而非指花粉本身。然而在翻译为诸国语言时，时常受到误解，以为是“水中的花粉受布朗运动而呈现不规则运动”。积非成是之下，在大众一般观念中，此误会已然根深蒂固。

  花粉具备足够大小，几乎无法观测到布朗运动。

在日本，以鹤田宪次‘物理学丛话’为滥觞，岩波书店‘岩波理科辞典’ 、花轮重雄‘物理学読本’、汤川秀树‘素粒子’、坂田昌一‘物理学原论（上）’、平凡社‘理科辞典’、福冈伸一著‘生物与无生物之间’，甚至日本的理科课本等等，皆呈现错误之叙述。

直到1973年横浜市立大学名誉教授植物学者岩波洋造在著书‘植物之SEX‐不为人知的性之世界’中，点出此误谬之前，鲜少有人注意。日本教育研究所物理研究室长板仓圣宣在参与制作岩波电影‘回动粒子’（1970年）时，实际摄影漂浮在水中之花粉，却发现花粉完全没有布朗运动。遂于1975年3月，以“外行人与专家之间”为题，解说有关布朗运动之误会。

爱因斯坦的理论

爱因斯坦的理论有两个部分：第一部分定义布朗粒子扩散方程，其中的扩散系数与布朗粒子平均平方位移相关，而第二部分连结扩散系数与可测量的物理量。以此方式，爱因斯坦可决定原子的大小，一莫耳有多少原子，或气体的克分子量。根据阿伏伽德罗定律，所有理想气体在标准温度和压力积为22.414升，其中包含的原子的数目被称为“阿伏伽德罗常数”。由气体的莫耳质量除以阿伏伽德罗常数等同原子量。 爱因斯坦论点的第一部分是确定布朗粒子在给定的时间内传播距离。古典力学无法确定这个距离，因为一个布朗粒子受到每秒大约10 剧烈碰撞。因此爱因斯坦考虑布朗粒子的集体运动。他表明，如果ρ（x，t）是布朗粒子的密度，在位子x与时间t，则ρ满足扩散方程：

其中D质量扩散系数。

假设在初始时刻t = 0时，所有的粒子从原点开始运动，扩散方程的解

数学模型

定义

满足下列条件的鞅我们称之为布朗运动

这个鞅是关于时间连续的。

他的平方减去时间项也是一个鞅。

( M t ) {\displaystyle (M_{t})} 是一个布朗运动当且仅当 ( M t ) {\displaystyle (M_{t})} 为鞅，且 ( M t 2 − − --> t ) {\displaystyle (M_{t}^{2}-t)} 也为鞅.

其他定义

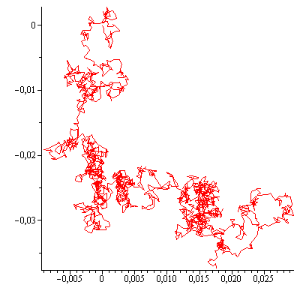
  3000步的2维布朗运动的模拟。

  "> 播放媒体   1000步的3维布朗运动模拟。

一维的定义

一维布朗运动 ( B t ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t})_{t\geq 0}} 是关于时间 t 的一个随机过程，他满足 ：

（独立增量）设时间 t 和 s 满足 t > s ,增量 B t − − --> B s {\displaystyle \scriptstyle B_{t}-B_{s}} 独立于时间 s 前的过程 ( B u ) 0 ≤ ≤ --> u ≤ ≤ --> s {\displaystyle \scriptstyle (B_{u})_{0\leq u\leq s}} 。

（稳定增量和正态性）设时间 t 和 s 满足 t > s ,增量 B t − − --> B s {\displaystyle \scriptstyle B_{t}-B_{s}} 服从均值为0方差为 t − s 的正态分布。

( B t ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t})_{t\geq 0}} 几乎处处连续， 也就是说在任何可能性下， 函数 t ↦ ↦ --> B t ( ω ω --> ) {\displaystyle \scriptstyle t\mapsto B_{t}(\omega )} 是连续的.

通常假设 B 0 = 0 {\displaystyle \scriptstyle B_{0}=0} 。这种布朗运动我们称它为标准的。

等价定义

一维布朗运动 ( B t ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t})_{t\geq 0}} 是关于时间 t 的一个随机过程，他满足 ：

( B t ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t})_{t\geq 0}} 高斯个高斯过程，也就是说对于所有的时间列： t 1 ≤ ≤ --> t 2 ≤ ≤ --> . . . ≤ ≤ --> t n {\displaystyle \scriptstyle t_{1}\leq t_{2}\leq ...\leq t_{n}} ,随机向量： ( B t 1 , B t 2 , . . . , B t n ) {\displaystyle \scriptstyle (B_{t_{1}},B_{t_{2}},...,B_{t_{n}})} 服从高维高斯分布（正态分布）。

( B t ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t})_{t\geq 0}} 几乎处处连续。

对于所有 s 和 t ,均值 E [ B t ] = 0 {\displaystyle \scriptstyle \mathbb {E} [B_{t}]=0} ，协方差 E [ B s B t ] = m i n ( s , t ) {\displaystyle \scriptstyle E[B_{s}B_{t}]=min(s,t)} .

高维定义

换句话说， d 维布朗运动 取值于 R d {\displaystyle \scriptstyle \mathbb {R} ^{d}} ，而它在 R , R 2 , . . . , R d − − --> 1 {\displaystyle \scriptstyle \mathbb {R} ,\mathbb {R} ^{2},...,\mathbb {R} ^{d-1}} 空间上的投影均为布朗运动。

Wiener测度的定义

设 C ( R + , R ) {\displaystyle \scriptstyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )} 为从 R + {\displaystyle \scriptstyle \mathbb {R} ^{+}} 到 R {\displaystyle \scriptstyle \mathbb {R} } 的连续函数空间， ( Ω Ω --> , T , P ) {\displaystyle \scriptstyle (\Omega ,{\mathcal {T}},\mathbb {P} )} 为概率空间。布朗运动为映射

Wiener测度 （或称为布朗运动的分布）设为 W ( d ω ω --> ) {\displaystyle \scriptstyle W(d\omega )} ,是映射 B 关于 P ( d ω ω --> ) {\displaystyle \scriptstyle \mathbb {P} (d\omega )} 的图测度。

换句话说， W 是 C ( R + , R ) {\displaystyle \scriptstyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )} 上的一个概率测度，满足对于任何 A ⊂ ⊂ --> C ( R + , R ) {\displaystyle \scriptstyle A\subset {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )} ，有

备忘

布朗运动是一种增量服从正态分布的莱维过程。

这个定义可以帮助我们证明布朗运动的很多特性，比如几乎处处连续，轨迹几乎处处不可微等等。

我们可以利用二次变差的期望为时间来等价定义布朗运动。这个定义由Levy定理演化而来， 即： 轨迹连续且二次变差为 t {\displaystyle t} 的随机过程为布朗运动。

性质

布朗运动的轨道几乎处处不可微：对于任何 ω ω --> ∈ ∈ --> Ω Ω --> {\displaystyle \scriptstyle \omega \in \Omega } ,轨道 t ↦ ↦ --> B t ( ω ω --> ) {\displaystyle \scriptstyle t\mapsto B_{t}(\omega )} 为一个连续但是零可微的函数。

协方差 E [ B s B t ] = m i n ( s , t ) {\displaystyle \scriptstyle \mathbb {E} [B_{s}B_{t}]=min(s,t)} 。

布朗运动具有强马氏性： 对于停时 T ,取条件 [ T ] {\displaystyle \scriptstyle [T ,过程 ( B t T ) t ≥ ≥ --> 0 := ( B T + t − − --> B T ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t}^{T})_{t\geq 0}:=(B_{T+t}-B_{T})_{t\geq 0}} 为一个独立于 ( B s ) 0 ≤ ≤ --> s < T {\displaystyle \scriptstyle (B_{s})_{0\leq s 的布朗运动。

它的Fourier变换或特征函数为 E [ e i u B t ] = e − − --> t u 2 2 {\displaystyle \scriptstyle \mathbb {E} \left[e^{iuB_{t}}\right]=e^{-{\frac {tu^{2}}{2}}}} 。可见，布朗运动是一个无偏，无跳跃，二项系数为1/2的Levy过程。

布朗运动关于时间是齐次的： 对于 s > 0, ( B t + s − − --> B s ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t+s}-B_{s})_{t\geq 0}} 是一个独立于 ( B u ) 0 ≤ ≤ --> u ≤ ≤ --> s {\displaystyle \scriptstyle (B_{u})_{0\leq u\leq s}} 的布朗运动。

- B 是一个布朗运动。

（稳定性） 对于 c > 0， ( c B t c 2 ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle \left(cB_{\frac {t}{c^{2}}}\right)_{t\geq 0}} 是布朗运动。

（时间可逆性） ( t B 1 t ) t > 0 {\displaystyle \scriptstyle \left(tB_{\frac {1}{t}}\right)_{t>0}} 在 t =0之外是布朗运动。

（常返性）只有1维和2维布朗运动是常返的：

（反射原理）

布朗运动的数学构造

利用Kolmogorov一致性定理

设 ( f t ) t ∈ ∈ --> R + {\displaystyle (f_{t})_{t\in {\mathbb {R} }_{+}}} 为 L 2 ( R + ) {\displaystyle L^{2}({\mathbb {R} }_{+})} 空间中一列实值函数。设：

这列函数满足：

∀ ∀ --> k ∈ ∈ --> N ∗ ∗ --> {\displaystyle \forall k\in \mathbb {N} ^{*}} ，任意的 t 1 , . . . , t k ∈ ∈ --> R + {\displaystyle t_{1},...,t_{k}\in \mathbb {R} _{+}} ,矩阵 ( s ( t i , t j ) ) 1 ≤ ≤ --> i , j ≤ ≤ --> k {\displaystyle \left(s(t_{i},t_{j})\right)_{1\对称q i,j\leq k}} 为对称半正定的。

利用Kolmogorov一致性定理，我们可以构造高斯过程 { Y t } t ∈ ∈ --> R + {\displaystyle \{Y_{t}\}_{t\in \mathbb {R} _{+}}} ，它的均值 m {\displaystyle m} 任意， 协方差为上面定义的 s {\displaystyle s} 。

当 ( f t ) t ∈ ∈ --> R + = ( c .1 1 [ 0 , t ] ) t ∈ ∈ --> R + {\displaystyle (f_{t})_{t\in {\mathbb {R} }_{+}}=\left({\sqrt {c}}.1\!\!1_{[0,t]}\right)_{t\in \mathbb {R} _{+}}} ， c > 0 {\displaystyle c>0} 为不依赖于t的常数， 1 1 [ 0 , t ] {\displaystyle 1\!\!1_{[0,t]}} 为 [ 0 , t ] {\displaystyle [0,t]} 上的示性函数。则：

在这个情况下，矩阵 ( s ( t i , t j ) ) 1 ≤ ≤ --> i , j ≤ ≤ --> k {\displaystyle \left(s(t_{i},t_{j})\right)_{1\leq i,j\leq k}} 是对称且正定的。

我们称一个高斯过程为 布朗运动 当且仅当均值为0，协方差为s。 c = V a r ( B 1 ) {\displaystyle c=Var(B_{1})} ，当 c = 1 {\displaystyle c=1} 时， 称之为 标准的布朗运动 .

利用随机过程

Donsker定理（1951）证明了逐渐归一化的随机游走弱收敛于布朗运动。

其中（ U n , n ≥ 1） 独立同分布， 均值为0,方差为 σ 的随机变量序列。

利用傅立叶级数

设2列独立的正态 N ( 0 , 1 ) {\displaystyle \scriptstyle {\mathcal {N}}(0,1)} 随机变量序列 ( N k , k ∈ ∈ --> N ) {\displaystyle \scriptstyle (N_{k},k\in \mathbb {N} )} 和 ( N k ′ , k ∈ ∈ --> N ) {\displaystyle \scriptstyle (N"_{k},k\in \mathbb {N} )} 。定义 ( B t ) t ≥ ≥ --> 0 {\displaystyle \scriptstyle (B_{t})_{t\geq 0}} ：

为布朗运动。

参见

维纳过程

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。