布灵·杰拉德正规式

对于一般的五次方程式

可以借由以下的转换

得到一个 y {\displaystyle y\,} 的五次多项式，上述的转换称为 契尔恩豪森转换 （ 英语 ： Tschirnhaus transformation ） （Tschirnhaus transformation），借由特别选择的系数 b i {\displaystyle b_{i}\,} ，可以使 y 4 {\displaystyle y^{4}\,} , y 3 {\displaystyle y^{3}\,} , y 2 {\displaystyle y^{2}\,} 的系数为 0 {\displaystyle 0\,} ，从而得到如下的方程式：

以上的化简方法是由 厄兰·塞缪尔·布灵 （ 英语 ： Erland Samuel Bring ） 所发现，后来 乔治·杰拉德 （ 英语 ： George Jerrard ） 也独立发现了此法，因此上式称为 布灵·杰拉德正规式 （ Bring-Jerrard normal form ）。 其步骤如下： 首先令

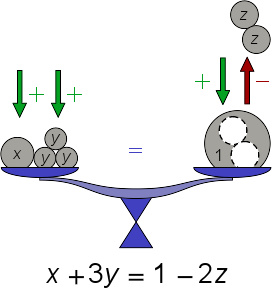
可消去四次方项，得到

其中，

接下来，令 z = y 2 + p y + q {\displaystyle z=y^{2}+py+q\,} ， 得到

再令 P = Q = 0 {\displaystyle P=Q=0\,} ， 求得

第三步，利用契尔恩豪森想到的方法，令：

代入

得到

再令 R = S = T = 0 {\displaystyle R=S=T=0\,} ， 则得 b 4 = 3 A b 1 + 4 B 5 {\displaystyle b_{4}={\frac {3Ab_{1}+4B}{5}}\,} ， 若令 b 2 = − − --> 4 B b 1 + 5 C 3 A {\displaystyle b_{2}=-{\frac {4Bb_{1}+5C}{3A}}\,} ， 则 b 1 {\displaystyle b_{1}\,} ， b 3 {\displaystyle b_{3}\,} 可由以下两个方程解得：

若以函数的观点来看，方程

的解有两个自变数 U {\displaystyle U\,} , 和 V {\displaystyle V\,} 。

若再令

则方程式可以进一步化简为如下形式：

它的解 ξ ξ --> {\displaystyle \xi \,} 是单一变数 t {\displaystyle t\,} 的函数。

特殊五次方程的求根公式

虽然一般的五次方程不存在根式解，但是对于某些特殊的五次方程，满足某些条件后还是有根式解的。

型式1

x 1 = − − --> 2 b + 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f + 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 + 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f − − --> 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 10 a {\displaystyle {x_{1}={\frac {-2b+{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f+16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}+{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f-16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}}{10a}}}\,}

x 2 = − − --> b 5 a + − − --> 1 + 5 + 10 + 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f + 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 + − − --> 1 + 5 − − --> 10 + 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f − − --> 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 {\displaystyle {x_{2}=-{\frac {b}{5a}}+{\frac {-1+{\sqrt {5}}+{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f+16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}+{\frac {-1+{\sqrt {5}}-{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f-16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}}\,}

x 3 = − − --> b 5 a + − − --> 1 − − --> 5 + 10 − − --> 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f + 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 + − − --> 1 − − --> 5 − − --> 10 − − --> 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f − − --> 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 {\displaystyle {x_{3}=-{\frac {b}{5a}}+{\frac {-1-{\sqrt {5}}+{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f+16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}+{\frac {-1-{\sqrt {5}}-{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f-16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}}\,}

x 4 = − − --> b 5 a + − − --> 1 − − --> 5 − − --> 10 − − --> 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f + 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 + − − --> 1 − − --> 5 + 10 − − --> 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f − − --> 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 {\displaystyle {x_{4}=-{\frac {b}{5a}}+{\frac {-1-{\sqrt {5}}-{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f+16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}+{\frac {-1-{\sqrt {5}}+{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f-16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}}\,}

x 5 = − − --> b 5 a + − − --> 1 + 5 − − --> 10 + 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f + 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 + − − --> 1 + 5 + 10 + 2 5 i 40 a 176 b 5 − − --> 1200 a b 3 c + 2000 a 2 b c 2 − − --> 50000 a 4 f − − --> 16 ( 11 b 5 − − --> 75 a b 3 c + 125 a 2 b c 2 − − --> 3125 a 4 f ) 2 − − --> 4 ( 2 b 2 − − --> 5 a c ) 5 5 {\displaystyle {x_{5}=-{\frac {b}{5a}}+{\frac {-1+{\sqrt {5}}-{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f+16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}+{\frac {-1+{\sqrt {5}}+{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{40a}}{\sqrt[{5}]{176b^{5}-1200ab^{3}c+2000a^{2}bc^{2}-50000a^{4}f-16{\sqrt {\left(11b^{5}-75ab^{3}c+125a^{2}bc^{2}-3125a^{4}f\right)^{2}-4\left(2b^{2}-5ac\right)^{5}}}}}}\,}

型式2

x 2 = d [ ( − − --> 1 + 5 ) + 10 + 2 5 i 4 A + ( − − --> 1 − − --> 5 ) + 10 − − --> 2 5 i 4 B ] + d [ ( − − --> 1 − − --> 5 ) − − --> 10 − − --> 2 5 i 4 C + ( − − --> 1 + 5 ) − − --> 10 + 2 5 i 4 D ] {\displaystyle x_{2}=d\left[{\frac {(-1+{\sqrt {5}})+{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{4}}A+{\frac {(-1-{\sqrt {5}})+{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}B\right]+d\left[{\frac {(-1-{\sqrt {5}})-{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}C+{\frac {(-1+{\sqrt {5}})-{\sqrt {10+2{\sqrt {5}}}}{\mathrm {i} }}{4}}D\right]\,}

x 3 = d [ ( − − --> 1 − − --> 5 ) + 10 − − --> 2 5 i 4 A + ( − − --> 1 − − --> 5 ) − − --> 10 − − --> 2 5 i 4 B ] + d [ ( − − --> 1 + 5 ) − − --> 10 + 2 5 i 4 C + ( − − --> 1 + 5 ) + 10 + 2 5 i 4 D ] {\displaystyle x_{3}=d\left[{\frac {(-1-{\sqrt {5}})+{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}A+{\frac {(-1-{\sqrt {5}})-{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}B\right]+d\left[{\frac {(-1+{\sqrt {5}})-{\sqrt {10+2{\sqrt {5}}}}{\mathrm {i} }}{4}}C+{\frac {(-1+{\sqrt {5}})+{\sqrt {10+2{\sqrt {5}}}}{\mathrm {i} }}{4}}D\right]\,}

x 4 = d [ ( − − --> 1 − − --> 5 ) − − --> 10 − − --> 2 5 i 4 A + ( − − --> 1 + 5 ) − − --> 10 + 2 5 i 4 B ] + d [ ( − − --> 1 + 5 ) + 10 + 2 5 i 4 C + ( − − --> 1 − − --> 5 ) + 10 − − --> 2 5 i 4 D ] {\displaystyle x_{4}=d\left[{\frac {(-1-{\sqrt {5}})-{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}A+{\frac {(-1+{\sqrt {5}})-{\sqrt {10+2{\sqrt {5}}}}{\mathrm {i} }}{4}}B\right]+d\left[{\frac {(-1+{\sqrt {5}})+{\sqrt {10+2{\sqrt {5}}}}{\mathrm {i} }}{4}}C+{\frac {(-1-{\sqrt {5}})+{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}D\right]\,}

x 5 = d [ ( − − --> 1 + 5 ) − − --> 10 + 2 5 i 4 A + ( − − --> 1 + 5 ) + 10 + 2 5 i 4 B ] + d [ ( − − --> 1 − − --> 5 ) + 10 − − --> 2 5 i 4 C + ( − − --> 1 − − --> 5 ) − − --> 10 − − --> 2 5 i 4 D ] {\displaystyle x_{5}=d\left[{\frac {(-1+{\sqrt {5}})-{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{4}}A+{\frac {(-1+{\sqrt {5}})+{\sqrt {10+2{\sqrt {5}}}}{\mathrm {i} }}{4}}B\right]+d\left[{\frac {(-1-{\sqrt {5}})+{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}C+{\frac {(-1-{\sqrt {5}})-{\sqrt {10-2{\sqrt {5}}}}{\mathrm {i} }}{4}}D\right]\,}

其中

型式3

a 2 x 5 + 5 a b x 3 + 5 b 2 x + a c = 0 {\displaystyle {a^{2}x^{5}+5abx^{3}+5b^{2}x+ac=0}} ，当 a ≠ ≠ --> 0 {\displaystyle a\neq 0} 时，

x 1 = − − --> c 2 a + ( c 2 a ) 2 + ( b a ) 5 5 + − − --> c 2 a − − --> ( c 2 a ) 2 + ( b a ) 5 5 {\displaystyle {x_{1}={\sqrt[{5}]{-{\frac {c}{2a}}+{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}+{\sqrt[{5}]{-{\frac {c}{2a}}-{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}}\,}

x 2 = − − --> 1 + 5 + 10 + 2 5 i 4 − − --> c 2 a + ( c 2 a ) 2 + ( b a ) 5 5 + − − --> 1 + 5 − − --> 10 + 2 5 i 4 − − --> c 2 a − − --> ( c 2 a ) 2 + ( b a ) 5 5 {\displaystyle {x_{2}={\frac {-1+{\sqrt {5}}+{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}+{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}+{\frac {-1+{\sqrt {5}}-{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}-{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}}\,}

x 3 = − − --> 1 − − --> 5 + 10 − − --> 2 5 i 4 − − --> c 2 a + ( c 2 a ) 2 + ( b a ) 5 5 + − − --> 1 − − --> 5 − − --> 10 − − --> 2 5 i 4 − − --> c 2 a − − --> ( c 2 a ) 2 + ( b a ) 5 5 {\displaystyle {x_{3}={\frac {-1-{\sqrt {5}}+{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}+{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}+{\frac {-1-{\sqrt {5}}-{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}-{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}}\,}

x 4 = − − --> 1 − − --> 5 − − --> 10 − − --> 2 5 i 4 − − --> c 2 a + ( c 2 a ) 2 + ( b a ) 5 5 + − − --> 1 − − --> 5 + 10 − − --> 2 5 i 4 − − --> c 2 a − − --> ( c 2 a ) 2 + ( b a ) 5 5 {\displaystyle {x_{4}={\frac {-1-{\sqrt {5}}-{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}+{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}+{\frac {-1-{\sqrt {5}}+{\sqrt {10-2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}-{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}}\,}

x 5 = − − --> 1 + 5 − − --> 10 + 2 5 i 4 − − --> c 2 a + ( c 2 a ) 2 + ( b a ) 5 5 + − − --> 1 + 5 + 10 + 2 5 i 4 − − --> c 2 a − − --> ( c 2 a ) 2 + ( b a ) 5 5 {\displaystyle {x_{5}={\frac {-1+{\sqrt {5}}-{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}+{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}+{\frac {-1+{\sqrt {5}}+{\sqrt {10+2{\sqrt {5}}}}{\rm {i}}}{4}}{\sqrt[{5}]{-{\frac {c}{2a}}-{\sqrt {\left({\frac {c}{2a}}\right)^{2}+\left({\frac {b}{a}}\right)^{5}}}}}}\,}

参见

方程式论

布灵根式

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。