球面像差公式

一个球面，PA 为由球面顶点到非近轴光线入射点点距离，球面左右介质的折射率分别为 n,n";非近轴入射角，折射角分别为J，J"；非近轴入射线和折射线与光轴的夹角分别为U,U"；近轴光线的入射角为i;这个球面对球面像差的贡献为

球面像差= − − --> 2 ∗ ∗ --> P A ∗ ∗ --> s i n ( − − --> ( 1 / 2 ) ∗ ∗ --> J ′ + ( 1 / 2 ) ∗ ∗ --> J ) ∗ ∗ --> s i n ( ( 1 / 2 ) ∗ ∗ --> J ′ − − --> ( 1 / 2 ) ∗ ∗ --> U ) ∗ ∗ --> n ∗ ∗ --> i ( n ′ ∗ ∗ --> u ′ ∗ ∗ --> s i n ( U ) ) {\displaystyle {\frac {-2*PA*sin(-(1/2)*J"+(1/2)*J)*sin((1/2)*J"-(1/2)*U)*n*i}{(n"*u"*sin(U))}}}

在四种情况下，球面像差为零：

1.

物体和像与球面顶点重合。

2.

物体和物象在球面的曲率中心

3.

4.

在这种情形下的球面成为消球差曲面

根据球面折射的基本方程可以导出 ：

L = r ∗ ∗ --> ( n + n ′ ) n {\displaystyle L={\frac {r*(n+n")}{n}}}

L ′ = r ∗ ∗ --> ( n + n ′ ) n ′ {\displaystyle L"={\frac {r*(n+n")}{n"}}}

对于消球差曲面，凡是射向同一点B入射光，其折射线与光轴相交于一个共同点B"。

B C = L − − --> r = r ∗ ∗ --> n n ′ {\displaystyle BC=L-r=r*{\frac {n}{n"}}}

B C = L ′ − − --> r = r ∗ ∗ --> n ′ n {\displaystyle BC=L"-r=r*{\frac {n"}{n}}}

例如，n=1,n"=1.5 。

L = 2.5 ∗ ∗ --> r {\displaystyle L=2.5*r}

L ′ = 1.6667 ∗ ∗ --> r {\displaystyle L"=1.6667*r}

消球差曲面多用于高倍率显微镜的物镜 。一个消球差薄透镜由一个消球差球面和一个平面经组成，对于平行光。消球差薄透镜等同一块平板玻璃，对于聚合光束，消球差薄透镜增加光束的聚合度，对于发散光束，消球差薄透镜增加光束的发散度。 。

对于一个由多个球面组成镜头，球面像差由一下公式给出 .

LA"=trans+newsp

其中 trans= L A ∗ ∗ --> n [ 1 ] ∗ ∗ --> n ′ [ 1 ] ∗ ∗ --> s i n ( U [ 1 ] ) ( n ′ [ k ] ∗ ∗ --> u ′ [ k ] ∗ ∗ --> s i n ( U ′ [ k ] ) ) {\displaystyle {\frac {LA*n[1]*n"[1]*sin(U[1])}{(n"[k]*u"[k]*sin(U"[k]))}}}

newsp= ∑ ∑ --> k = 1 k ( − − --> 2 ∗ ∗ --> P A ∗ ∗ --> s i n ( − − --> ( 1 / 2 ) ∗ ∗ --> J ′ + ( 1 / 2 ) ∗ ∗ --> J ) ∗ ∗ --> s i n ( ( 1 / 2 ) ∗ ∗ --> J ′ − − --> ( 1 / 2 ) ∗ ∗ --> U ) ∗ ∗ --> n ∗ ∗ --> i ( n ′ [ k ] ∗ ∗ --> u ′ [ k ] ∗ ∗ --> s i n ( U [ k ] ) ) {\displaystyle \sum _{k=1}^{k}({\frac {-2*PA*sin(-(1/2)*J"+(1/2)*J)*sin((1/2)*J"-(1/2)*U)*n*i}{(n"[k]*u"[k]*sin(U[k]))}}}

球面像差展开式

球面像差可表示为

LA"= a ∗ ∗ --> Y 2 + b ∗ ∗ --> Y 4 + c ∗ ∗ --> Y 6 + {\displaystyle a*Y^{2}+b*Y^{4}+c*Y^{6}+} ……………… 。其中Y是入射光线的在球面入射点到光轴的距离。

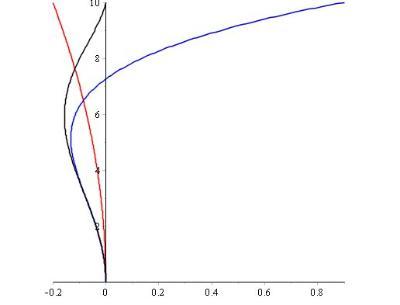
球面像差 红线代表二次项，蓝线代表二次和四次项之和，黑线为二、四、六次项之和

薄透镜组的球面像差

亚历山大·尤金·康拉迪推导出薄透镜组的球面像差公式如下 :

SC= y 4 n 0 ′ ∗ ∗ --> u 0 2 ∗ ∗ --> ∑ ∑ --> ( G 1 ∗ ∗ --> c 3 − − --> G 2 ∗ ∗ --> c 2 ∗ ∗ --> c 1 + G 3 ∗ ∗ --> c 2 ∗ ∗ --> v 1 + G 4 ∗ ∗ --> c ∗ ∗ --> c 1 ∗ ∗ --> v 1 + G 6 ∗ ∗ --> c ∗ ∗ --> v 1 2 ) {\displaystyle {\frac {y^{4}}{n_{0}"*u_{0}^{2}}}*\sum (G_{1}*c^{3}-G_{2}*c^{2}*c_{1}+G_{3}*c^{2}*v_{1}+G_{4}*c*c_{1}*v_{1}+G_{6}*c*v_{1}^{2})} 。

其中“0”代表最后的结果，Σ代表对各镜片之和

薄透镜的球面像差

对于单薄镜片，上式可简化为 。

单镜片的球面像差=LA"= − − --> y 2 ∗ ∗ --> l ′ 2 ∗ ∗ --> ( ∑ ∑ --> ( G 1 ∗ ∗ --> c 3 − − --> G 2 ∗ ∗ --> c 2 ∗ ∗ --> c 1 + G 3 ∗ ∗ --> c 2 ∗ ∗ --> v 1 + G 4 ∗ ∗ --> c ∗ ∗ --> c 1 ∗ ∗ --> v 1 + G 6 ∗ ∗ --> c ∗ ∗ --> v 1 2 ) {\displaystyle -y^{2}*l"^{2}*(\sum (G_{1}*c^{3}-G_{2}*c^{2}*c_{1}+G_{3}*c^{2}*v_{1}+G_{4}*c*c_{1}*v_{1}+G_{6}*c*v_{1}^{2})}

令上式对c_1的导数为零，可求得单镜片具有最小球面像差的条件 :

d L A ′ d c 1 {\displaystyle {\frac {dLA"}{dc_{1}}}} = − − --> y 2 ∗ ∗ --> l ′ 2 ∗ ∗ --> ( − − --> G 2 ∗ ∗ --> c 2 + 2 ∗ ∗ --> G 4 ∗ ∗ --> c ∗ ∗ --> c 1 − − --> G 5 ∗ ∗ --> c ∗ ∗ --> v 1 ) = 0 {\displaystyle -y^{2}*l"^{2}*(-G_{2}*c^{2}+2*G_{4}*c*c_{1}-G_{5}*c*v_{1})=0}

即 c 1 = G 2 c + G 5 v 1 2 G 4 {\displaystyle c_{1}={\frac {G_{2}c+G_{5}v_{1}}{2G_{4}}}} = 0.5 ∗ ∗ --> n ∗ ∗ --> ( 2 ∗ ∗ --> n + 1 ) ∗ ∗ --> c + 2 ∗ ∗ --> ( n + 1 ) ∗ ∗ --> v 1 n + 2 {\displaystyle {\frac {0.5*n*(2*n+1)*c+2*(n+1)*v_{1}}{n+2}}} .

当物距为无穷远时，v_1=0;

于是

c 2 c 1 = r 1 r 2 = 2 n − − --> n − − --> 4 n ∗ ∗ --> ( 2 n + 1 ) {\displaystyle {\frac {c_{2}}{c_{1}}}={\frac {r_{1}}{r_{2}}}={\frac {2n-n-4}{n*(2n+1)}}} 。

参考文献

von Rohr莫里兹·冯·罗尔, Moritz. Geometrical Investigation of the Formation of Images in Optical Instruments. H.M.STATIONARY, LONDON. 1920.

Conrady亚历山大·尤金·康拉迪, Alexander Eugen. applied Optics & Optical design. DOVER PUBLICATION. 1957.

Kingslake鲁道夫·京斯莱克, Rudolf. LENS DESIGN FUNDAMENTALS. ACADEMIC PRESS,NEW YORK. 1978. ISBN 012374301X.

相关条目

像差

哈伯太空望远镜

马克苏托夫望远镜

抛物面反射镜

里奇-克莱琴望远镜（RCT）

施密特修正板

弱聚焦

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。