有限平面

有限平面几何可以分为 仿射 与 射影 两类。在仿射空间中可以探讨线的平行性，射影空间则否。

定义 . 仿射平面 是一个非空集 X {\displaystyle X} （其成员称为 点 ）及一族 X {\displaystyle X} 的子集 L {\displaystyle L} （其成员称为 线 ），使之满足下述条件：

任两点包含于唯一的一条线。

平行公设：给定线 ℓ ℓ --> {\displaystyle \ell } 及点 p ∉ ∉ --> ℓ ℓ --> {\displaystyle p\notin \ell } ，存在唯一的线 ℓ ℓ --> ′ {\displaystyle \ell "} 使之包含 p {\displaystyle p} 且 ℓ ℓ --> = ℓ ℓ --> ′ {\displaystyle \ell =\ell "} 或 ℓ ℓ --> ∩ ∩ --> ℓ ℓ --> ′ = ∅ ∅ --> {\displaystyle \ell \cap \ell "=\emptyset } 。

存在四个点，其中任三点不共线。

最后一条公设保证几何非空，前两条公设确定了几何的性质。

最简单的仿射平面由四点构成，其中任两点决定唯一一条线，所以此平面有四条线。这可以设想为四面体的顶点与边。

一般而言， n {\displaystyle n} 阶仿射平面有 n 2 {\displaystyle n^{2}} 个点与 n 2 + n {\displaystyle n^{2}+n} 条线；每条线含 n {\displaystyle n} 点，每点落于 n + 1 {\displaystyle n+1} 条线。

定义 . 射影平面 是一个非空集 X {\displaystyle X} （其成员称为 点 ）及一族 X {\displaystyle X} 的子集 L {\displaystyle L} （其成员称为 线 ），使之满足下述条件：

任两点包含于唯一的一条线。

任两条相异的线交于唯一一点。

存在四个点，其中任三点不共线。

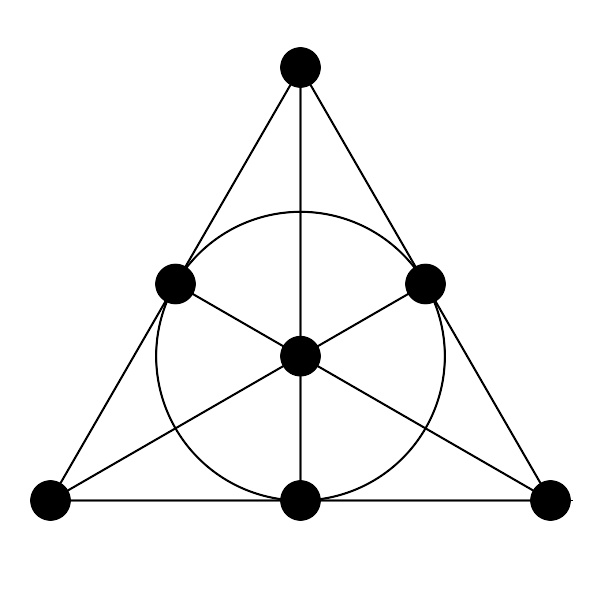
Fano 平面的图解

在上述公理中，我们可以交换点及线的角色，这蕴含了射影几何的 对偶性 ：若射影几何的某命题成立，则将命题中的点与线互换后，新命题依然成立。

最简单的射影平面称作 Fano 平面，又称二阶射影平面，由七条线及七个点构成。若除去任一直线（及其上之点），将得到二阶仿射平面。

一般而言， n {\displaystyle n} 阶射影平面的点、线个数均为 n 2 + n + 1 {\displaystyle n^{2}+n+1} ，每条线含 n + 1 {\displaystyle n+1} 个点，每个点落于 n + 1 {\displaystyle n+1} 条线。

对任意正整数 n {\displaystyle n} ， n {\displaystyle n} 阶射影或仿射平面的存在性至今未解。一般的猜想是这种几何存在当且仅当 n {\displaystyle n} 是素数幂。

有限几何的对称群

若一映射 f : X → → --> X {\displaystyle f:X\to X} 保存共线关系，则称之为 X {\displaystyle X} 的 对称 （或 自同构 ）。Fano 平面的对称群同构于 P S L ( 2 , F 7 ) {\displaystyle \mathrm {PSL} (2,\mathbb {F} _{7})} ，有 168 {\displaystyle 168} 个元素。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。