表示方法

向量由方向和程度（或：长度）两个因素所组成，可以记为 a → → --> {\displaystyle {\vec {a}}} 。

一些书本向量会用粗体字母表示，如 v {\displaystyle \mathbf {v} } ，要区分是否粗体字有时不容易，例如 D {\displaystyle \!\mathrm {D} } 和 D {\displaystyle \!\mathbf {D} } 肉眼看易混淆。

向量的直观图形表示则一般使用带箭头的线段。而遇到某些特殊情况需要表示与记载纸面垂直的向量，则会使用圆圈中打叉或打点的方式来表示（如右图）。圆圈中带点的记号（⊙）表示由纸下方指向纸上方的向量，而圆圈中带叉的记号（⊗）则表示由纸的上方指向纸下方的向量。由于这种记号不表示向量的大小，所以必须时需要在旁边或其它地方另外注明。

 

在直角坐标系中，定义有若干个特殊的基本向量，其它的向量可以通过这些基本向量来表示。在常见的三维空间直角坐标系Oxyz里，基本向量就是以横轴（Ox）、竖轴（Oy） 以及纵轴（Oz） 为方向的三个单位向量 i → → --> {\displaystyle {\vec {i}}} 、 j → → --> {\displaystyle {\vec {j}}} 、 k → → --> {\displaystyle {\vec {k}}} 。这三个向量取好以后，其它的向量就可以通过三元数组来表示，因为它们可以表示成一定倍数的三个基本向量的总合。比如说一个标示为（2,1,3）的向量就是2个向量 i → → --> {\displaystyle {\vec {i}}} 加上1个向量 j → → --> {\displaystyle {\vec {j}}} 加上3个向量 k → → --> {\displaystyle {\vec {k}}} 得到的向量。

在进行矩阵运算时，向量也可以表达成列向量和行向量，在线性代数运算将会有差异（如下例)。

简介

物理学和一般的几何学中涉及的向量概念严格意义上应当被称为欧几里得向量或几何向量，因为它们的定义是建立在通常所说的欧几里得空间上的。按照定义，欧几里得向量由大小和方向构成。在线性代数中，向量是所谓向量空间中的基本构成元素。向量空间是基于物理学或几何学中的空间概念而形成的一个抽象概念，是满足一系列法则的元素的集合。欧几里得空间便是线性空间的一种。向量空间中的元素就可以被称为向量，而欧几里得向量则是特指欧几里得空间中的向量。

在一些上下文中，会假设向量有确定的起点和终点，当起点和终点改变后，构成的向量就不再是原来的向量。这样的向量也被称为固定向量。在另一些时候，会认为向量的起点和终点并不那么重要。两个起点不一样的向量，只要大小相等，方向相同，就可以称为是同一个向量。这样的向量被称为自由向量。在数学中，一般只研究自由向量，也就是起点可以不同，只要大小以及方向一样，即可视为同一向量，与向量的起始点并无关系。一些文献中会提到向量空间带有一个特定的原点，这时可能会默认向量的起点是原点。

例子

一维向量

某人家门口是一条南北向的道路。他散步时先向南行走100米，那么他位置的移动就可以用一个大小为100米，方向为南的向量来表示。之后他再向北走300米，这一次的移动可以用一个大小为300米，方向为北的向量来表示。散步的人总共相对于他家的位移则可以用大小为200米，方向为北的向量来表示。几何学上看来，这些向量都在同一条一维的直线上，只有两个互相平行的方向。

物理学的例子

在物理学中，许多常见的量都是用矢量描述，例如运动学中的位移、速度、加速度，力学中的力、力矩，电磁学中的电流密度、磁矩、电磁波等等。其中矢量的大小不一定是表示长度，还可以表示力的大小、电场或磁场的强弱等等。

附属名词

与数字一样，一个向量中也有反向量、零向量、等向量...等量值。

反向量

一个向量 u → → --> {\displaystyle {\vec {u}}} 的反向量与它大小相等，但方向相反，一般记作 − − --> u → → --> {\displaystyle -{\vec {u}}} 。如果向量 a → → --> {\displaystyle {\vec {a}}} 是向量 b → → --> {\displaystyle {\vec {b}}} 的反向量，那么 b → → --> {\displaystyle {\vec {b}}} 也是 a → → --> {\displaystyle {\vec {a}}} 的反向量。

零向量

始点与终点重合，也就是重合点的向量。 0 → → --> = A A → → --> = B B → → --> = . . {\displaystyle {\vec {0}}={\overrightarrow {AA}}={\overrightarrow {BB}}=..} 。，具有方向性，但方向不定。。因此，零向量与任一向量平行。

等向量

两向量长度、方向相等，即为等向量

有向线段

一个以点A为起点，B为终点的有向线段。

有向线段的概念建构于向量的方向与长度，差别在于多定义了始点与终点。在文字描述时，如果已知某有向线段的起点和终点分别是A和B，此线段的长度可以记为 | A B → → --> | {\displaystyle |{\overrightarrow {AB}}|} ，即 | A B → → --> | = A B ¯ ¯ --> {\displaystyle |{\overrightarrow {AB}}|={\overline {AB}}} 。

数量积

数量积也叫点积，它是向量与向量的乘积，其结果为一个标量（非向量）。几何上，数量积可以定义如下：

设 A → → --> {\displaystyle {\vec {A}}} 、 B → → --> {\displaystyle {\vec {B}}} 为两个任意向量，它们的夹角为 θ θ --> {\displaystyle \theta } ，则他们的数量积为：

即 A → → --> {\displaystyle {\vec {A}}} 向量在 B → → --> {\displaystyle {\vec {B}}} 向量方向上的投影长度（同方向为正反方向为负号），与 B → → --> {\displaystyle {\vec {B}}} 向量长度的乘积。 数量积被广泛应用于物理中，如做功就是用力的向量乘位移的向量，即 W = F → → --> ⋅ ⋅ --> s → → --> {\displaystyle W={\vec {F}}\cdot {\vec {s}}} 。

向量积

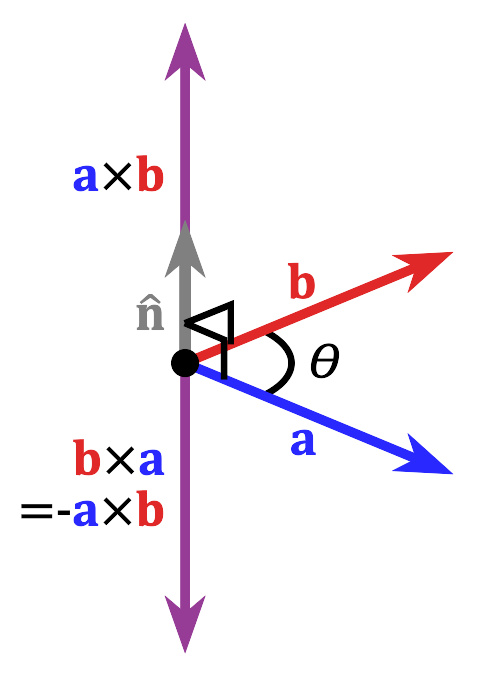
向量积也叫叉积，外积，它也是向量与向量的乘积，不过需要注意的是，它的结果是个向量。它的几何意义是所得的向量与被乘向量所在平面垂直，方向由右手定则规定，大小是两个被乘向量张成的平行四边形的面积。所以向量积不满换律。举例来说 ( 1 , 0 , 0 ) × × --> ( 0 , 1 , 0 ) = ( 0 , 0 , 1 ) {\displaystyle (1,0,0)\times (0,1,0)=(0,0,1)} 但是 ( 0 , 1 , 0 ) × × --> ( 1 , 0 , 0 ) = ( 0 , 0 , − − --> 1 ) {\displaystyle (0,1,0)\times (1,0,0)=(0,0,-1)} 。

设有向量 A → → --> = ( A x i → → --> , A y j → → --> , A z k → → --> ) {\displaystyle {\vec {A}}=(A_{x}{\vec {i}},A_{y}{\vec {j}},A_{z}{\vec {k}})} 、 B → → --> = ( B x i → → --> , B y j → → --> , B z k → → --> ) {\displaystyle {\vec {B}}=(B_{x}{\vec {i}},B_{y}{\vec {j}},B_{z}{\vec {k}})} ，

则其向量积的矩阵表达式可用下列符号表示：

混合积

三个向量 a → → --> {\displaystyle {\vec {a}}} 、 b → → --> {\displaystyle {\vec {b}}} 和 c → → --> {\displaystyle {\vec {c}}} 的混合积定义为，物理意义为三向量始于同点时所构成的体积：

线性相关性

对于 m {\displaystyle m} 个向量 v → → --> 1 {\displaystyle {\vec {v}}_{1}} ， v → → --> 2 {\displaystyle {\vec {v}}_{2}} ，…， v → → --> m {\displaystyle {\vec {v}}_{m}} ，如果存在一组不全为零的 m {\displaystyle m} 个数 a 1 {\displaystyle a_{1}} 、 a 2 {\displaystyle a_{2}} 、…、 a m {\displaystyle a_{m}} ，使得 ∑ ∑ --> i = 1 m a i v → → --> i = 0 → → --> {\displaystyle \sum _{i=1}^{m}{a_{i}{\vec {v}}_{i}}={\vec {0}}} ，那么，称 m {\displaystyle m} 个向量 v → → --> 1 {\displaystyle {\vec {v}}_{1}} ， v → → --> 2 {\displaystyle {\vec {v}}_{2}} ，…， v → → --> m {\displaystyle {\vec {v}}_{m}} 线性相关。如果这样不全为零的 m {\displaystyle m} 个数不存在，即上述向量等式仅当 a 1 {\displaystyle a_{1}} = a 2 {\displaystyle a_{2}} = … = a m {\displaystyle a_{m}} = 0时才能成立，就称向量 v → → --> 1 {\displaystyle {\vec {v}}_{1}} ， v → → --> 2 {\displaystyle {\vec {v}}_{2}} ，…， v → → --> m {\displaystyle {\vec {v}}_{m}} 线性无关。

向量运算

向量的大小是相对的，在有需要时，会规定单位向量，以其长度作为1。每个方向上都有一个单位向量。

向量之间可以如数字一样进行运算。常见的向量运算有：加法，减法，数乘向量以及向量之间的乘法（数量积和向量积）。

加法与减法

向量的加法满足平行四边形法则和三角形法则。具体地，两个向量 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} 相加，得到的是另一个向量。这个向量可以表示为 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} 的起点重合后，以它们为邻边构成的平行四边形的一条对角线（以共同的起点为起点的那一条，见下图左），或者表示为将 a → → --> {\displaystyle {\vec {a}}} 的终点和 b → → --> {\displaystyle {\vec {b}}} 的起点重合后，从 a → → --> {\displaystyle {\vec {a}}} 的起点指向 b → → --> {\displaystyle {\vec {b}}} 的终点的向量：

320px

两个向量 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} 的相减，则可以看成是向量 a → → --> {\displaystyle {\vec {a}}} 加上一个与 b → → --> {\displaystyle {\vec {b}}} 大小相等，方向相反的向量。又或者， a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} 的相减得到的向量可以表示为 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} 的起点重合后，从 b → → --> {\displaystyle {\vec {b}}} 的终点指向 a → → --> {\displaystyle {\vec {a}}} 的终点的向量：

180px

当这两个向量数值、方向都不同，基本向量 e → → --> 1 = ( 1 , 0 , 0 ) , e → → --> 2 = ( 0 , 1 , 0 ) , e → → --> 3 = ( 0 , 0 , 1 ) {\displaystyle {\vec {e}}_{1}=(1,0,0),{\vec {e}}_{2}=(0,1,0),{\vec {e}}_{3}=(0,0,1)} 时，向量和计算为

并且有如下的不等关系：

此外，向量的加法也满换律和结合律。

向量与积

向量空间分为有限维向量空间与无限维向量空间。在有限维向量空间中，可以找到一组（有限个）向量 e → → --> 1 , e → → --> 2 , ⋯ ⋯ --> , e → → --> n {\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},\cdots ,{\vec {e}}_{n}} ，使得任意一个向量 v → → --> {\displaystyle {\vec {v}}} 都可以唯一地表示成这组向量的线性组合：

其中的标量 v 1 , v 2 , ⋯ ⋯ --> , v n {\displaystyle v_{1},v_{2},\cdots ,v_{n}} 是随着向量 v → → --> {\displaystyle {\vec {v}}} 而确定的。这样的一组向量称为向量空间的基。给定了向量空间以及一组基后，每个向量就可以用一个数组来表示了。两个向量 v → → --> {\displaystyle {\vec {v}}} 和 w → → --> {\displaystyle {\vec {w}}} 相同，当且仅当表示它们的数组一样。

两个向量 v → → --> {\displaystyle {\vec {v}}} 和 w → → --> {\displaystyle {\vec {w}}} 的和：

它们的数量积为：

而标量k与向量v的乘积则为：

标量乘法

一个标量k和一个向量 v → → --> {\displaystyle {\vec {v}}} 之间可以做乘法，得出的结果是另一个与 v → → --> {\displaystyle {\vec {v}}} 方向相同或相反，大小为 v → → --> {\displaystyle {\vec {v}}} 的大小的｜k｜倍的向量，可以记成 k v → → --> {\displaystyle k{\vec {v}}} 。-1乘以任意向量会得到它的反向量，0乘以任何向量都会得到零向量 0 → → --> {\displaystyle {\vec {0}}} 。

两点向量与单点分量

向量的模长

向量的大小也叫做范数或者模长，有限维空间中，已知向量的坐标，就可以知道它的模长。设向量 v → → --> = ( v 1 , v 2 , ⋯ ⋯ --> , v n ) {\displaystyle {\vec {v}}=(v_{1},v_{2},\cdots ,v_{n})} ，

范数记作： ∥ v → → --> ∥ {\displaystyle \left\|{\vec {v}}\right\|} 模长记作： | v → → --> | {\displaystyle \left|{\vec {v}}\right|}

计算表达式由弗罗贝尼乌斯范数（一种同时适用于向量和矩阵的范数计算方法）给出： ∥ v → → --> ∥ = v 1 2 + v 2 2 + ⋯ ⋯ --> + v n 2 {\displaystyle \left\|{\vec {v}}\right\|={\sqrt {v_{1}^{2}+v_{2}^{2}+\cdots +v_{n}^{2}}}} 或： | v → → --> | = v 1 2 + v 2 2 + ⋯ ⋯ --> + v n 2 {\displaystyle \left|{\vec {v}}\right|={\sqrt {v_{1}^{2}+v_{2}^{2}+\cdots +v_{n}^{2}}}}

向量与定比分点、中点公式

在实际应用中，向量运算时常会运用到定比分点定理。

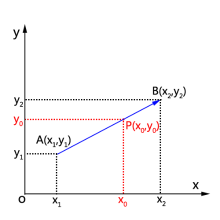
  平面直角坐标系Oxy

设平面直角坐标系 O x y {\displaystyle Oxy} 原点 O ( 0 , 0 ) {\displaystyle O(0,0)} ，内有点 A ( x 1 , y 1 ) {\displaystyle A(x_{1},y_{1})} ，点 B ( x 2 , y 2 ) {\displaystyle B(x_{2},y_{2})} ，点 P ( x 0 , y 0 ) {\displaystyle P(x_{0},y_{0})} ，点 P {\displaystyle P} 在点 A {\displaystyle A} 、 B {\displaystyle B} 之间，且

| A P → → --> | : | P B → → --> | = n {\displaystyle \left|{\overrightarrow {AP}}\right|:\left|{\overrightarrow {PB}}\right|=n} ，则：

O P → → --> ( x 1 + n x 2 1 + n , y 1 + n y 2 1 + n ) {\displaystyle {\overrightarrow {OP}}\left({\frac {x_{1}+nx_{2}}{1+n}},{\frac {y_{1}+ny_{2}}{1+n}}\right)}  

特殊地，当 n = 1 {\displaystyle n=1} ，

O P → → --> = ( x 1 + x 2 2 , y 1 + y 2 2 ) {\displaystyle {\overrightarrow {OP}}=\left({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}}\right)}

相应的有中点 P {\displaystyle P} 坐标： ( x 1 + x 2 2 , y 1 + y 2 2 ) {\displaystyle \left({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}}\right)}

实际上，上述结论可以推广到空间向量中。 设空间直角坐标系 O x y z {\displaystyle Oxyz} 内原点为 O ( 0 , 0 , 0 ) {\displaystyle O(0,0,0)} ，有点 A ( x 1 , y 1 , z 1 ) {\displaystyle A(x_{1},y_{1},z_{1})} ， B ( x 2 , y 2 , z 2 ) {\displaystyle B(x_{2},y_{2},z_{2})} ， A {\displaystyle A} 、 B {\displaystyle B} 点间有一点 P {\displaystyle P} ，且

| A P → → --> | : | P B → → --> | = n {\displaystyle \left|{\overrightarrow {AP}}\right|:\left|{\overrightarrow {PB}}\right|=n} ，

则： O P → → --> = ( x 1 + n x 2 1 + n , y 1 + n y 2 1 + n , z 1 + n z 2 1 + n ) {\displaystyle {\overrightarrow {OP}}=\left({\frac {x_{1}+nx_{2}}{1+n}},{\frac {y_{1}+ny_{2}}{1+n}},{\frac {z_{1}+nz_{2}}{1+n}}\right)}

中点 P {\displaystyle P} 坐标：

( x 1 + x 2 2 , y 1 + y 2 2 , z 1 + z 2 2 ) {\displaystyle \left({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}},{\frac {z_{1}+z_{2}}{2}}\right)}  

附：平面几何中定比分点定理的证明

设平面直角坐标系 O x y {\displaystyle Oxy} 内原点 O ( 0 , 0 ) {\displaystyle O(0,0)} ，有点 A ( x 1 , y 1 ) {\displaystyle A(x_{1},y_{1})} ，点 B ( x 2 , y 2 ) {\displaystyle B(x_{2},y_{2})} ，点 P ( x 0 , y 0 ) {\displaystyle P(x_{0},y_{0})} ，点 P {\displaystyle P} 在点 A {\displaystyle A} 、 B {\displaystyle B} 之间，且 | A P | : | P B | = n {\displaystyle \left|AP\right|:\left|PB\right|=n} ，则：

x 0 − − --> x 1 x 2 − − --> x 0 = n ⇒ ⇒ --> x 0 = x 1 + n x 2 1 + n {\displaystyle {\frac {x_{0}-x_{1}}{x_{2}-x_{0}}}=n\Rightarrow x_{0}={\frac {x_{1}+nx_{2}}{1+n}}} ，y 0 − − --> y 1 y 2 − − --> y 0 = n ⇒ ⇒ --> y 0 = y 1 + n y 2 1 + n {\displaystyle {\frac {y_{0}-y_{1}}{y_{2}-y_{0}}}=n\Rightarrow y_{0}={\frac {y_{1}+ny_{2}}{1+n}}}

参见

向量空间

向量分析

向量场

标量

张量

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。