磁场
定义
按照磁场对于周围环境的影响,可以用几种等价的方法来定义磁场。例如,类似于电场,磁场对电荷会施加作用力;但与电场不同的是,它只对移动中的电荷施加作用力,而且作用力的方向垂直于磁场本身和电荷速度。这作用力称为洛伦兹力,以方程表示,
其中,
另外一种对于磁场的工作定义是由处于磁场的磁偶极子所感受到的力矩给出,以方程表示,
其中,
历史
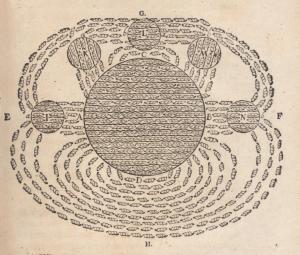
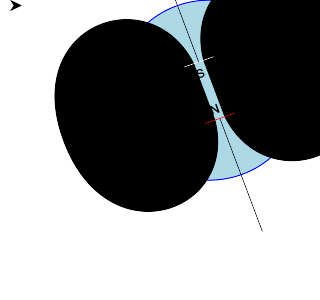
最早出现的几副磁场绘图之一,绘者为勒内·笛卡儿,1644年。这绘图显示出地球(中心大圆球)的磁场吸引几块圆形磁石(以I、K、L、M、N标记的圆球)。笛卡儿认为磁性是由微小螺旋状粒子的环流造成的,称为“螺纹子”。这些螺纹子穿过磁铁的平行螺纹细孔,从指南极(A)进入,从指北极(B)出来,经过磁铁外的空间(G、H)再绕回指南极。当螺纹子绕动至磁石附近时,会穿过其细孔,从而造成磁力。
虽然很早以前,人类就已知道磁石和其奥妙的磁性,最早出现的几个学术性论述之一,是由法国学者皮埃·德马立克( Pierre de Maricourt )于公元1269年写成 。德马立克仔细标明了铁针在块型磁石附近各个位置的定向,从这些记号,又描绘出很多条磁场线。他发现这些磁场线相会于磁石的相反两端位置,就好像地球的经线相会于南极与北极。因此,他称这两位置为 磁极 。几乎三个世纪后,威廉·吉尔伯特主张地球本身就是一个大磁石,其两个磁极分别位于南极与北极。出版于1600年,吉尔伯特的巨著《论磁石》( De Magnete )开创磁学为一门正统科学学术领域。
于1824年,西莫恩·泊松发展出一种物理模型,比较能够描述磁场。泊松认为磁性是由磁荷产生的,同类磁荷相排斥,异类磁荷相吸引。他的模型完全类比现代静电模型;磁荷产生磁场,就如同电荷产生电场一般。这理论甚至能够正确地预测储存于磁场的能量 。
尽管泊松模型有其成功之处 ,这模型也有两点严峻瑕疵。第一,磁荷并不存在。将磁铁切为两半,并不会造成两个分离的磁极,所得到的两个分离的磁铁,每一个都有自己的指南极和指北极。第二,这模型不能解释电场与磁场之间的奇异关系。
于1820年,一系列的革命性发现,促使开启了现代磁学理论。首先,丹麦物理学家汉斯·奥斯特于7月发现载流导线的电流会施加作用力于磁针,使磁针偏转指向。稍后,于9月,在这新闻抵达法国科学院仅仅一周之后,安德烈-玛丽·安培成功地做实验展示出,假若所载电流的流向相同,则两条平行的载流导线会互相吸引;否则,假若流向相反,则会互相排斥。紧接着,法国物理学家让-巴蒂斯特·毕奥和菲利克斯·沙伐于10月共同发表了毕奥-萨伐尔定律;这定律能够正确地计算出在载流导线四周的磁场。
1825年,安培又发表了安培定律。这定律也能够描述载流导线产生的磁场。更重要的,这定律帮助建立整个电磁理论的基础。于1831年,麦可·法拉第证实,随着时间而变化的磁场会生成电场。这实验结果展示出电与磁之间更密切的关系。
从1861年到1865之间,詹姆斯·麦克斯韦将经典电学和磁学杂乱无章的方程加以整合,发展成功麦克斯韦方程组。最先发表于他的1861年论文《论物理力线》,这方程组能够解释经典电学和磁学的各种现象。在论文里,他提出了“分子涡流模型”,并成功地将安培定律加以延伸,增加入了一个有关于位移电流的项目,称为“麦克斯韦修正项”。由于分子涡包具有弹性,这模型可以描述电磁波的物理行为。因此,麦克斯韦推导出电磁波方程。他又计算出电磁波的传播速度,发现这数值与光速非常接近。警觉的麦克斯韦立刻断定光波就是一种电磁波。后来,于1887年,海因里希·赫兹做实验证明了这事实。麦克斯韦统一了电学、磁学、光学理论。
虽然,有了极具功能的麦克斯韦方程组,经典电动力学基本上已经完备,在理论方面,二十世纪带来了更多的改良与延伸。阿尔伯特·爱因斯坦,于1905年,在他的论文里表明,电场和磁场是处于不同参考系的观察者所观察到的同样现象(帮助爱因斯坦发展出狭义相对论的思想实验,关于其详尽细节,请参阅移动中的磁铁与导体问题)。后来,电动力学又与量子力学合并为量子电动力学。
B场与H场
在各个学术领域里,磁场会被用来称呼两种不同的矢量场,分别标记为 H {\displaystyle \mathbf {H} } 和 B {\displaystyle \mathbf {B} } 。矢量场 H {\displaystyle \mathbf {H} } 又时常称为“磁场强度”(magnetic field intensity或magnetic field strength)或“附属磁场”( auxilliary magnetic field )或干脆“H场” 。矢量场 B {\displaystyle \mathbf {B} } 也时常称为“磁通量密度”(magnetic flux density)、“磁感应强度”(magnetic induction)、“B场”。
虽然“磁场”这个词汇在历史上已先被H场占有,而只能将B场称为“磁感应”,但是现在多数物理学家公认B场为更基本的物理量,因此他们称呼B场为“磁场” 。如同命名表格展示,B场和H场的习惯命名并不一致。为了分歧义,在本文章里,磁感应强度指的是B场,磁场强度指的是H场,而磁场则依上下文而定,通常指的是B场。
H场以方程定义为
其中, μ μ --> 0 {\displaystyle \mu _{0}} 是磁常数, M {\displaystyle \mathbf {M} } 是磁化强度。
对于线性物质,磁化强度 M {\displaystyle \mathbf {M} } 与B场成正比,所以,B场与H场之间的关系为
其中, μ μ --> ′ {\displaystyle \mu "} 是磁导率。
在自由空间里,磁化强度等于零,所以,
对于很多其它物质,磁化强度与B场之间的关系相当复杂。例如,铁磁性物质和超导体的磁化强度是 B {\displaystyle \mathbf {B} } 的多值函数( multivalued function )。这现象称为迟滞现象 。
在国际单位制里,B场的单位为特斯拉(tesla),等价于韦伯(weber)/平方米,或伏特·秒/平方米。在CGS单位制里,B场的单位为高斯(gauss)。1特斯拉等于10,000高斯。在国际单位制里,H场的单位为安培/米;在CGS单位制里,H场的单位为奥斯特(oersted)。1奥斯特定义为 1000 / 4 π π --> ≈ ≈ --> 79.5774715 {\displaystyle 1000/4\pi \approx 79.5774715} 安培/米 。
精密仪器能够测量到的最微小磁场的数量级为阿托特斯拉(10 特斯拉) ;实验室能够制备的最强烈磁场为2800特斯拉 。很多像磁星一类的天文星体,其磁场值域为0.1至100吉咖特斯拉(10 至10 特斯拉),超强于最强烈的实验室磁场 。
磁强计( magnetometer )是测量局域磁场的仪器。磁强计又分为很多类,重要的几类包括霍尔效应磁强计、超导磁强计、核子旋进磁力仪( NMR magnetometer )、磁通门磁强计( fluxgate magnetometer )等等。遥远的天文星体的磁场可以靠着测量其对于附近带电粒子的影响而得知。例如,绕着磁场线螺旋转动的电子会产生同步辐射,其无线电波数据可以用电波望远镜侦测获得。
磁场线
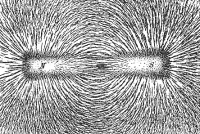
透过铁粉显示出的磁场线。
磁场的方向可以借着磁偶极子的性质来显示,处于磁场的磁偶极子会沿着磁场的磁场线平行排列,其中的一个显著例子就是磁铁周围的铁粉分布图案。将条状磁铁放在白纸下面,铺洒一堆铁粉在白纸上面,这些铁粉会依著正切磁场线的方向排列,形成一条条曲线,在曲线的每一点显示出磁场线的正切方向。这曲线图称为“场线图”。
绘制场线图是一种很简单的、描述磁场(或任意其它矢量场)的方法,在空间的任意位置的磁场可以从场线图在对应位置的场线正切方向和密度估计出来。磁场线密度越高表示磁场越强劲。场线图的绘制相当容易。首先,在每一个位置测量磁场的数值大小和方向。按照所得数据,在图纸的对应位置绘出一条跟磁场同方向的箭杆。然后,将每条箭杆之首部与前面的箭杆之尾部连接起来,形成磁场线,确使磁场线密度与磁场的强度成正比。这样,就可以绘制出一幅场线图。这是一种很优良的磁场视觉化方法。想像磁场线会沿着线径施加张力(像一条橡皮圈),又会垂直于线径对邻近的磁场线施加压力,这就是磁力的物理行为。两块磁铁的异性磁极互相吸引,这是由于它们被很多条磁场线连结;反之,两块磁铁的同性磁极互相排斥,这是由于它们的磁场线不相交接,因为互相平行,造成互相推挤。
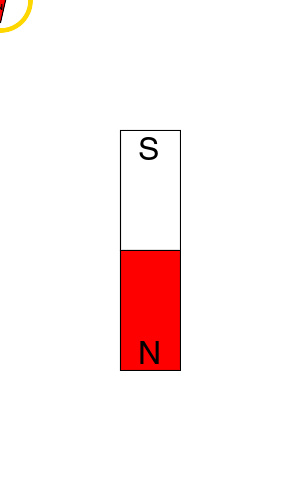
指南针显示出一个条形磁铁的磁场方向。指南针的指北极(红色)会被磁铁的指南极(S极)吸引,也会被磁铁的指北极(N极)排斥。
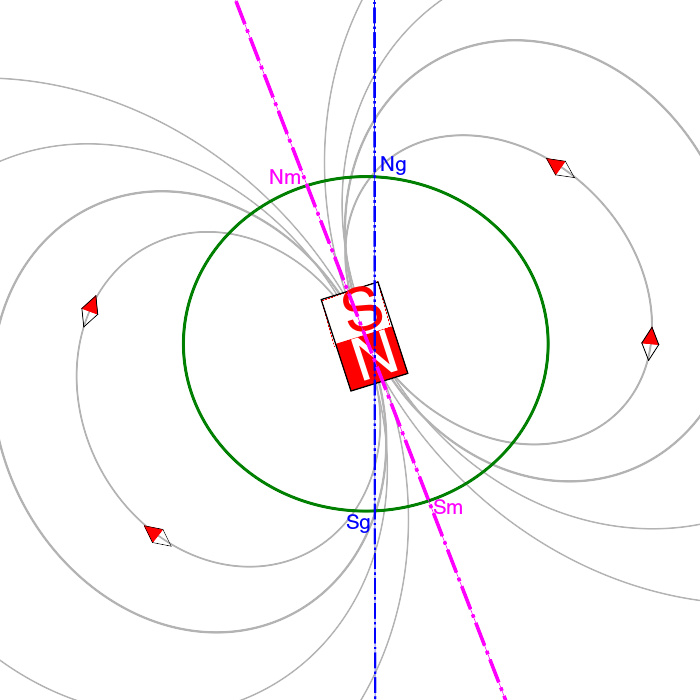
磁场在任意位置的方向可以用指南针来显示。指南针可以显示出一个条形磁铁的磁场方向。由于异性磁极相互吸引,指南针的指北极会被磁铁的指南极(S极)吸引;由于同性磁极相互排斥,指南针的指北极会被磁铁的指北极(N极)排斥。在磁铁的指南极附近,磁场指向磁铁;在指北极附近,磁场背向磁铁。载流导线产生的磁场不会指向导线,也不会背向导线,而会环绕着导线。
出现于地球北极高空或南极高空的极光也可以显示出磁场线。从太阳流出来的大量离子形成了太阳风,其中一部分会流往地球,在地球高空,被地球磁场捕获,沿着磁场线集中至北极高空与南极高空。这些离子跟大气层的原子、分子之间的碰撞,造成了能量以极光形式被释出。通常,极光看起来像是漫射( diffusion )的辉光( glow )或“光帘”,朝着东-西方向延伸。每一张光帘是由许多条平行射线组成。每一条射线与在那位置的磁场线同方向。这令人觉得极光是由地球的磁场塑造成形的。确实无误,从人造卫星的观察证实了离子被磁场线引导,一边绕着磁场线盘旋,一边朝着地球移动。
B场线永不终结
绘制场线图是一种很有用的表示矢量场的方法,可以很简单地显示出矢量场的细致属性。磁场的一个很重要的性质可以用场线图显示出来:磁场线没有初始点,也没有终结点;磁场线会形成闭回路,或从无穷远延伸至无穷远。至今,科学家尚未发现任何例外。磁场是一种螺线矢量场。
磁场线会从磁铁的指北极附近离开磁铁,又会从磁铁的指南极附近进入磁铁;在磁铁内部,磁场线仍旧从指南极连结至指北极 。任何一条进入磁铁的磁场线必定会从磁铁出来;绝不容许磁场线终结于任何位置。磁极总是以指北极和指南极一对一对的形式出现。将磁铁切为两半,会形成两块磁铁,其中每一块磁铁都拥有自己的指北极和指南极。
更正式而言,所有进入某区域的磁场线,也必须离开那区域。因此,进入某区域的磁场线的数目 ,减去离开那区域的磁场线的数目,结果必须等于零。这结果称为高斯磁定律,以方程表示:
其中, S {\displaystyle \mathbb {S} } 是闭曲面, d a {\displaystyle \mathrm {d} \mathbf {a} } 是微小面元素。
H场线开始与终结于磁极
在磁性物质外面,H场线与B场线等同;但在磁性物质内部,H场与B场的数值大小、方向可能不同,这依赖磁化强度 M {\displaystyle \mathbf {M} } 而定,这关系可以由H场的定义方程看出来:
假设外磁场等于零,则在一个均匀磁铁内部,B场与H场呈相反方向。H场线开始于指北极,终结于指南极。相与比较,B场线形成一个闭循环,在磁铁内部,从指南极延续到指北极,在磁铁外部,又从指北极绕道至指南极。H场线与电场线类似;电场线开始于正电荷,终结于负电荷。这使人想要以处于两端局域的磁荷为磁铁的模型。很可惜地,这磁荷模型并不正确,尤其是当计算磁铁内部的磁场时。
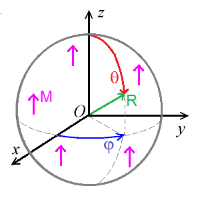
一个磁化强度为 M = M z ^ ^ --> {\displaystyle \mathbf {M} =M{\hat {z}}} 的均匀磁性球体。
例如,参阅右图,采用原子尺寸载流循环模型来描述,一个磁化强度为 M = M z ^ ^ --> {\displaystyle \mathbf {M} =M{\hat {z}}} 均匀磁性球体,等价于一个满足以下条件的球体:内部的束缚电流密度 J b {\displaystyle J_{b}} 和表面束缚电流密度 K b {\displaystyle K_{b}} 分别为
其中, n ^ ^ --> {\displaystyle {\hat {n}}} 是垂直于球体表面的径向单位矢量。
经过一番运算,可以得到,表面束缚电流密度为 M sin --> θ θ --> {\displaystyle M\sin \theta } 的球体,其内部B场为
从H场 H {\displaystyle \mathbf {H} } 的定义式,
所以,在均匀磁化球体内部,B场与H场呈相反方向 。
磁单极子
磁单极子是一种假想的粒子(或粒子类),这粒子只拥有一个磁极(指北极或指南极)。换句话说,类似带电粒子的拥有电荷,磁单极子拥有磁荷。
现今,对于这概念的兴趣大多出自于粒子物理学,特别值得注意的是大统一理论和超弦理论,关于磁单极子的存在或可能性,它们做了很多预测,因而激发出许多物理学者寻找磁单极子的强烈兴趣。但尽管竭尽全力,物理学者至今仍旧无法观察到任何磁单极子的蛛丝马迹
最新进研究发现自旋冰( spin ice )是一种可以模拟磁单极子的材料,但不含有真实的磁单极子。
磁偶极子
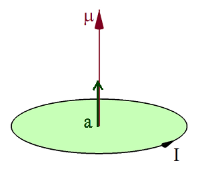
假设一个平面载流循环的面积矢量为 a {\displaystyle \mathbf {a} } 、所载电流为 I {\displaystyle I} ,则其磁偶极矩为 μ μ --> = I a {\displaystyle {\boldsymbol {\mu }}=I\mathbf {a} } 。
假设一个平面载流循环的面积矢量为 a {\displaystyle \mathbf {a} } 、所载电流为 I {\displaystyle I} ,则其磁偶极矩 μ μ --> {\displaystyle {\boldsymbol {\mu }}} 的方向,根据右手法则,是大拇指从载流循环的平面指出的方向,而其它拇指的指向则与电流的流动方向相同,磁偶极矩的大小等于电流乘以循环的面积。以方程表示,磁偶极矩 μ μ --> {\displaystyle {\boldsymbol {\mu }}} 为
这有限面积的载流循环还有更高阶的磁矩,像磁四极矩,磁八极矩等等。假设载流循环的面积趋向于零、电流趋向于无穷大,同时保持 μ μ --> = I a {\displaystyle {\boldsymbol {\mu }}=I\mathbf {a} } 不变,则所有更高阶的磁矩会趋向于零,这真实的载流循环趋向于一个理想磁偶极子,或纯磁偶极子。这模型称为 电流模型 。采用这模型,可以很容易地找到角动量与磁矩之间的关系。爱因斯坦-德哈斯效应,由磁化而产生的旋转现象,和其逆反,巴尼特效应( Barnett effect ),由旋转而产生的磁化现象,这两种效应基本是在展示角动量与磁矩之间的关系。应用巴尼特效应,将载流循环顺着电流方向旋转,会使电流增大,连带地也增大了磁矩。
磁偶极子的磁场
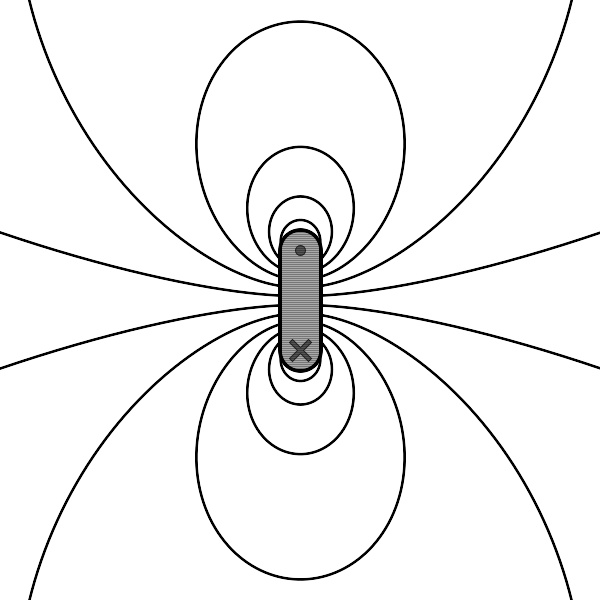
一个指向右方的磁偶极子的磁场线。
假设磁偶极矩为 μ μ --> {\displaystyle {\boldsymbol {\mu }}} 的磁偶极子,其位原点在原点,则在任意位置 r {\displaystyle \mathbf {r} } ,磁偶极子的矢势 A {\displaystyle \mathbf {A} } 是
其中, μ μ --> 0 {\displaystyle \mu _{0}} 是磁常数。
这磁偶极子所产生的磁场 B {\displaystyle \mathbf {B} } 为
由于磁偶极子的矢势有一个奇点在它所处的位置(原点 O {\displaystyle \mathbf {O} } ),必须特别小心地计算,才能得到正确答案。更仔细地推导,可以得到磁场为
任意磁场的多极展开式中,带头项目就是这公式右手边的第一个项目,偶极子项目。磁场没有单极子项目。在远距离,这公式近似任何类似磁偶极子的组态所产生的磁场。
磁偶极子感受到的磁力矩
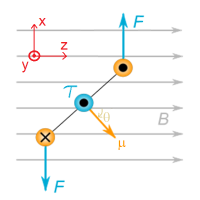
处于均匀磁场的一个方形载流循环。
如图右,假设载有电流 I {\displaystyle I} 的一个方形循环处于外磁场 B = B 0 z ^ ^ --> {\displaystyle \mathbf {B} =B_{0}{\hat {\mathbf {z} }}} 。方形循环四个边的边长为 w {\displaystyle w} ,其中两个与 y ^ ^ --> {\displaystyle {\hat {\mathbf {y} }}} 平行的边垂直于外磁场,另外两个边与磁场之间的夹角角弧为 − − --> θ θ --> + π π --> / 2 {\displaystyle -\theta +\pi /2} 。
垂直于外磁场的两个边所感受的磁力矩为
另外两个边所感受的磁力矩互相抵消。注意到这循环的磁偶极矩为 μ μ --> = I w 2 μ μ --> ^ ^ --> {\displaystyle {\boldsymbol {\mu }}=Iw^{2}{\hat {\boldsymbol {\mu }}}} 。所以,这循环感受到的磁力矩为
令载流循环的面积趋向于零、电流趋向于无穷大,同时保持 μ μ --> = I a {\displaystyle {\boldsymbol {\mu }}=I\mathbf {a} } 不变,则这载流循环趋向于理想磁偶极子。所以,处于外磁场的磁偶极子所感受到的磁力矩也可以用上述方程表示。
当磁偶极矩垂直于磁场时,磁力矩的大小是最大值 μ μ --> B 0 {\displaystyle \mu B_{0}} ;当磁偶极矩与磁场同线时,磁力矩等于零。
磁偶极子的势能
将载流循环从角弧 θ θ --> 1 {\displaystyle \theta _{1}} 扭转到角弧 θ θ --> 2 {\displaystyle \theta _{2}} ,磁场所做的机械功 W {\displaystyle W} 为
注意到磁力矩的扭转方向是反时针方向,而 θ θ --> {\displaystyle \theta } 是朝着顺时针方向递增,所以必须添加一个负号。设定 θ θ --> 1 = π π --> / 2 {\displaystyle \theta _{1}=\pi /2} ,则
对抗这磁场的磁力矩,将载流循环从角弧 π π --> / 2 {\displaystyle \pi /2} 扭转到角弧 θ θ --> 2 {\displaystyle \theta _{2}} ,所做的机械功 W a {\displaystyle W_{a}} 为
定义载流循环的势能 U {\displaystyle U} 等于这机械功 W a {\displaystyle W_{a}} ,以方程表示为
这也是磁偶极子的势能。当磁矩垂直于磁场时,势能等于零;当磁矩与磁场呈相同方向时,势能是最小值 − − --> μ μ --> B 0 {\displaystyle -\mu B_{0}} ;当磁矩与磁场呈相反方向时,势能是最大值 μ μ --> B 0 {\displaystyle \mu B_{0}} 。
永久磁铁
永久磁铁会在周围产生持续不变的磁场。永久磁铁大多是由像铁或镍一类的铁磁性物质经过磁化而制成。每一个永久磁铁都具有磁矩,其方向是从磁铁的指南极指向指北极。指南极和指北极分别位于条形磁铁的两端,称为“磁极”。
永久磁铁的磁场
永久磁铁的磁场比较复杂,特别是在磁铁附近。一个微小条形磁铁 的磁场与其磁矩成正比,也会与磁铁的定向有关。当尺寸驱向无穷小极限时,磁铁可以理想化成为磁偶极子,以方程表示,这微小条形磁铁(磁偶极子)产生的磁场为
其中, r {\displaystyle \mathbf {r} } 是从磁铁位置至场位置的位移矢量,其单位矢量是 r ^ ^ --> {\displaystyle {\hat {\mathbf {r} }}} ,其距离是 r {\displaystyle r} , μ μ --> 0 {\displaystyle \mu _{0}} 是磁常数, μ μ --> {\displaystyle {\boldsymbol {\mu }}} 是微小磁铁的磁矩。
有时候,磁铁与磁铁之间感受到的磁力和力矩,可以采用“磁极模型”来计算,磁极与磁极之间会互相吸引或互相排斥,就好像电荷与电荷之间的库伦力。很可惜地,磁极模型不能正确地反映出磁铁内部的真实状况(请参阅铁磁性)。科学家尚未找到磁荷存在的实证。磁铁的指北极与指南极无法被分离;任何分离动作会造成两个子磁铁,各自拥有自己的指北极与指南极。磁极模型无法解释电流产生的磁场,也无法解释移动于磁场中的电荷所感受到的洛伦兹力。
更正确地描述磁性,涉及了计算广泛分布于磁铁内部的原子尺寸载流循环所产生的磁场 。
外磁场作用于磁铁的力矩
处于外磁场的磁铁会感受到外磁场施加的力矩,促使磁铁的磁矩与外磁场呈相同方向。做简单实验就可以很容易地观察到这现象:固定一块条形磁铁X于某位置,假若磁铁X作用于条形磁铁Y的磁场与磁铁Y的磁矩呈不同方向,则会有力矩作用于磁铁Y,促使磁铁Y旋转,使得磁铁Y的磁矩与磁铁X的磁场呈相同方向。磁矩为 μ μ --> {\displaystyle {\boldsymbol {\mu }}} 的磁铁Y,因为处于磁铁X所产生的磁场 B {\displaystyle \mathbf {B} } ,而感受到的力矩 τ τ --> {\displaystyle {\boldsymbol {\tau }}} 以方程表示为
这现象可以解释,为什么在地球表面某位置的局域磁场方向,是指南针(或任意磁铁)的指北极的指向。
磁场与磁矩耦合产生的力矩可以用来驱动简单的电动机。在一个简单的直流电动机设计图里,固定一块磁铁于自由旋转的旋转轴(称为转子),排列一组电磁铁(称为定子)于旋转轴的外周。然后,开启交流电通过每一块电磁铁,每一股电流与隔邻的电流,其相位差是有限常定值。这样,在旋转轴位置,会造成旋转磁场。感受到磁场施加的力矩,转子的磁矩会趋于与磁场呈相同方向,因此,转子会跟着旋转磁场不停地旋转。这就是电动机将电能转换为机械能的基本运作机制。
假若逆反上述机制,则可将机械能转换为电能。这是发电机的运作机制。
在后面旋转磁场段落里,还有更多有关这种使用电磁铁的例子。
外磁场作用于磁铁的磁力
高磁场区域会吸引或排斥磁铁,决定于磁铁与磁场之间的相对取向。这是个一般定则。异性磁极相互吸引,同性磁极相互排斥,就是这定则的特例。两个磁铁的异性磁极相互吸引,因为两个异性磁极之间的磁场较强烈,而且这磁场与磁铁的磁矩呈相同方向。
假设磁矩的方向被逆反,则结果也会被逆反。假设磁铁的磁矩与磁场呈相反方向,而磁铁又不会因为磁场施加的力矩而改变取向,则作用于磁铁的磁力,其方向会朝向磁场比较微弱的区域,这对应于两个磁铁的同性磁极相互排斥。不均匀外磁场可以区分不同定向的磁偶极子,这是著名的施特恩-格拉赫实验的运作原理。这实验建立了原子及电子的磁偶极矩的量子性质 。
处于不均匀外磁场 B {\displaystyle \mathbf {B} } 的磁铁所感受到的磁力 F {\displaystyle \mathbf {F} } ,以方程近似为
其中, μ μ --> {\displaystyle {\boldsymbol {\mu }}} 是磁铁的磁矩。
注意到 − − --> μ μ --> ⋅ ⋅ --> B {\displaystyle -{\boldsymbol {\mu }}\cdot \mathbf {B} } 是磁场与磁矩之间的作用能量。所以,作用力 F {\displaystyle \mathbf {F} } 的方向是朝向减少作用能量的方向。磁矩 μ μ --> {\displaystyle {\boldsymbol {\mu }}} 固定不变,当磁场与磁矩呈相同方向时,作用力的方向是朝向磁场比较强的区域;当磁场与磁矩呈相反方向时,作用力的方向是朝向磁场比较弱的区域。这方程对于零尺寸的磁铁(磁偶极子)完全正确;对于其它小尺寸的磁铁则是近似正确;对于大尺寸磁铁,必须将其分为几个小区域,再将每一个小区域的磁矩所感受到的磁力综合为总磁力。
电流与磁场
电流会产生磁场。这电流可以是在导线内的巨观电流,或是运动于原子轨域的电子所形成的微观电流。处于外磁场的载流导线会感受到外磁场施加的磁力。
运动中的带电粒子所生成的磁场
所有运动中的带电粒子都会生成相当复杂、但众所熟悉的磁场 。这磁场与粒子的带电量、速度和加速度有关。
由于带电粒子的运动不能形成电流,所以,必须应用推迟势概念来计算其电场和磁场。假设一个带有电量 q {\displaystyle q} 的粒子以等速度 v {\displaystyle \mathbf {v} } 移动,在时间 t {\displaystyle t} 的位置为 w = v t {\displaystyle \mathbf {w} =\mathbf {v} t} 。那么,麦克斯韦方程组给出此带电粒子所生成在场位置为 r {\displaystyle \mathbf {r} } 的电场和磁场:
其中, ϵ ϵ --> 0 {\displaystyle \epsilon _{0}} 是电常数, c {\displaystyle c} 是光速, r {\displaystyle \mathbf {r} } 是场位置, θ θ --> {\displaystyle \theta } 是 v {\displaystyle \mathbf {v} } 和 r − − --> w {\displaystyle \mathbf {r} -\mathbf {w} } 之间的夹角。
这方程最先由奥利弗·亥维赛于1888年推导出来。当 v 2 ≪ ≪ --> c 2 {\displaystyle v^{2}\ll c^{2}} 时,电场和磁场可以近似为
电场的方程就是库仑定律,磁场的方程称为“毕奥-沙伐点电荷定律” 。
电流产生的磁场
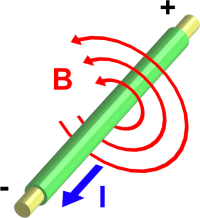
载流导线的电流 I {\displaystyle I} 在周围产生磁场 B {\displaystyle \mathbf {B} } 。磁场的方向可以用右手定则找出。

螺线管绘图。
磁场线以同心圆图样环绕着载流导线。磁场的方向可以用右手定则找出,其大小与离载流导线的径向距离呈平方反比。毕奥-萨伐尔定律阐明,假设源位置为 r ′ {\displaystyle \mathbf {r} "} 的微小线元素 d ℓ ℓ --> ′ ′ --> {\displaystyle \mathrm {d} {\boldsymbol {\ell }}^{\ \prime }} 载有电流 I {\displaystyle I} ,则 d ℓ ℓ --> ′ ′ --> {\displaystyle \mathrm {d} {\boldsymbol {\ell }}^{\ \prime }} 贡献出的磁场 d B {\displaystyle \mathrm {d} \mathbf {B} } 在场位置 r {\displaystyle \mathbf {r} } 为
采用静磁近似,当电流足够缓慢地随时间而改变时(例如当载流导线足够缓慢地移动时),这定律成立。
将一根载流导线弯卷成为线圈。这动作会增强线圈内部的磁场,同时减弱线圈外部的磁场。将导线多重卷绕为紧密的多匝线圈,会增强这效应。这多匝线圈,称为螺线管。在螺线管内加入铁芯,会更加增强这效应,整个物体称为电磁铁,可以产生强大的,能被准确控制的磁场。长度超大于直径的电磁铁,可以近似其内部磁场为均匀磁场,近似其外部磁场为零。
在静磁学里,安培定律描述磁场与电流之间的关系。其积分形式与微分形式分别为
其中, C {\displaystyle \mathbb {C} } 是路径积分的闭回路, I e n c {\displaystyle I_{\mathrm {enc} }} 是闭回路 C {\displaystyle \mathbb {C} } 所围住的电流, J {\displaystyle \mathbf {J} } 是电流密度。
对于稳定电流,安培定律恒成立。对于计算具有高度对称性的案例,像无穷长导线或无穷长螺线管,安培定律特别有用。
假设电场含时间,则安培定律不正确,必需加以修正。将麦克斯韦修正项目加入安培定律的方程,成为麦克斯韦-安培方程:
其中, D {\displaystyle \mathbf {D} } 是电势移。
这是麦克斯韦方程组的四条方程中之一条。
电流与磁力
移动中的带电粒子所感受到的磁力
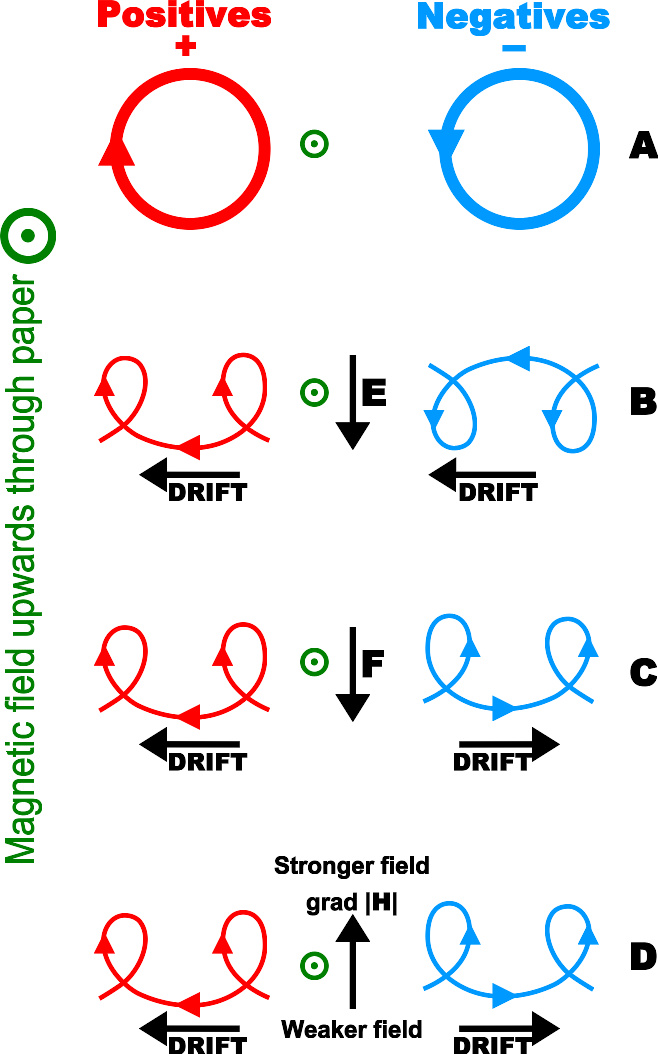
带电粒子漂移(DRIFT)于均匀磁场中的轨迹 。(A)没有其它作用力干扰(B)添加电场 E {\displaystyle \mathbf {E} } (C)添加恒力 F {\displaystyle \mathbf {F} } (例如:引力,(D)改为不均匀的磁场, ∇ ∇ --> | H | ≠ ≠ --> 0 {\displaystyle \nabla |H|\neq 0}
移动于磁场中的带电粒子会感受到洛伦兹力。其大小与磁场,粒子的带电量、粒子垂直于磁场的移动速度成正比,以方程表示,
其中, F {\displaystyle \mathbf {F} } 是洛伦兹力, q {\displaystyle q} 是粒子的带电量, v {\displaystyle \mathbf {v} } 是粒子的移动速度。
洛伦兹力必定垂直于 B {\displaystyle \mathbf {B} } 和 v {\displaystyle \mathbf {v} } 。固定不动的粒子或沿着磁场线移动的粒子都不会感受到任何洛伦兹力。带电粒子绕着磁场线移动的轨迹是圆形的(更一般地,由于带电粒子可能会沿着磁场线移动,轨迹是螺旋形的),这运动称为回旋运动( cyclotron motion )。由于磁力永远垂直于移动方向,磁场不能做任何机械功于孤独电荷。但是,磁场可以改变粒子的移动方向,甚至于使得感受到某外力作用的粒子会朝着垂直于那外力的方向漂移。时常,会有人士声称磁力可以做机械功于真实磁偶极子或束缚于某种作用力的带电粒子。但是这些皆属无稽之谈 。
载流导线所感受到的磁力
由于电流是一群移动中的带电粒子所形成的巨观效应,载流导线所感受到的磁力类似移动中的带电粒子所感受到的磁力。处于磁场中的载流导线会感受到一种侧向力。
假设电场为零,则作用于移动速度为 v {\displaystyle \mathbf {v} } 的电荷 q {\displaystyle q} 的洛伦兹力是
对于线电荷密度为 λ λ --> {\displaystyle \lambda } 的载流导线,总洛伦兹力为
其中, C {\displaystyle \mathbb {C} } 是积分路径, I = λ λ --> v {\displaystyle \mathbf {I} =\lambda \mathbf {v} } 是电流矢量。
假设电流是稳定电流,则可以将电流从积分内提出,用微小线元素矢量 d ℓ ℓ --> {\displaystyle \mathrm {d} {\boldsymbol {\ell }}} 来表示电流 I {\displaystyle \mathbf {I} } 的方向:
这公式给出了处于外磁场的载流导线所感受到的磁力。使用这公式和毕奥-萨伐尔定律,就可以推导出安培力定律(详尽细节,请参阅安培力定律)。
假设,磁场是均匀磁场,积分路径是垂直于磁场的直线,则
其中, L {\displaystyle L} 是积分路径 C {\displaystyle \mathbb {C} } 的长度。
磁力的方向
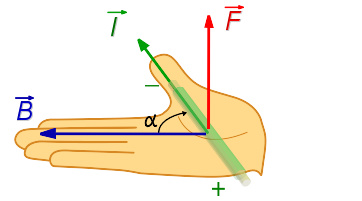
右手开掌定则 :使用右手,将大拇指朝着电流方向指去,再将其它四根手指朝着磁场方向指去,则掌心所面对的方向就是磁力的方向。
如左图所示,电流、磁场与导线受力方向,三者之间的关系,可用“右手开掌定则”来决定:“将右手掌张开,四指指向磁场方向,大拇指张开,与四指垂直,指向导线的电流方向,则掌心推出的方向即为导线的受力方向,三者间两两相互垂直”。
由于正电荷移动的方向相反于负电荷移动的方向,但都会形成同样方向的电流,只靠着测量产生的磁场,并不能分辨出到底是正电荷在移动还是负电荷在以相反方向移动。若要分辨出电荷载子的种类,必须施加外磁场,这外磁场垂直于电荷移动方向,使得电荷因感受到洛伦兹力而偏向一边,从测量两边之间的电压,可以侦测出到底是哪种电荷在移动。详尽细节,请参阅条目霍尔效应。
磁性物质内外的H场与B场
当计算磁场时,假若用总电流为参数,则前面推导出来的磁场方程正确无误。但是,处于外磁场的磁性物质会生成自己的束缚电流,计算这束缚电流可能颇费工夫。这束缚电流是由原子尺寸载流循环,与物质内部像电子一类的亚原子粒子的自旋,共同形成的。假若改计算先前定义的H场,则可避免计算束缚电流,但在学习这技巧之前,必须先了解磁化强度概念。
磁化强度
磁化强度 M {\displaystyle \mathbf {M} } 描述物质的磁化程度,定义为单位体积的磁偶极矩,以方程表示为
其中, n {\displaystyle n} 是磁偶极子密度, μ μ --> {\displaystyle {\boldsymbol {\mu }}} 是磁偶极子的磁偶极矩。
当施加外磁场于磁性物质时,磁性物质的内部会被磁化,会出现众多磁偶极子。磁化强度计量磁性物质被磁化的程度。采用国际单位制,磁化强度的单位是安培/米,方向是巨观的平均磁偶极矩的方向。一个均匀磁铁的磁化强度乘以体积,就可以得到这磁铁的磁矩。与B场不同,磁化强度只存在于磁性物质内部。因此,磁化强度场线开始与终结于磁极。
合乎物理理论的正确计算方法是,总和所有产生磁化强度的磁偶极子的电流,得到的电流称为 束缚电流 ,这是磁性物质用来产生磁场的源头。按照这方法,磁性物质内部的 束缚电流密度 J b {\displaystyle J_{b}} 和 表面束缚电流密度 K b {\displaystyle K_{b}} 分别为
其中, n ^ ^ --> {\displaystyle {\hat {n}}} 是垂直于磁性物质表面的单位矢量。
从这些束缚电流密度,可以计算出磁化强度所贡献的磁场。
H场与磁性物质
H场 H {\displaystyle \mathbf {H} } 定义为
使用H场 H {\displaystyle \mathbf {H} } 的优点是它与束缚源无关,只涉及自由源。例如,将 H {\displaystyle \mathbf {H} } 路径积分于闭回路 C {\displaystyle \mathbb {C} } ,会得到穿过闭回路 C {\displaystyle \mathbb {C} } 内部的净自由电流 I f {\displaystyle I_{\mathrm {f} }} (不包括束缚电流 I b {\displaystyle I_{\mathrm {b} }} ):
应用磁荷的概念,将 H {\displaystyle \mathbf {H} } 曲面积分于任意闭曲面 S {\displaystyle \mathbb {S} } ,会捕获所有在闭曲面 S {\displaystyle \mathbb {S} } 内的磁荷 q M {\displaystyle q_{M}} :
磁性物质
由于外磁场的作用,磁性物质会响应出磁化强度和由这磁化强度产生的磁场。这响应通常很微弱,只有在外磁场作用时才会存在。“磁性”这术语专门形容这些物质如何响应,并且用来分类物质的磁相。按照各种物质的磁,可以分为几类:
抗磁性物质响应出的磁化强度与外磁场呈相反方向,会趋于朝着磁场较弱的区域移动,即被磁场排斥 。
顺磁性物质响应出的磁化强度与外磁场呈相同方向,会趋于朝着磁场较强的区域移动,即被磁场吸引 。
铁磁性物质内部有很多未配对电子。由于交换作用( exchange interaction ),这些电子的自旋趋于与相邻未配对电子的自旋呈相同方向。由于铁磁性物质内部又分为很多磁畴,虽然磁畴内部所有电子的自旋会单向排列,造成“饱和磁矩”,磁畴与磁畴之间,磁矩的方向与大小都不相同。所以,未被磁化的铁磁性物质,其净磁矩与磁化矢量都等于零。假设施加外磁场,这些磁畴的磁矩还趋于与外磁场呈相同方向,从而形成有可能相当强烈的磁化矢量与其感应磁场。随着外磁场的增高,磁化强度也会增高,直到“饱和点”,净磁矩等于饱合磁矩。这时,再增高外磁场也不会改变磁化强度。假设现在撤除外磁场,则铁磁性物质仍能保存一些磁化的状态,净磁矩与磁化矢量不等于零。所以,经过磁化处理后的铁磁性物质具有“自发磁矩”。
反铁磁性物质内部的相邻价电子的自旋趋于相反方向。这种物质的净磁矩与磁化强度都等于零。大多数反铁磁性物质只存在于低温状况。假设温度超过奈尔温度,则通常会变为顺磁性物质。
亚铁磁性物质内部是由两种以上原子组成,不同次晶格的不同原子,其磁矩的方向相反,数值大小不相等,所以,净磁矩与磁化强度都不等于零,具有较微弱的铁磁性。
超导体(和铁磁超导体) :当温度低于某临界温度,磁场小于某临界磁场时,这些物质会特征地变成完美导电体,电导率变得无穷大,磁性也变得非常显著,当磁场小于某更小的临界磁场时,这物质会成为完美抗磁性物质。超导体常常会在某宽广的温度和磁场值域内(称为“混合态”),展现出磁化强度对于磁场的复杂磁滞依赖关系。
对于顺磁性物质或抗磁性物质,磁化强度 M {\displaystyle \mathbf {M} } 与H场 H {\displaystyle \mathbf {H} } 之间的关系通常是线性关系:
其中, χ χ --> m {\displaystyle \chi _{m}} 是磁化率。
因此,B场 B {\displaystyle \mathbf {B} } 与H场 H {\displaystyle \mathbf {H} } 之间的关系为
其中, μ μ --> ′ = μ μ --> 0 ( 1 + χ χ --> m ) {\displaystyle \mu "=\mu _{0}(1+\chi _{m})} 是磁导率。
对于某些物质,磁导率可能是一个二阶张量,B场与H场可能呈不同方向。这些B场与H场之间的关系是本构方程( constitutive equation )的例子。超导体和铁磁性物质的B场与H场之间的关系更加复杂。详尽细节,请参阅磁滞现象。
电磁学:电场与磁场之间的关系
法拉第电磁感应定律:含时磁场生成的电场
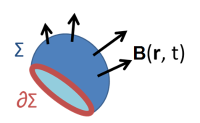
在时间 t {\displaystyle t} ,以闭回路 C {\displaystyle \mathbb {C} } 为边缘的曲面 S {\displaystyle \mathbb {S} } ,和在此曲面 S {\displaystyle \mathbb {S} } 某些位置的磁场 B ( r , t ) {\displaystyle \mathbf {B} (\mathbf {r} ,\,t)} 。
在时间 t {\displaystyle t} 通过任意曲面 S {\displaystyle \mathbb {S} } 的磁通量 Φ Φ --> B ( t ) {\displaystyle \Phi _{B}(t)} 定义为
其中, Φ Φ --> B {\displaystyle \Phi _{B}} 是磁通量, r {\displaystyle \mathbf {r} } 是场位置, d a {\displaystyle \mathrm {d} \mathbf {a} } 是微小面元素。
法拉第电磁感应定律阐明,通过任意曲面的磁通量变化率的负值,等于这任意曲面的边缘所形成的封闭回路的电动势:
假设曲面 S {\displaystyle \mathbb {S} } 固定不动,则磁通量对于时间的全导数可以改为偏导数,可以移进积分符号:
根据法拉第电磁感应定律,含时磁场会生成电动势。假设,一块磁铁移动通过导环圈,由于磁场是含时磁场,会生成电动势,驱使感应电流于导环圈。这是许多电动机和发电机的运作原理,注意到法拉第电磁感应方程内的负号是必需的,它意味着感应电流所生成磁场会反抗这含时磁场的改变。这现象称为楞次定律。
与静电学里电场的物理行为迥然不同,电场沿着闭回路的电场环流量不等于零,而会等于电动势 :
其中, E {\displaystyle \mathbf {E} } 是电场, C {\displaystyle \mathbb {C} } 是曲面 S {\displaystyle \mathbb {S} } 边缘的闭回路。
所以,沿着闭回路 C {\displaystyle \mathbb {C} } 的电场与通过曲面 S {\displaystyle \mathbb {S} } 的磁场之间的关系为
应用斯托克斯定理,这积分方程可以变为微分方程:
这是麦克斯韦方程组的四条方程中的一条。
麦克斯韦-安培方程:含时电场生成的磁场
1861年,麦克斯韦将安培定律方程重新推导一遍,使得符合电动力学条件,并且发表结果于论文《论物理力线》内。麦克斯韦认为,含时电场会生成磁场,假若电场含时间,则前述安培定律方程不成立,必须加以修正。经过修正后,新的方程称为 麦克斯韦-安培方程 ,是麦克斯韦方程组中的一个方程,以积分形式表示为
其中, S {\displaystyle \mathbb {S} } 是边缘为 C {\displaystyle \mathbb {C} } 的任意曲面, J {\displaystyle \mathbf {J} } 是曲面 S {\displaystyle \mathbb {S} } 的电流密度, D {\displaystyle \mathbf {D} } 是电势移。
以微分形式表示,
位移电流密度 J D {\displaystyle \mathbf {J} _{D}} 定义为
位移电流密度分为两个部分:
其中, P {\displaystyle \mathbf {P} } 是电极化强度。
这方程右手边的第一个项目是麦克斯韦修正项目,在任何地方都可存在,甚至在真空也可存在,虽然不涉及任何真实的电荷运动,但是,它描述一个含时电场的物理行为,就好像是真实的电流。第二个项目是电极化电流密度,与电介质内单独分子的极化性有关。由于增添了位移电流,电场与磁场能够以电磁波的形式传播于空间(详尽细节,请参阅电磁波条目)。
麦克斯韦方程组
从麦克斯韦方程组,麦克斯韦于1865年推导出电磁波方程,一种波动方程,这清楚地显示出电场和磁场的波动本质。因为电磁波方程预测的电磁波速度与光速的测量值相等,麦克斯韦推论光波也是电磁波。
与所有矢量场一样,磁场具有两种重要的数学性质,将磁场与其源头(对于磁场而言,即电流和含时电场)连结。这两个性质与电场的两个对应性质,在麦克斯韦方程组里,表达的淋漓尽致。麦克斯韦方程组和洛伦兹力方程可以完整地解释经典电磁学里所有的现象和效应。
第一种数学性质是矢量场的散度 ∇ ∇ --> ⋅ ⋅ --> Z {\displaystyle \nabla \cdot \mathbf {Z} } ,即矢量场 Z {\displaystyle \mathbf {Z} } 怎样从某一点流出。如同前面所述,磁场线永远不会开始或终结于某一点,其磁场线会形成一完整回路。用数学说法,就是磁场的散度等于零(这种矢量场称为零散度矢量场,或螺线矢量场)。高斯磁定律专门陈述这性质,也就是磁荷不存在,或磁单极子不存在的事实。迥然不同,电场线开始或终结于电荷,其散度不等于零,与电荷密度成正比。这性质称为高斯定律。
第二种数学性质是矢量场的旋度 ∇ ∇ --> × × --> Z {\displaystyle \nabla \times \mathbf {Z} } ,即矢量场 Z {\displaystyle \mathbf {Z} } 怎样弯卷或环绕于某一点。旋度的结果是环流源头的状况。磁场和电场的旋度方程分别为麦克斯韦-安培方程和法拉第电磁感应方程。
简短地说,麦克斯韦方程组的四个方程分别为:电荷是如何产生电场的高斯定理;论述了磁单极子的不存在的高斯磁定律;电流和含时电场是怎样产生磁场的麦克斯韦-安培定律,以及含时磁场是怎样产生电场的法拉第电磁感应定律。采用国际单位制,麦克斯韦方程组表示为
其中, ρ ρ --> {\displaystyle \rho } 是电荷密度, Q {\displaystyle Q} 是总电荷量, Φ Φ --> E {\displaystyle \Phi _{E}} 是电通量。
如同前面所述,响应外电场或外磁场,物质会自己制造出对应的束缚电荷或束缚电流,这些物理量的计算比较麻烦。为了避开这问题,可以使用H场和电势移场,这样,麦克斯韦方程组可以以自由电流密度 J f {\displaystyle \mathbf {J} _{f}} 和自由电荷密度 ρ ρ --> f {\displaystyle \rho _{f}} 来重新表述:
这方程组并不比原本方程组更具有一般性。解析整个问题,还需要补足B场与H场之间的关系式,和电场与电势移场之间的关系式。但是,当这些关系式很简单时,则可以避免计算束缚电荷和束缚电流。
电场与磁场:同样现象的不同表态
根据狭义相对论,电磁力的分隔为电场部分和磁场部分并不具有绝对性,而是依观测者的参考系而定;在某一参考系的观测者所观测到的纯电场力,在另一参考系的观测者可能会观测为电场力与磁场力的合力;又在某一参考系的观测者所观测到的纯磁场力,在另一参考系的观测者可能会观测为电场力与磁场力的合力。
更具体地说,在狭义相对论里,电场与磁场综合成为二阶张量,称为电磁张量。改变参考系会搅混这电磁张量的分量,改变每一个分量的数值。这种综合类似于狭义相对论将时间与空间综合成为时空,或将动量与能量综合成为四维动量。
磁矢势
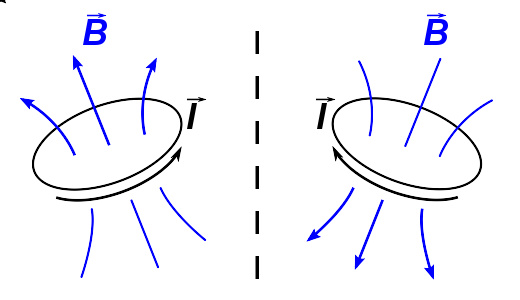
像所有的轴矢量一样,经过镜子反射,磁场会改变正负号。一条载流循环(黑色),经过镜子(虚线)反射,则载流循环所产生的磁场,不只是被镜子反射,而是被反射与逆反。
在进阶学术领域里,像量子力学或相对论,使用位势来表述电动力学,而不使用电场或磁场,是一种比较便利的方法。采用位势表述,磁矢势 A {\displaystyle \mathbf {A} } 与电势 φ φ --> {\displaystyle \varphi } 分别如此定义:
磁矢势 A {\displaystyle \mathbf {A} } 可以诠释为“广义势动量每单位电荷” ,就如同电势 φ φ --> {\displaystyle \varphi } 诠释为广义势能每单位电荷。
从数学方面来说,由于磁场是一个矢量叉积运作的结果,磁场是一种轴矢量( axial vector )。如右图所示,由于右手定则严格要求,在镜子里看到的一条载流循环,其生成的磁场在镜子里的镜像会被逆反,而普通矢量,像速度矢量,只会显示出其镜像。
麦克斯韦方程组,假若以位势表达,可以铸造成一种令人满意的形式,特别适用于狭义相对论 。 A {\displaystyle \mathbf {A} } 与 φ φ --> {\displaystyle \varphi } 共同综合成电磁四维势。使用电磁四维势比较使用电磁张量简单的多,又可以很容易地修改成合乎量子力学的形式。
量子电动力学
在现代物理学里,物理学家认为电磁场不是经典场,而是量子场;电磁场不是由在空间的每一点具有三个数值的矢量所代表,而是在每一个点具有三个量子算符的矢量。量子电动力学是一种能够准确地描述电磁作用的理论 。量子电动力学被包括于一种更完备的理论,称为粒子物理学的标准模型。
在量子电动力学里,带电粒子(或反粒子)彼此之间的电磁作用,是使用摄动理论计算获得;这相当复杂的公式可以用费曼图表现出来;在费曼图里,带电粒子借着互相交换虚光子来完成彼此之间的电磁作用。
量子电动力学应是物理史上最为准确的物理理论。量子电动力学的理论预测与实验结果的相符合能够达到非常高的准确度:现在大约为10 (限制于实验误差) 。更详尽细节,请参阅条目高准确度量子电动力学实验( precision tests of QED )
这篇文章内所有展示的方程都是取经典近似而得到的,无法用来解释量子现象与效应,但是,对于大多数日常状况,应是绰绰有余。
重要应用领域
地磁场
地磁场示意图将地球的磁场源表示为一块大磁铁,其指南极是在地球的地磁北极下面很深的位置。
地核的外核部分含有熔化的铁金属和镍金属。科学家认为,这熔液的对流运动会产生从东方朝向西方的电流,继而产生磁场,即“地磁场”。这理论称为发电机理论。由于地磁场的存在,放置于地球表面任意位置的指南针,其指北极会指向北方,指向地球的地磁北极。这性质通常可以用来定义磁铁的指北极。假设地球被视为一块大磁铁,因为异性磁极相互吸引,同性磁极相互排斥,这块大磁铁的指南极应该在地磁北极附近,其指北极应该在地磁南极附近。
右图显示出地磁场的磁场线。在地球表面大多数位置,除了南/北分量以外,磁场还具有显著的上/下分量。由于地球的磁极与地极并不恰巧重复在一起,磁场具有些微的东/西分量。
地磁场不是毫无变化的,它的强度与地磁极位置会改变。科学家发现,地磁极会周期性地逆反定向,这过程称为地磁反转。最近一次的反转是大约78万年前的布容尼斯-松山反转。对于澳大利亚红英安岩和枕状玄武岩的古地磁学研究发现,地磁场的存在,估计至少35亿年之久 。地磁场会在太空与太阳风和其它带电粒子群流互相作用,因而形成磁层。地球磁层并不是球状的,在面对太阳的一面,其边界离地心的距离约为七万千米(随太阳风强度的不同而变化)。
旋转磁场

由三卷不同相位线圈产生的磁场(以蓝色箭矢表示)所形成的旋转磁场。
理想的旋转磁场会以等角速度改变磁场方向。旋转磁场是交流电动机运作的重要机制。尼古拉·特斯拉在他的自传里写到,于1882年,他想出了旋转磁场的点子。1888年,他在这方面的研究成果获得 美国专利 381,968 。
使用两卷线圈,彼此的磁场方向互相垂直,各自通过的交流电的相位差为90°,就可以制出旋转磁场。使用三卷彼此之间的几何角度为120°的线圈,各自通过的电流,大小相同,相位差为120°,可以制出旋转磁场。三相系统能够制出适用于电动机的高品质旋转磁场,这是全世界大多数电力供应系统都使用三相系统的主要原因之一。
霍尔效应
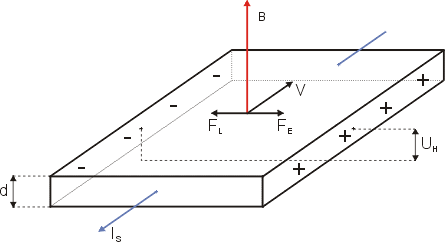
霍尔效应实验证实,金属导体的电荷载子是电子,而不是离子。
如左图所示,假设,处于磁场的一条宽片型载流导线,其电流垂直于磁场,则其电荷载子会因为感受到洛伦兹力而偏向一边,从而在垂直于磁场、电流的方向产生电压于导线两侧。1879年,艾德温·霍尔( Edwin Hall )发现这效应,称为霍尔效应。由于能够辨明电荷载子到底带有正电还是带有负电,这效应最先证实,在载流导线里流动的电流,是由移动中的电子形成的,与质子无关。
磁强计应用霍尔效应为运作原理,可以用来测量磁场,或检查像不銹钢管道一类物体因腐蚀而产生的磁通量泄漏( magnetic flux leakage )。由于霍尔效应元件产生的讯号幅值非常微弱,必须加以放大,才能被侦测,所以,现在许多霍尔效应感测器都加入一个高增益集成电路放大器。霍尔效应感测器可以用来测量磁场、旋转速度、液体流速、电流、压力等等。
在半导体领域,霍尔效应也可以应用于侦测在半导体一类物质内的主要电荷载子是负电子还是正空穴。
霍尔效应推进器是一种低功率的离子推进器。当太空船进入轨道或太空时,可以用霍尔效应推进器来推进太空船。
磁路
H场在磁路学领域很有用处。在一个线性物质内部,
其中, μ μ --> ′ {\displaystyle \mu "} 是磁导率。
这方程的形式与欧姆定律很类似:
其中, J {\displaystyle \mathbf {J} } 是电流密度, σ σ --> {\displaystyle \sigma } 是电导, E {\displaystyle \mathbf {E} } 是电场。
将这比拟加以延伸,在静磁学里相当于巨观欧姆定律 I = V / R {\displaystyle I=V/R} 的是
其中, Φ Φ --> = ∫ ∫ --> B ⋅ ⋅ --> d a {\displaystyle \Phi =\int \mathbf {B} \cdot \mathrm {d} \mathbf {a} } 是电路的磁通量, F = ∫ ∫ --> H ⋅ ⋅ --> d l {\displaystyle F=\int \mathbf {H} \cdot \mathrm {d} \mathbf {l} } 是磁动势, R m {\displaystyle R_{m}} 是磁阻。
采用这比拟,借用电路理论( cirt theory )发展出的技巧,可以很直接地计算复杂磁场几何的磁通量。
参阅
磁流体力学
发电机原理
磁场观察膜
亥姆霍兹线圈
进阶阅读
Griffiths, David J., Introduction to Electrodynamics(3rd ed.), Prentice Hall, 1998, ISBN 0-13-805326-X
Jackson, John D., Classical Electrodynamics(3rd ed.), John Wiley & Sons, 1999, ISBN 0-471-30932-X, OCLC 224523909
Tiple, Paul, Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics(5th ed.), W. H. Freeman, 2004, ISBN 0-7167-0810-8, OCLC 51095685
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

相关资料

- 有价值
- 一般般
- 没价值








推荐阅读
关于我们

APP下载