实数的绝对值

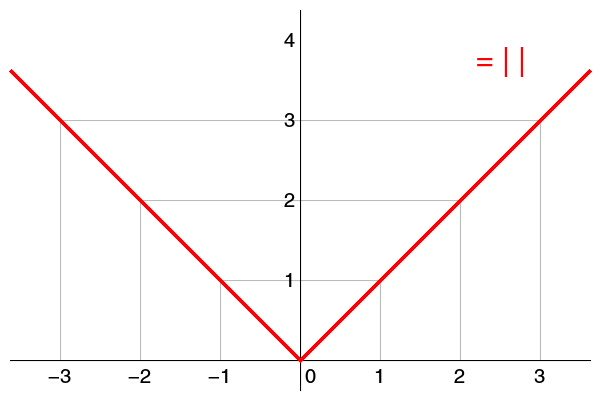
实数绝对值的平面座标图

若实数 a≠ ≠ -->0{\displaystyle a\neq 0}，则在两对称互对称的数 a{\displaystyle a} 和 − − -->a{\displaystyle -a} 中必有且仅有一个数大于 0，这个大于 0 的数就称为数 a{\displaystyle a} 和数 − − -->a{\displaystyle -a} 的绝对值，记为 |a|=|− − -->a|{\displaystyle \left|a\right|=\left|-a\right|} ，0 的绝对值为 0 。 一个数的绝对值永远非负，没有负号，某数的绝对值表示为 |{\displaystyle |} 某数 |{\displayst实数e |} 。对于所有实数x{\displaystyle x} ：若 x{\displ负数style x} 是负数， |x|=− − -->x{\displaystyle |x|=-x} （即是 − − -->x{\displaystyle -x} 是一个正数）；若 x{\displaystyle x} 非负， |x|=x{\displaystyle |x|=x} 本身。即：

一个数的绝对值可以视为该数在数线上的点和零的距离。例如 3 同时是 3 和 -3 的绝对值。

绝对值有以下性质：

|a|≥ ≥ -->0{\displaystyle |a|\geq 0}

若 a=0{\displaystyle a=0}，|a|=0{\displaystyle |a|=0}

|ab|=|a||b|{\displaystyle |ab|=|a||b|}

若 b≠ ≠ -->0{\displaystyle b\neq 0}，|ab|=|a||b|{\displaystyle |{\frac {a}{b}}|={\frac {|a|}{|b|}}}

|a+b|≤ ≤ -->|a|+|b|{\displaystyle |a+b|\leq |a|+|b|} 三角不等式不等式)

|a− − -->b|≥ ≥ -->||a|− − -->|b||{\displaystyle |a-b|\geq {\Big |}{\big |}a{\big |}-{\big |}b{\big |}{\Big |}}

若 a>0{\displaystyle a>0}，则a=|a|{\displaystyle a=\left|a\right|}；若a<0{\displaystyle a|a|{\displaystyle a=-\left|a\right|}

复数的绝对值

复数的绝对值定义为：若z=a+ib{\displaystyle z=a+ib}，则 |z|=a2+b2=zz¯ ¯ -->{\displaystyle |z|={\sqrt {a^{2}+b^{2}}}={\sqrt {z{\bar {z}}}}平方根平共轭复数轭复数）。它符合以上的六项性质，但以下的三项就未必成立：

|a|=a2{\displaystyle \left|a\right|={\sqrt {a^{2}}}}

|a|≤ ≤ -->b{\displaystyle |a|\leq b} 当且仅当 − − -->b≤ ≤ -->a≤ ≤ -->b{\displaystyle -b\leq a\leq b}

|a|≥ ≥ -->b{\displaystyle |a|\geq b} 当且仅当 a≤ ≤ -->− − -->b{\displaystyle a\leq -b}或b≤ ≤ -->a{\displaystyle b\leq a}

但此时有

|z¯ ¯ -->|=|z|{\displaystyle |{\bar {z}}|=|z|}

zz¯ ¯ -->=|z|{\displaystyle {\sqrt {z{\bar {z}}}}=|z|}

最后两道式子常用于计算涉及复数绝对值的不等式。

有序环上的绝对值

绝对值的定义可以照搬到有序环上。定义如下：

其中 − − -->a{\displaystyle -a} 是 a{\displaystyle a} 的加法反元素，而 0 是有序环的加法单位元素。

域上的绝对值

在抽象的域上，我们用绝对值的基本性质来推广定义。一个域 F{\displaystyle F} 上的绝对值是一个函数 |⋅ ⋅ -->|:F→ → -->R{\displaystyle |\cdot |:F\rightarrow \mathbb {R} }，满足以下四条公理:

由以上公理可以导出 |1|=1{\displaystyle |1|=1}。距离函数 d(x,y)=|x− − -->y|{\displaystyle d(x,y)=|x-y|} 赋予 F{\displaystyle F}度量空间结构。

如果将定义中的三角不等式换作以下较强的形式（有时又叫做强三角不等式）

则称 (F,|⋅ ⋅ -->|){\displaystyle (F,|\cdot |)}为超度量域，或称绝对值 |⋅ ⋅ -->|{\displaystyle |\cdot 阿基米德满足阿基米德性质；反之则称 |⋅ ⋅ -->|{\displaystyle |\cdot |} 满足阿基米德性质。。

超度量域的典型例子是p进数域。一般来说，值群在 R{\displaystyle \mathbb {R} } 里的赋值环对应到超度量域，此时赋值与绝对值的关系由 |x|:=av(x){\displaystyle |x|:=a^{v(x)}} 给出，其中 a∈ ∈ -->]0,1[{\displaystyle a\in ]0,1[}；不同的 a{\displaystyle a} 给出等价的拓扑结构。

微积分

绝对值函数在 x=0 不可导。

其中 C 是积分常数。

算法

C 语言关于绝对值的函数有： abs(), labs(), llabs()（在 C99 中），fabs()、fabsf() 与 fabsl() 函数计算一个对象的绝对值。当输入值不是最大负整数时，很容易写出计算绝对值的宏或函数。

以下宏可接受整数或浮点数：

#define abs(i) ((i)>0 ? (i) : (-i))

如果以函数计算，需要写多个函数，多载来处理不同数据类型：

intabs(int);floatabs(float);doubleabs(double);intabs(inti){if(i>0){returni;}else{return-i;}}

关于浮点数的绝对值算法就要用点技巧，因为要为无穷大及NaN（Not a Number）撰写特别的程式码。

在 Pascal、Fortran和Matlab语言里，取得绝对值的函数是 abs，可以计算整数、实数，以及复数。

如以组合语言撰写，应有可能以三行指令在暂存器内完成绝对值的判断与转换算法，以下例子是 x86 结构上的 32 位元暂存器，采英特尔语法。

cdqxoreax,edxsubeax,edx

cdq 指令将带号位元（sign bit）的 eax 转成 edx。如果 eax 是非负值，那 edx 变成 0，接下来的两个指令会没有影响，eax 将不变。如果 eax 是负数，那么 edx 会变成 0xFFFFFFFF ，或是 -1。接下来的两个指令会变成倒转的二补数，并从 eax暂存器中取得负数的绝对值。

参考资料

Nahin, Paul J.;An Imaginary Tale; Princeton University Press; (hardcover, 1998). ISBN 0-691-02795-1

O"Connor, J.J. and Robertson, E.F.;"Jean Robert Argand"

Schechter, Eric; Handbook of Analysis and Its Foundations, pp 259-263,"Absolute Values", Academic Press (1997) ISBN 0-12-622760-8

MathWorld上Absolute Value的资料，作者：埃里克·韦斯坦因。

absolute value atPlanetMath.

微积分学教程，( 第一卷 ) ( 第 8 版 )，第 3 页，ISBN 5-9221-0436-5，菲赫金哥尔茨 著，杨弢亮 、叶彦谦 译，郭思旭 较，高等教育出版社

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。