历史

第一个系统地推算概率的人是16世纪的卡尔达诺 。记载在他的著作Liber de Ludo Aleae中。书中关于概率的内容是由Gould从拉丁文翻译出来的。

Cardano的数学著作中有很多给赌徒的建议。这些建议都写成短文。例如：《谁，在什么时候，应该赌博？》、《为什么亚里士多德谴责赌博？》、《那些教别人赌博的人是否也擅长赌博呢？》等。

然而，首次提出系统研究概率的是在帕斯卡和费马来往的一系列信件中。这些通信最初是由帕斯卡提出的，他想找费马请教几个关于由Chevalier de Méré提出的问题。Chevalier de Méré是一知名作家，路易十四宫廷的显要，也是一名狂热的赌徒。问题主要是两个：掷骰问题和比赛奖金应分配问题。

概念

在日常生活中，我们常常会遇到一些涉及可能性或发生机会等概念的事件（event）。一个事件的可能性或一个事件的发生机会是与数学有关的。例如：

“从一班40名学生中随意选出一人，这人是男生吗？”

事实上，人们问“……可能会发生吗？”时，他们是在关注这个事件发生的机会。在数学上，事件发生的机会可用一个数来表示。我们称该数为 概率 （Probability）。

我们日常所见所闻的事件大致可分为两种：

一种是确定件。确定件包含必然事件和不可能事件。 如太阳从东方升起，或者在标准大气压下，水在100℃时会沸腾。我们称这些事件为必然事件。 如掷一个普通的骰子，向上一面的数字是7。我们称这些事件为不可能事件。

此外，有大量事件在一定条件下是否发生，是无法确定的。如明天的气温比今天低、掷一枚硬币得正面向上，又或者在下一年度的NBA比赛中，芝加哥公牛队会夺得全年总冠军。像以上可能发生也可能不会发生的事件称为随机事件。

理论

概率论是一种用正式的用语表达概率概念的方式，这些词语可以用数学及逻辑的规则处理，结果再转换到和原来问题有关的领域。

至少有两种成功的将概率公式化的理论，分别是柯尔莫哥洛夫公式化以及 考克斯 （ 英语 ： Cox ） 公式化。在柯尔莫哥洛夫公式化（参考概率空间）中，用集合代表事件，概率则是对集合的测度。在 考克斯定理 （ 英语 ： Cox"s theorem ） 中，概率是不能再进一步分析的基元，强调在概率值及命题之间建立一致性的关系。在二种公式化方法中，概率公理都相同，只有一些技术细节不同。

有其他量度不确定性的方式，例如 Dempster-Shafer理论 （ 英语 ： Dempster–Shafer theory ） 或是 可能性理论 （ 英语 ： possibility theory ） ，但两者都有本质上的不同，无法和一般了解的概率论相容。

应用

概率的概念常常应用在生活中，例如风险评估及以金融市场的交易等。政府也在环境法中应用概率，称为路径分析（pathway analysis）。例如中东冲突可能会对油价有某程度的影响，而油价对世界经济可能会有涟漪效应的影响。某个油品交易商认为中东冲突会使油价上升或下降，并将他的意见提供给其他交易商。因此概率不是各自独立的进行评估，评估的过程也不一定合理。行为经济学就是描述团体迷思对定价、政策甚至和平或冲突的影响 。

有关概率评估及组合的严谨方式也改变了社会。对大部分的社会大众而言，重要的是了解概率评估的方式以及概率和决策之间的关系。

概率理论另一个明显的应用是 可靠度理论 （ 英语 ： Reliability theory ） 。像汽车及消费性产品会在产品开发时应用可靠度理论来减少产品失效的概率。失效概率会影响厂商在产品保用证上的决策 。

像自然语言处理中用的 快取语言模型 （ 英语 ： cache language model ） 及其他语言模型等也属于是概率理论的应用。

数学处理

事件 A 的概率一般会写成 P ( A )、 p ( A )或Pr( A ) 。概率的数学概念可延伸到无限的样本空间甚至不可数的样本空间，但需要用上概率测度的概念。

概率的公理化定义将概率的相关范畴从具体问题中抽象出来，从而可以在数学意义下考察概率的相关概念和由之引出的问题。以下给出概率的公理化定义：

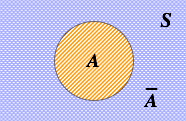
设随机事件的样本空间为Ω，Ω的一个子集称为事件。对于Ω中的每一个事件A，都有实函数P(A)，满足：

非负性： P ( A ) ≥ ≥ --> 0 {\displaystyle P(A)\geq 0} ；

规范性： P ( Ω Ω --> ) = 1 {\displaystyle P(\Omega )=1}

可数可加性：对可数个两两互斥事件{A i } i∈ N 有： ∑ ∑ --> i = 1 ∞ ∞ --> P ( A i ) = P ( ⋃ ⋃ --> i = 1 ∞ ∞ --> A i ) {\displaystyle {\displaystyle \sum _{i=1}^{\infty }P(A_{i})=P\left(\bigcup _{i=1}^{\infty }A_{i}\right)}}

任意一个满足上述条件的函数P都可以作为样本空间Ω的概率函数，称函数值P(A)为Ω中事件A的概率。

表示概率

一个事件的概率值通常以一个介于0到1的实数表示。一个不可能事件其概率值为0，而确定事件其概率值则为1。 但反推并不一定成立，也就是说概率值为0的事件不表示它就是一个不可能事件，同理，概率值为1的事件不表示它就一定发生。例如，在一个正方形内作一条线段，由于这条线段的面积是0，所以一个点落在这条线段上的概率就是0，但它并不是不可能事件。

实际上大多数的概率值都是介于0与1之间的数，这个数示代表事件在"不可能发生"与"确定发生"之间的相对位置。事件的概率值越接近1，事件发生的机会就越高。

举例来说，假设两个事件有相同的发生概率，就像被抛掷而落地的铜板不是正面向上就是反面向上一样，但是我们不能说：每2次抛掷会出现1次，只能说事件发生的概率是平均每2次出现一次，或说是 "50%" 或 "1/2"。

分布

概率分布函数是一个把概率分配给事件或者命题的函数。对于任何一个事件或者命题，总有很多分配概率的方法，所以选择不同的分布等同于对一个问题中的事件或者命题作出不同的假设。

分布还可分为“离散”和“连续”的。

概率计算总结

和随机的关系

在牛顿力学的概念中，决定论的世界中，若所有条件都是已知，都没有任何概率性的成分在内（拉普拉斯的恶魔），不过有可能一些系统对初始条件敏感，敏感程度甚至到超过可能量测的范围。以俄罗斯轮盘为例，若手的施力，出力的时间等资讯已知，轮盘最后停止的位置是可以计算而得的，不过此时需要知道轮盘的惯量及摩擦系数，球的质量、光滑度及圆度，出力过程中手速度的变化等。此时，相较于用牛顿力学的方式分析，概率性的描述可能更适合描述重复玩数次俄罗斯轮盘的结果。科学家发现在气体动力论中也有类似的情形，系统理论上是确定的，但因为气体分子个数约和阿伏伽德罗常数6.02·10 量级相当，因此也只能用概率性的描述。

在描述量子理论时一定会用到概率论 。二十世纪初期，物理学界有一个革命性发现，所有次原子层级的物理过程有随机性，依循量子力学。物理的波函数是确定的，是数个状态的叠加，但根据哥本哈根诠释，观察会带来波函数塌缩，因此只能观察到其中一个状态。不过这种缺乏决定论的观点未受到所有人的同意。爱因斯坦在给马克斯·玻恩的信上提到“我相信上帝不会玩骰子。” 。而发现波函数的埃尔温·薛定谔认为量子力学只是内部决定论状态的统计近似 。在近代的诠释中，量子退相干有相当的概率性质。

参考文献

来源

Olofsson, Peter (2005). Probability, Statistics, and Stochastic Processes , Wiley-Interscience. p. 504. ISBN 978-0-471-67969-1

引用

^ “几”字表示数量意义，即“若干、多少”。但因为“几”字的义项较多，有人误以为“几率”的含义是指“机会”（英语为opportunity）的多少，进而误写成“機率”，数学界就另外取一个名“概率”。

参见

概率论

贝叶斯概率

伯努利过程

考克斯定理 （ 英语 ： Cox"s theorem ）

决策理论

机会游戏

信息论

平均法则

大数法则

测度论

常态分布

随机场

随机变量

统计学

随机过程

排队理论

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。