概述

在电动力学里，若考虑一带电粒子在电磁场中的受力，可以用以下的劳仑兹力定律表示：

其中， F {\displaystyle \mathbf {F} } 是劳仑兹力， q {\displaystyle q} 是带电粒子的电荷量， E {\displaystyle \mathbf {E} } 是电场， v {\displaystyle \mathbf {v} } 是带电粒子的速度， B {\displaystyle \mathbf {B} } 是磁场。

劳仑兹力定律是一个基本公理，不是从别的理论推导出来的定律。

这方程式右边有两项，第一项是电场力 F E = q E {\displaystyle \mathbf {F} _{E}=q\mathbf {E} } ，第二项是磁场力 F B = q v × × --> B {\displaystyle \mathbf {F} _{B}=q\mathbf {v} \times \mathbf {B} } 。

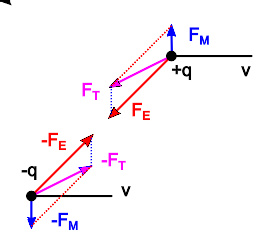
当两个带电粒子都以相同速度 v {\displaystyle \mathbf {v} } 移动时，带正电粒子 + q {\displaystyle +q} 会感受到电场力 F E {\displaystyle \mathbf {F} _{E}} 、磁场力 F M {\displaystyle \mathbf {F} _{M}} 与净力 F T {\displaystyle \mathbf {F} _{T}} ，带负电粒子 − − --> q {\displaystyle -q} 会感受到电场力 − − --> F E {\displaystyle -\mathbf {F} _{E}} 、磁场力 − − --> F M {\displaystyle -\mathbf {F} _{M}} 与净力 − − --> F T {\displaystyle -\mathbf {F} _{T}} 。注意到作用力 F T {\displaystyle \mathbf {F} _{T}} 和反作用力 − − --> F T {\displaystyle -\mathbf {F} _{T}} 不同线。在本图内，速度 v {\displaystyle \mathbf {v} } 的大小不按比例绘制。

在静电学里，场源电荷所产生的电场与试探距离的平方成反比，所以电场力与试探距离的平方成反比。在静磁学里，无法获得类似结果，因为只有移动中的电荷才会产生磁场，而移动中的点电荷无法构成平稳电流，无法用必欧-沙伐定律正确地计算出磁场。在电动力学里，应用推迟势概念，可以推导出必欧-沙伐点电荷定律。这定律给出，移动中的场源电荷所产生的电场、磁场与试探距离的平方成反比。所以，电磁力遵守平方反比定律。

作用与反作用定律又分为两种版本：强版本和弱版本。这里，第三定律所表述的是“弱版作用与反作用定律”。而“强版作用与反作用定律”，除了弱版作用与反作用定律所要求的以外，还要求作用力和反作用力都作用在同一条直线上。万有引力与静电力都遵守强版作用与反作用定律。可是，在某些状况下，作用力和反作用力并不同线（两作用点的连线）。

设想两个呈平移运动的电荷，其平移速度相同，但并不垂直于两电荷的连线。由于必欧-沙伐点电荷定律与洛伦兹力定律计算出的作用力和反作用力并不同线，这一对电磁力只遵守弱版牛顿第三运动定律。若两移动的电荷，其移动的速度互相垂直，则它们各自感受到的电磁力不遵守弱版牛顿第三运动定律。

基本交互作用

电磁力是四种基本交互作用中的一种，其他的基本交互作用有：

弱交互作用，影响所有费米子，即所有自旋为半奇数的粒子，而弱交互作用会影响所有费米子，次原子粒子的放射性衰变就是由它引起（在粒子物理学中，弱交互作用和电磁力可以用电弱相互作用来描述）。

强交互作用，束缚夸克形成核子，束缚核子形成原子核。

重力

所有其他的力（例如摩擦力）都是由这些粒子运动带来的基本交互作用及动量而来。

许多电磁力的现象都是在十九世纪发现 。而日常生活中可以感受到，超过原子尺度以外的现象，除了重力以外，其他都是因为电磁力而造成 。大致上，所有原子之间的交互作用力都可以由带电的原子核和电子之间的电磁力，以及这些粒子的动量来说明。这包括日常经验到推或拉一物体的力，可以解释为身体的分子和物体分子的分子间作用力，所有的化学现象也都是由电磁力而来。

对于原子内作用力和分子间作用力，需要了解的是因电子移动产生动量对应的等效力，以及在相互作用的原子间移动的电子，以及其带有的动量。当电子越来越密集，因着泡利不相容原理，其最小动量必须变大。物质在分子尺度下的特性（包括其密度）是靠电磁力以及电子上动量交换产生等效力的平衡所决定。

近年来研究发现，在某些状况下，电磁力和弱核作用力会统一，称为电弱交互作用，这个发现使得人类距离大统一理论更进一步，科学家阿卜杜勒·萨拉姆、谢尔登·格拉肖以及史蒂文·温伯格也因此获颁1979年的诺贝尔物理奖 。

相对论下的电磁力

在狭义相对论中的电磁交互作用会用一个称为电磁场张量的二维张量描述：

以张量方式表示，符合马克士威方程组的电磁场张量（以CGS制表示）如下：

方程式还可以用外微分及霍奇对偶写成更简洁的形式：

若方程式为以上的形式，而电磁往外延伸的区域是单连通的，则电磁场可以表示为一个电磁四维势的外导数，电磁四维势是四维势向量，和经典电磁学的势有以下的关系：

其中

上述的替换大幅增昇了方程式的分辨率，其实上，四维势向量和电磁张量的关系为：

电磁作用可以完全用定义电磁场矢量来表示，这也是现在的电磁作用会用向量表示的原因（在量子处理中，则是向量玻色子）。

在广义相对论中，在弯曲时空的电磁场和闵可夫斯基时空相近，不过偏微分会用共变导数表示。

量子电动力学

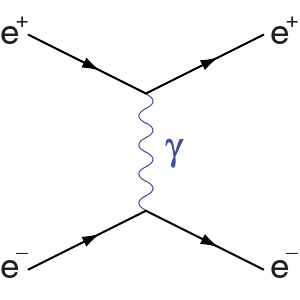
在巴巴散射里，电子与正电子彼此之间倚赖交换光子来实现电磁力。

当进入到原子的尺度时（0.1nm），会发现所有的物质都是由不同的原子构成的，而原子是由不同的原子核与电子构成的，带负电的电子与带正电的原子核（由质子与中子构成）经由电磁作用紧密地结合在一起。

但在原子的尺度时，必须用量子化的电磁场来描述。这种描述把两粒子之间的作用看成是在交换光子。在1950年代，这种描述就已发展得相当完善了，称作量子电动力学。

量子电动力学是量子力学和电磁学的整合，在电动量子力学中，粒子和场的交互作用和光子有关，光子没有质量，属于规范玻色子，光子和带电粒子之间的交互作用造成了所有电磁学的现象。

根据能量-时间不确定性原理，

其中， Δ Δ --> E {\displaystyle \Delta E} 、 Δ Δ --> t {\displaystyle \Delta t} 分别是能量、时间的不确定性， ℏ ℏ --> {\displaystyle \hbar } 是约化普朗克常数。

一个质量为 m {\displaystyle m} 的媒介粒子最多只能存在 T ≈ ≈ --> ℏ ℏ --> / m c 2 {\displaystyle T\approx \hbar /mc^{2}} 时间，否则，能量-时间不确定性原理会被违反。在时间 T {\displaystyle T} 内，这媒介粒子只能移动 c T {\displaystyle cT} 距离，因此，作用力的作用范围 R {\displaystyle R} 大约为

例如，W玻色子的质量为80GeV，所以，弱力的作用范围大约为10 m。

由于光子的质量为零，电磁力的作用范围为无穷远。

计量和单位

参见

电磁学

电学

磁学

重力

强核作用力

弱核作用力

量子色动力学

电弱统一理论

大统一理论

参考资料

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。