理论史

牛顿的万有引力定律

在1687年，艾萨克·牛顿在他的《自然哲学的数学原理》一书中发表了万有引力定律。牛顿的万有引力定律的陈述如下：

如果两个质点的质量分别为 m 1 {\displaystyle m_{1}} 、 m 2 {\displaystyle m_{2}} ，并且在它们之间的距离为 r {\displaystyle r} ，则它们之间的万有引力 F {\displaystyle F} 为

其中， G {\displaystyle G} 是被称为引力常数（或万有引力常数），2014年CODATA推荐的引力常数值是 G = ( 6.67408 ± ± --> 0.00031 ) × × --> 10 − − --> 11 m 3 / ( k g ⋅ ⋅ --> s 2 ) {\displaystyle G=(6.67408\pm 0.00031)\times 10^{-11}m^{3}/(kg\cdot s^{2})} 。 注：只有当两个物体之间的距离远大于物体的几何尺寸时，物体可以近似看作质点，这个公式才是适用的。否则应当把物体分割为足够小的质点，两积分间计算引力，而后进行积分。

引力的单位有牛顿（N）或是达因（cgs），在国际单位制中，1公斤的物体在地球表面的重量大约是 9.8 k g ⋅ ⋅ --> m ⋅ ⋅ --> s − − --> 2 {\displaystyle 9.8kg\cdot m\cdot s^{-2}} 。在CGS制中，1克的物体在地球表面的重量大约是重 980 g ⋅ ⋅ --> c m ⋅ ⋅ --> s − − --> 2 {\displaystyle 980g\cdot cm\cdot s^{-2}}

广义相对论

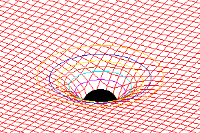
引力源附近扭曲的时空

1916年，阿尔伯特·爱因斯坦发表广义相对论，用几何语言描述的引力理论，它代表了现代物理学中引力理论研究的最高水平。广义相对论将经典的牛顿万有引力定律包含在狭义相对论的框架中。在广义相对论中，引力被描述为时空的一种几何属性（曲率）；而这种时空曲率与处于时空中的物质与辐射的能量-动量张量直接相联系，其联系方式即是爱因斯坦场方程（一个二阶非线性偏微分方程组）。

引力传播的速度

对于引力传播的速度基本有三种理论：

牛顿的超距作用观点，认为引力的传递不需要时间（速度无限大）。这理论已被相对论推翻。

引力的速度是超光速的某值。这理论也已被相对论推翻。

现在所普遍认定的是爱因斯坦所提出的说法，即引力的传播速度是真空中的光速。

相关内容

地球引力

各个行星天体，包括地球，都具有其自身的万有引力特性。假设一个球形对称的物体，对一特定位置的引力强度和物体质量成正比，和位置和物体球心的距离成反比。

一位置的引力场强度等于一物体放置在该位置时，受影响而产生的加速度。地球表面的自由落体加速度被表示为 g ，可以用以下的标准引力表示：根据国际度量衡局（BIPM）的资料，标准引力为9.80665m/s 或者32.1740ft/s 。

这表明，如果忽视空气阻力的影响，在地表附近正在自由落体的物体速度每秒将增加9.81 m/s（大约22mph）。因此，一个从静止开始下落的物体在一秒后的速度将达到9.81 m/s，第二秒将达到19.62 m/s，以后的情况也将依此类推。

若一质量和地球相当的物体（图中较小的圆）接近地球（图中较大的圆），则可以观测到地球因受吸引而产生的加速度

根据牛顿第三运动定律，地球同时也受到下落的物体等值反向的力的作用，意味着地球也将加速向物体运动。但是，由于地球巨大的质量，这个加速度小到难以察觉。

自由落体方程组

在一般情况下，物体因不变的引力持续作用而运动时，一组动力学方程组可描述它运动的轨道。例如，牛顿万有引力定律给出了一个简单的方程 F = mg ，其中 m 代表物体的质量。当物体自由落体向地球的距离可以以我们日常用到的距离衡量时，这个猜想是合理的；但若用于对大距离譬如太空船的轨道进行计算时，这将导致极大的误差。

万有引力和天文学

牛顿的万有引力定律的发现和应用被用于计算和了解我们的太阳系内各个行星的详细信息、太阳的质量、恒星间的距离，甚至被用于推测暗物质理论。尽管人类还没有去过太阳和其他星球，我们都可以知道它们的质量。这些都是通过万有引力定律研究得出的。在空间中任何物体都按照一定的轨道围绕某些大质量物体运转，它们之间的万有引力保持着它们的轨道。行星围绕恒星运转，恒星围绕星系中心运转，星系围绕星团中心运转，星团围绕超星系团运转。

万有理论

在上个世纪，另外三大基本相互作用：强相互作用、弱相互作用和电磁相互作用的产生机制已经通过传递相对作用的规范玻色子的观念加以解决。现在人们正在尝试将规范玻色子、相对论与万有引力联合成为一个统一的整体。因此，引力相互作用是如何与其他三个基本作用互相影响的是一个未决问题。

应用

极大数量的机械发明的正常运行在某种程度上依赖于引力而实现。例如，高度差可以提供有用的液压，这是静脉滴注和水塔的运作原理。利用水的引力势能发电的水力发电装置亦可以这种能量将电车推上斜坡。同样，缆绳上悬挂的重物可通过滑轮使缆绳及缆绳位于滑轮另一边的那一部分持续地绷紧。

还有更多的例子：比如说熔铅，当铅水从霰弹塔的顶端灌入后，会变成一颗颗如雨点一般散落的铅弹——首先被分离成为多个小液滴，形成熔融状态的球体，之后逐渐凝固为固体，并在被众多相同的熔融石的共同作用下，最终在自由落体中冷却形成球形或近球形。引力驱动时钟由引力势能提供运行的能量，摆钟则依赖于引力来校准时间。人造卫星的正常运行则是运用牛顿《原理》计算的结果。

可供参考的理论

历史上的各种理论

亚里士多德引力理论 认为，物体的运动速度和其所受外界的合力是成正比（或者是该物体所受的自己本身的引力），并且和物体运动介质的粘度成反比。

尼可拉·特斯拉（Nikola Tesla）宣布但是从未发表的引力动力学理论；部分原因是因为理论的细节（如果有的话）并没有透露，并没有得到物理学家们的重视。

感应引力（ Induced Gravity ），由安德烈·萨哈罗夫（Andrei Sakharov）提出，认为广义相对论可能起源于量子场论。

雷萨吉万有引力理论（ Le Sage"s Theory of Gravitation ，也叫做 雷萨吉引力理论 ），由乔治-路易斯·雷萨吉（Georges-Louis Le Sage）提出，以一种充满整个宇宙轻的气体的流动来解释这种现象。

Nordström万有引力理论（ Nordström"s Theory of Gravitation ），广义相对论的早期竞争者。

怀特黑德万有引力理论，（ Whitehead"s Theory of Gravitation ）广义相对论的另一个早期竞争者。

最近的各种理论

布兰斯-迪克（Brans-Dicke）有关引力的理论（ Brans-Dicke theory ）。

纳森·罗森有关引力的理论（ Rosen Bi-metric Theory ）。

莫德采·米尔格若姆（Mordehai Milgrom）在修正牛顿引力理论（ Modified Newtonian Dynamics , MOND）中，提出在微小加速运动上对牛顿第二定律的修正。

新近提出的且被高度争论的程序物理学（ Process Physics ）理论试图处理引力问题。

自建宇宙理论（ Self Creation Cosmology ）将布兰斯-迪克理论修正为允许创造质量。

相关条目

反重力

参考资料

Halliday, David; Robert Resnick; Kenneth S. Krane. Physics v. 1. New York: John Wiley & Sons. 2001. ISBN 978-0-471-32057-9.

Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers 6th ed. Brooks/Cole. 2004. ISBN 978-0-534-40842-8. 引文格式1维护：冗余文本 (link)

Tipler, Paul. Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics 5th ed. W. H. Freeman. 2004. ISBN 978-0-7167-0809-4. 引文格式1维护：冗余文本 (link)

Jefimenko, Oleg D.，" Causality, electromagnetic induction, and gravitation : a different approach to the theory of electromagnetic and gravitational fields ". Star City [West Virginia]：Electret Scientific Co., c1992. ISBN 978-0-917406-09-6

Heaviside, Oliver，" A gravitational and electromagnetic analogy "（英文）. The Electrician, 1893.

Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia : Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton"s Principia , by I.Bernard Cohen. University of California Press 1999年ISBN 978-0-520-08816-0 ISBN 978-0-520-08817-7

Max Born（1924年）, Einstein"s Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。