名称

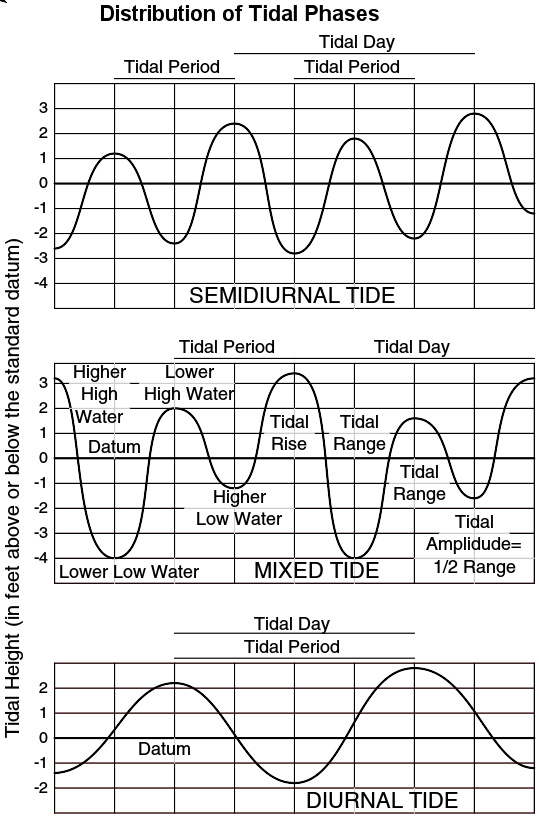
潮汐的时间分布。

地球上的海水或江水，受到太阳、月球的引力以及地球自转的影响，在每天早晚会各有一次水位的涨落，这种现象，早称之为潮，晚称之为汐。

海面上升达最高时，称为满潮(High water)﹔

海面下降至最低时，称为干潮(Low water)。

由干潮至满潮的期间，称为涨潮(Flood)﹔

而由满潮至干潮的期间，则称为落潮(Ebb)。

自某一次满潮至下一次满潮，或由某一次干潮至下一次干潮的时间， 称为潮汐的周期(Period of tide)。

满潮与干潮之海面高度差称为潮差(Tidal range)。

特征

潮汐是海平面以下面几个阶段变化的重复周期：

海水经历几个小时的上涨或在海滩上进展，

水达到被称为高潮的最大高度。

经历几个小时的海平面降低，或是像瀑布一样从海滩退出，

水面在所谓的低潮停止降低。

潮汐停止的瞬间称为滞水或憩潮，然后潮水会改变方向，称为转向。憩潮通常发生在潮水最高和最低的附近，但是在高低水位的时刻，它们的位置有着显著的不同 。

潮汐可能是半日潮（一天有两次高潮和两次低潮），或一日潮（每天只有一次循环）。在大多数的地区，潮汐都是半日潮。每天的分担是不同的，因此在选定的日子里，两次高潮的高度不同（日均差）。在潮汐表内，会有不同的高高潮和低高潮。同样的，每天的两次低潮也会有高低潮和低低潮。日均差会随着时间变化，通常在月球越过赤道的时候最小 。

潮汐的组成

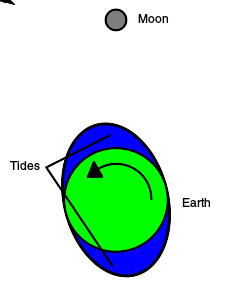
月球公转与地球自转方向相同，但地球自转速度快于月球公转，使涨潮被地球自转带着跑，在月球至中天前到来，相差约3度 。 月球与潮汐隆起（tidal bulge，或称隆堆）相互吸引，使得地球自转渐渐变慢，而月球公转渐快。这使得当前每一年月球轨道约推离地球38毫米，而地球的一日延长约23微秒。 因为月球对地球万有引力的作用，地球视作一固态整体，较背对月球一侧的海水更被拉近月球，因此背对月球一侧的海水形同“升高”了。 这造成两端的潮汐隆起与每天两次的涨潮。

潮汐的变化是多种不同周期活动最终的结果，这种影响称为潮汐的组成。

潮汐变化的时间尺度范围从数小时到一年，所以要在固定的观测站以潮汐表精确的纪录水位的高低变化，可以筛选出变化周期短于一分钟的水位变化。这些资料将会和参考值（或已知数），通常是平均海平面，做比较 。

主太阴半日潮

在大多数的地区，潮汐最主要的成分是主太阴半日潮，也称为 M 2 ，它的周期是12小时25.2分钟，正好是太阴潮汐日的一半，也是月球至下一次中天所需的一半时间，也是地球上同一个地点因为自转再一次正对着月球的周期。使用简单的潮汐钟就可以追踪这个成分的潮汐。因为月球以和地球公转相同的方向环绕着地球运转，因此太阴日比地球日长一点。以手表上的分针做比较就可以了解：分针与时针在12:00重合，但再次重合的时间是1:05，而不是1:00就可以了解了。

变动的范围：和小潮

半日潮的潮差（在半天之内水域的最高和最低位置的变化）各自有两个星期或14天周期的不同变化。在新月和满月，当太阳、月球和地球的在一条线上，也就是朔望的时刻，太阳和月亮的潮汐力迭加，潮汐的潮差会达到最大：称为（英文为 spring tide ，但与春季无关，不能译为春潮，而是在字面上源自较古老的含义：跳跃、向前喷出、上升等水文学的自然现象）。当月球在上弦或下弦的位置，从地球看到的太阳和月球相距90度， 太阳的力量抵销了部分的月球力量，使两者的合力效果最小。在月相周期的这种位置上，潮汐的潮差最小：称为小潮（英文 neap tide 的字源不清楚）。的时候，高水位高于平均值，而低水位低于平均值，憩潮的时间比平均短，但潮流比平均值强大；小潮的结果是一切都小于平均值。和小潮的时间间隔大约是7天。

月球与地球之间的距离变化也影响到潮汐的高度，当月球在近地点，潮汐的潮差会增加，而在远地点时潮汐的潮差会减少。每7.5个朔望月，新月或满月会和近点月重合，会造成近点月使潮汐的潮差达到最大。如果在此时有风暴出现在沿海地区，其结果是造成的灾害（各种形式上的财物损失，等等）会特别的严重。

半日潮潮差的差异

当一天有两次但高度不同的涨潮（也有两次高度不同的退潮），这种形式称为混合型半日潮 。

海洋测深学

滨线和海床形状的变化会改变潮汐的传播，所以潮汐时间和高度的预测不能单纯的只观测月球在天空中的位置。海岸的特性，如水下的深度和海岸的形状，都会影响到每个不同地区的潮汐预报；精确的海水高度和潮汐时间可能需要依据不同地区的海岸地形学特征对潮汐流动影响的模型来预报。但是，对给定地点的潮汐，月球的高度和满潮与干潮时间的关系（月潮间隔）是有相对应的常数和可预测的，而相同海岸的其他地点的潮汐之间也是有关联的。例如，维吉尼亚州诺福克的涨潮可预测出现在月球过中天之前的2.5小时。

大块的陆地和海滩对原本可以在全球自由流动的海水是一种障碍，它们不同的形状和大小经常会影响到潮汐的大小，结果是潮汐有不同的类型。例如，美国大陆东海岸的主要形式是单日潮，大西洋沿岸的欧洲也是如此，而美国大陆西岸的形式则是混合的半日潮 。

其它的成分

影响潮汐的因素包括太阳的引力、地轴的倾斜、月球轨道的倾角和地球与月球轨道的椭圆形状。

少于半天的周期变化称为谐振成分。反之，长周期的成分是超过一天、一个月或一年的循环。

相位和振幅

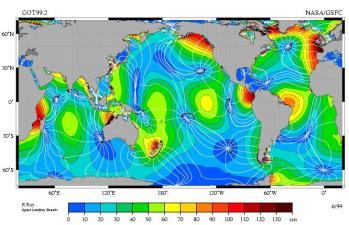
图4：M 2 潮汐的成分。振幅以颜色显示，白线为间隔一小时的等潮线。环绕无潮点的的曲线显示潮汐的方向，每个指示6小时的同步周期

因为 M 2 的成分是主宰潮汐的最主要因素，潮汐的阶段或相位，使用在满潮之后几小时来呈现是有用的概念。潮汐的阶段也可以用角度来测量，一个循环是360度。潮汐相位相同阶段的连线称为等潮线，类似地形图上的等高线。等潮线（也称为潮汐相位）沿着同时发生高潮的海岸延伸至海洋中，并且等潮线会沿着海岸推进。半日和长期相位的成分由海水每日的最高水位的高度来测量。这些与下面讨论的精确性只适用于一个单一的潮汐成分。

对一个像水盆一样被海岸线环绕的海洋，等潮线的点会快速的向内并汇聚在一个共同的点，称为无潮点。无潮点是在一次的满潮和干潮的高低水位之间，海面没有起与落，稳定不动的点（罕见的异常在潮期中经常发生在小岛和它的周围，如同环绕在新西兰和马达加斯加。）。潮汐的运动一般在扫过大陆的海岸线时会减少，因此横越过等潮线的是振幅相同的轮廓（在高潮和低潮之间一半的距离），并在无潮点衰减为零。一个半日潮的无潮点大约在潮汐钟正面的中间，时针指向满潮的等潮线的方向；它的方向与干潮的等潮线相对着。

满潮线以无潮点为中心，以等潮线上升的方向，远离退潮的等潮线，约每12小时旋转一周。由于柯氏力效应，这种转动通常在南半球是顺时针方向，而在北半球是逆时针方向。与参考潮汐相位在相位上的差异称为期。参考潮汐是在无陆地的0°经线，也就是格林威治子午线上假设的一个平衡潮成分。

在北大西洋，因为等潮线是以无潮点向逆时针方向旋转，在纽约港的满潮会比诺福克港早约一个小时。南方的哈特拉斯角的潮汐力更为复杂，因而不能只依靠北大西洋的等潮线来预测。

物理学

图5： 从北极鸟瞰的地球和月球。

潮汐物理学的历史

牛顿在他的 自然哲学的数学原理 （1687）一书中以科学的研究奠定了用数学解释潮汐发生的基础力量 。牛顿首先应用牛顿万有引力定律计算由太阳和月球吸引造成的潮汐 ，并且提供了引潮力最初的理论。但是牛顿的理论和他的后继者是采用之前拉普拉斯的均衡理论，在很大的程度上是以近似值描述潮汐即使在覆盖整个地球的非惯性海洋中也会发生 引潮力（或是相当于位能）对潮汐理论依然是有意义的，但做为一个中间的数值，而不是最终的结果；理论已经考虑地球动力学与潮汐的关系，而受到地形、地Ë球自转和其它因素的影响 。

在1740年，在巴黎的法国皇家科学院提供奖金给最佳的潮汐理论，由丹尼尔·伯努利、Antoine Cavalleri、欧拉、和柯林·马克劳林共享这笔奖金。

马克劳林使用牛顿的理论显示一个覆盖了足够深度海洋的单一平滑球体，在潮汐力的作用下会变形成为扁长的椭球体，而长轴就指向引起变形的天体。马克劳林也是第一个写下地球的柯里奥利力对运动的影响。

欧拉意识到在水平方向的力（引潮力）才是驱动潮汐的力（比垂直方向的起潮力大）。

在1744年，达朗贝尔研究潮汐的大气方程式，但没有包括转动的因素。

皮埃尔-西蒙·拉普拉斯以偏微分方程的形式制订有关海洋在水平的流动和海表面高度的系统，是第一件主要的潮汐动力理论，而且拉普拉斯潮汐方程在今天仍在使用。William Thomson, t Baron Kelvin重写了拉普拉斯方程中的涡度项目，使方程式可以描述与解决驱动沿岸陷落波，也就是所知的克耳文波 。

其他人，包括克耳文与亨利·庞加莱继续开发拉普拉斯理论，根据这些发展与E W布朗和Arthur Thomas Doodson的月球理论在1921年开发和发布 ，第一个现代化的引潮谐波形式：道森列出了388项潮汐频率 ，其中有些方法现在仍被使用着 。

力

若以月球潮汐为例，作用于每单位质量的引潮力是月球的引力场在该单位质量的位置和在地心的矢量差。此每单位质量引潮力可分解为垂直 (即径向) 分量 T v {\displaystyle T_{v}} 和水平 (即切向) 分量 T h {\displaystyle T_{h}} 。简化后，它们分别是

T v = G m R D 3 ( 3 cos 2 ⁡ ⁡ --> θ θ --> − − --> 1 ) {\displaystyle T_{v}={\frac {GmR}{D^{3}}}(3\cos ^{2}\theta -1)} 和 T h = 3 G m R 2 D 3 sin ⁡ ⁡ --> 2 θ θ --> {\displaystyle T_{h}={\frac {3GmR}{2D^{3}}}\sin 2\theta } 。

其中 G {\displaystyle G} 是万有引力常数， m {\displaystyle m} 是月球质量， R {\displaystyle R} 是地球半径， D {\displaystyle D} 是地心与月心的距离， θ θ --> {\displaystyle \theta } 是该单位质量与地心的连线与地—月连线的夹角。

最高潮发生在正面向月球 ( θ θ --> = 0 0 {\displaystyle \theta =0^{0}} ) 和正背向月球 ( θ θ --> = 180 0 {\displaystyle \theta =180^{0}} ) 两位置。在该两处 T v = 2 G m R D 3 {\displaystyle T_{v}={\frac {2GmR}{D^{3}}}} 及 T h = 0 {\displaystyle T_{h}=0} 。最低潮则发生在 θ θ --> = 90 0 {\displaystyle \theta =90^{0}} 和 θ θ --> = 270 0 {\displaystyle \theta =270^{0}} 两位置。在该两处 T v = − − --> G m R D 3 {\displaystyle T_{v}=-{\frac {GmR}{D^{3}}}} 及 T h = 0 {\displaystyle T_{h}=0} 。

数值上， T v = 2 G m R D 3 {\displaystyle T_{v}={\frac {2GmR}{D^{3}}}} 是地球引力加速度 g {\displaystyle g} 的千万份之一 ( 1 : 10 7 {\displaystyle 1:10^{7}} )。这个比例约莫等于一根火柴与一辆 2 公吨汽车重量之比。无论潮汐幅度如何，此垂直引潮力与海水的重量仍保持这比例 (因为它们均正比于质量)。 如此微弱的引潮力是不可能在 g {\displaystyle g} 的影响下能垂直把海水拉起或压下。

事实上，海洋潮汐的发生是引潮力的水平分量 ( T h {\displaystyle T_{h}} ) 起的作用，而不是垂直分量 ( T v {\displaystyle T_{v}} )。 譬如，在 θ θ --> = 90 0 {\displaystyle \theta =90^{0}} (低潮) 至 θ θ --> = 0 0 {\displaystyle \theta =0^{0}} (高潮) 的范围内， T h {\displaystyle T_{h}} 都是沿地球表面以单一相同方向作用这长达地球周界四份之一的海水。 如果以平衡潮理论来说，这样把海水水平挤压就会令海水的压强在这大范围内随 θ θ --> {\displaystyle \theta } 缓慢增加。同时，海水保持着平衡，海面下增大了的压强就会把海水水位推至适当高度，在正面向和正背向月球两位置，海水的压强最大，水位亦升得最高 (潮涨)。 T h {\displaystyle T_{h}} 与 T v {\displaystyle T_数量级} 虽属同数量级 (一样微弱) ，但只是前者能产生可观察的效果， 因为它不须与地心吸力抗衡及可以有长达 10 7 m {\displaystyle 10^{7}m} 的作用距离 。

如果以动力潮理论来说， T h {\displaystyle T_{h}} 亦较 T v {\displaystyle T_{v}} 重要， 它会把海水推动，形成潮流、潮波，把海水带向潮涨位置 。

规律

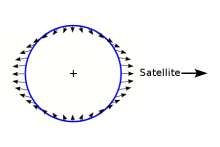
月球对地球不同部分的引力与对地心引力的差别

某个天体受外天体万有引力的作用下，正对外天体和背对外天体的部位向外凸出，而与外天体垂直的部位向内凹进。一般固体形变不明显，流体形变比较明显。

有关的学术文献多不胜数，计算潮汐高度的公式已广为人知。 。

影响

潮汐的存在使天体之间的相对速度减小，对彼此的自转起刹车作用。比如，月球和地球之间的潮汐使月球的自转周期等于它的公转周期，称之为潮汐锁定。

潮汐使天体被拉长，如果是黑洞等质量巨大的天体引起的潮汐，一旦潮汐力超过分子间作用力，会把周围的物体撕得粉碎。

虽然潮汐对固体形变的影响不大，但是潮汐往往成为地球上地震（星震）的诱因之一。

应用

水位的涨落形成了水的势能和动能，即潮汐能。潮汐能是一种蕴藏量大、洁净无污染的可再生能源。人们通常在潮汐能资源丰富的海湾或河口修建潮汐发电站，利用潮汐能发电。

对于以浮潜为玩乐的人士来说，涨潮时比退潮时更适合进行潜水活动。相反地，有些活动如挖蚬，退潮时比涨潮时更适合进行。

澎湖的双心石沪是利用海水的潮汐来捕鱼，当涨潮时，鱼会游进石沪里觅食，退潮后鱼就会受困在里面，这时渔民就可以趁机捕捞渔获。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。