联立多项式的零点

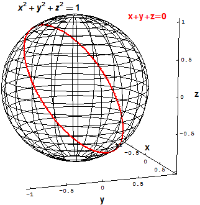
球和倾斜的圆周

在古典代数几何中，主要的研究对象是一组多项式的公共零点集，即同时满足一个或多个多项式方程的所有点组成的集合。 例如，在三维欧几里德空间 R 3 {\displaystyle \mathbb {R} ^{3}} 中的单位球面被定义为满足方程

的所有点 ( x , y , z ) {\displaystyle (x,y,z)} 的集合。

一个 "倾斜的" 圆周在三维欧几里德空间 R 3 {\displaystyle \mathbb {R} ^{3}} 中可以被定义为同时满足如下两个方程

的所有点 ( x , y , z ) {\displaystyle (x,y,z)} 的集合。

仿射簇

现在我们开始进入稍微抽象的领域。考虑一个数域 k ，在古典代数几何中这个域通常是复数域 C ，现在我们把它推广为一个代数封闭的数域。我们定义数域 k 上的 n 维仿射空间 A k n {\displaystyle {\mathbb {A} }_{k}^{n}} ，简单讲来，它只是一些点的集合，以下为方便我们简记为 A n {\displaystyle {\mathbb {A} }^{n}} 。

如果函数

可以被写为多项式，即如果有多项式 p 在

对 A n {\displaystyle {\mathbb {A} }^{n}} 上的每个点

都有

n 维仿射空间的正则函数正是数域 k 上 n 个变量的多项式。我们将 A n {\displaystyle {\mathbb {A} }^{n}} 上的正则函数记为 k [ A n ] {\displaystyle k[{\mathbb {A} }^{n}]} 。

与拓扑场论的关系

拓扑场论是数学物理中对sigma 模型（sigma model）的场做路径积分量子化的理论。

sigma 模型是从一个实二维曲面到一个固定空间的映射，再加上此二维曲面上一些丛的平滑截面。其中映射部分被称为玻色场（boson field），截面部分被称为费米场（fermi field）。该理论的主要目的是通过路径积分计算配分函数（partition function）。

在一些特殊情况下，可以用局部化方法把配分函数原在无限维空间的积分化简为在有限维空间的积分。对不同的作用量（action）而言，这个过程给出了代数几何的几种计数理论，包括：

Gromov Witten 不变量（即IIA型弦论）

辛流形里的全纯曲线计数

Seiberg Witten不变量

Chern Simon 数规范场

IIB型弦论则利用了 Hodge 结构的形变来计算。

注解

参见

参考书目

经典教科书，先于概形:

W. V. D. Hodge; Daniel Pedoe. Methods of Algebraic Geometry: Volume 1. Cambridge University Press. 1994. ISBN 978-0-521-46900-5.

Hodge, W. V. D.; Pedoe, Daniel. Methods of Algebraic Geometry: Volume 2. Cambridge University Press. 1994. ISBN 978-0-521-46901-2.

Hodge, W. V. D.; Pedoe, Daniel. Methods of Algebraic Geometry: Volume 3. Cambridge University Press. 1994. ISBN 978-0-521-46775-9.

不使用概形的语言的现代教科书:

Phillip Griffiths; Joe Harris. Principles of Algebraic Geometry. Wiley-Interscience. 1994. ISBN 978-0-471-05059-9.

Joe Harris. Algebraic Geometry: A First Course. Springer-Verlag. 1995. ISBN 978-0-387-97716-4.

David Mumford. Algebraic Geometry I: Complex Projective Varieties 2nd ed. Springer-Verlag. 1995. ISBN 978-3-540-58657-9. 引文格式1维护：冗余文本 (link)

Miles Reid. Undergraduate Algebraic Geometry. Cambridge University Press. 1988. ISBN 978-0-521-35662-6.

Igor Shafarevich. Basic Algebraic Geometry I: Varieties in Projective Space 2nd ed. Springer-Verlag. 1995. ISBN 978-0-387-54812-8. 引文格式1维护：冗余文本 (link)

关于概形的教科书和参考书:

David Eisenbud; Joe Harris. The Geometry of Schemes. Springer-Verlag. 1998. ISBN 978-0-387-98637-1.

亚历山大·格罗滕迪克.代数几何基础. Publications mathématiques de l"IHÉS. 1960.

亚历山大·格罗滕迪克.代数几何基础 1 2nd ed. Springer-Verlag. 1971. ISBN 978-3-540-05113-8. 引文格式1维护：冗余文本 (link)

Robin Hartshorne. Algebraic Geometry. Springer-Verlag. 1997. ISBN 978-0-387-90244-9.

David Mumford. The Red Book of Varieties and Schemes: Includes the Michigan Lectures (1974) on Curves and Their Jacobians 2nd ed. Springer-Verlag. 1999. ISBN 978-3-540-63293-1. 引文格式1维护：冗余文本 (link)

Igor Shafarevich. Basic Algebraic Geometry II: Schemes and Complex Manifolds. Springer-Verlag. 1995. ISBN 978-0-387-54812-8.

互联网上的资料:

Kevin R. Coombes:Algebraic Geometry: A Total Hypertext Online System

Algebraic geometryentry onPlanetMath

Algebraic Equations and Systems of Algebraic Equationsat EqWorld: The World of Mathematical Equations

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。