形成形成机制尚未明了，一般认为可能是由洋脊上不稳定处断开而产生的。不过2010年塔拉斯·戈亚（TarasGerya）的电脑模拟显示，转换断层是洋脊在扩张时于动态不稳定下渐渐弯曲而产生的。例子美国的圣安德烈亚斯断层（SanAndreasFault），位于陆地上的转换断层。中东的死海断层（DeadSeaTransformFault）新西兰的阿尔卑斯断层（AlpineFault）巴基斯坦的恰曼断层（ChamanFault）土耳其的北安那托利亚断层（NorthAnatolianFault）北美洲的夏洛特皇后断层（QueenCharlotteFault）

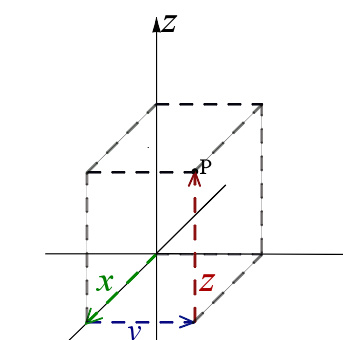
数轴数轴是最简单的坐标系，用一个实数标示一个点在线上的位置。数轴中会有一个原点O，以及单位长度及其方向。点P的坐标为从O到P的有号距离，坐标是正值或负值则依P点在原点的哪一侧来决定。数轴上每一个点都有唯一的坐标，每一个实数也都可以在数轴上找到唯一的对应点笛卡儿坐标系笛卡儿坐标系也称为直角坐标系，是最常用到的一种坐标系。是法国数学家勒内·笛卡尔在1637年发表的《方法论》附录中提到的。在平面上，选定二条互相垂直的线为坐标轴，任一点距坐标轴的有号距离为另一轴的坐标，这就是二维的笛卡儿坐标系，一般会选一条指向右方水平线称为x轴，再选一条指向上方的垂直线称为y轴，此两坐标轴设定方式称为“右手坐标系”。若在三维系统中，选定三条互相垂直的平面，任一点距平面的有号距离为坐标，二平面的交线为坐标轴，即可产生三维的笛卡儿坐标系。一般会选择x轴及y轴是水平的，z轴垂直往上，且三轴维持右手定则，若先将右手的手掌...

简介实投影平面可以看作是一个具有额外点的欧氏平面，这些点称之为无穷远点，并被认为是位于一条新的线上（该线称之为无穷远线）。每一个无穷远点对应至一个方向（由一条线之斜率给出），可非正式地定义为一个点自原点朝该方向移动之极限。在欧氏平面里的平行线可看成会在对应其共同方向之无穷远点上相交。给定欧氏平面上的一点(x,y)，对任意非零实数Z，三元组(xZ,yZ,Z)即称之为该点的齐次坐标。依据定义，将齐次坐标内的数值乘上同一个非零实数，可得到同一点的另一组齐次坐标。例如，笛卡儿坐标上的点(1,2)在齐次坐标中即可标示成(1,2,1)或(2,4,2)。原来的笛卡儿坐标可透过将前两个数值除以第三个数值取回。因此，与笛卡儿坐标不同，一个点可以有无限多个齐次坐标表示法。一条通过原点(0,0)的线之方程可写作nx+my=0，其中n及m不能同时为0。以参数表示，则能写成x=mt,y=−nt。令Z=1/t，则线上...

燃料热值和效率燃料的燃烧热可以以其HHV（高热值）或LHV（低热值）表示，高热值的燃烧热是在燃烧后，生成物的水蒸气已凝结成液态时的燃烧热，因此加上水凝结时的潜热。低热值的燃烧热则是在燃烧后，生成物的水蒸气仍维持气态时的燃烧热，不考虑水凝结时的潜热。燃料热值的选用会影响其能量转换效率的计算。在欧洲一燃料可产生的能量是其低热值表示，不考虑水凝结时的潜热，以若此方式计算冷凝式锅炉（英语：condensingboiler）的“热效率”，其数值可能会超过100%，其原因是其工作原理会利用到部分水凝结时的潜热，但计算输入能量时未考虑此部分所造成，不违反热力学第一定律。在欧洲以外的国家，一燃料可产生的能量是其高热值表示，已考虑水凝结时的潜热，以此为基础计算能量转换效率，其数字就不可能超过100%。不同能量转换方式的效率

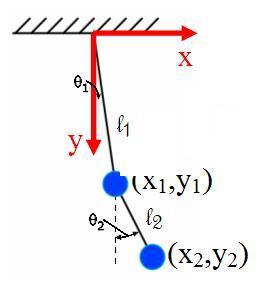
独立的广义坐标当分析有的问题时（尤其是当有许多约束条件的时候），最好尽量选择独立的广义坐标。因为，这样可以减少代表约束的变数。但是，当遇到非完整约束时，或者当计算约束力时，就必须使用关于这约束力的，相依的广义坐标。在三维空间里，假设一个物理系统拥有n{\displaystylen\,\!}颗粒子；那么，这系统的自由度是3n{\displaystyle3n\,\!}。再假设这系统有h{\displaystyleh\,\!}个完整约束；那么，这系统的自由度变为m=3n−−-->h{\displaystylem=3n-h\,\!}。必须用m{\displaystylem\,\!}个独立广义坐标(q1,q2,……-->,qm){\displaystyle(q_{1},\q_{2},\\dots,\q_{m})\,\!}与时间t{\displaystylet\,\!}来完全描述这系统的运...